Гидравлический расчет простого трубопровода

Задача 1. По трубопроводу диаметром D необходимо организовать перекачку жидкости на расстояние L. Удельная плотность и вязкость жидкости соответственно равны r и m. Начальный пункт трубопровода находится на высоте Z₁, конечный – на высоте Z₂. Давление жидкости в конечном пункте должно быть не менее P₂. Трубопровод длинный, величина местных сопротивлений составляет около 5% от величины линейных сопротивлений. Необходимо определить величину потерь напора на этом трубопроводе и давление жидкости в начальном пункте.

Решение. Так как весь трубопровод выполняется из труб одинакового диаметра, а жидкость несжимаема, то скорость жидкости на всех участках постоянна и равна

.

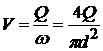Из формулы Дарси-Вейсбаха величина линейных потерь составит

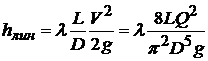
Коэффициент линейного сопротивления l зависит от режима течения жидкости. Вычислим значения критерия Рейнольдса по формуле

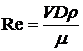
и определим значение l по кривой Никурадзе, аппроксимационным формулам или справочным таблицам.

Величина местных потерь ориентировочно равна

.

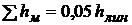Общая потеря напора в трубопроводе

.

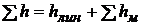Запишем уравнение Бернулли для начального и конечного пунктов:

.

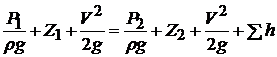Отсюда давление жидкости в начальном пункте трубопровода

.

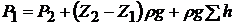В том случае, если режим течения соответствует квадратичной области и коэффициент гидравлического сопротивления не зависит от величины критерия Рейнольдса, методика расчета может быть несколько упрощена.

Обозначим

.

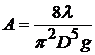Тогда формула Дарси-Вейсбаха примет вид

.

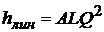Величину А называют удельным сопротивлением, она характеризует собой потери напора, приходящиеся на единицу длины трубы при единичном расходе, и имеет размерность [с/м³]². Произведение AL обозначают S и называют коэффициентом гидравлической характеристики трубопровода. Тогда

.

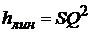Из формулы найдем выражение для расхода:

.

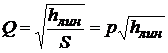Здесь 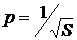- проводимость трубопровода.

Задача 2. Определить расход жидкости Q по трубопроводу длиной L, выполненном из труб диаметром D, если потери напора в трубопроводе составляют DН.

Решение. Так как коэффициент гидравлического сопротивления l зависит от скорости, которая в начальной стадии расчета неизвестна, то расчет выполняем методом последовательных приближений. Поскольку этот метод не дает абсолютно точного решения, то задаемся допустимой погрешностью расчета e, оценивающей степень расхождения одного из

Принимаем, что местные потери составляют 5% от общих потерь, откуда величина линейных потерь напора в трубопроводе равна

.

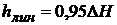Далее задаемся скоростью жидкости в трубопроводе, например, принимаем V₁ = 1 м/с. Затем вычисляем расход жидкости

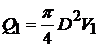
и определяем значение критерия Рейнольдса

.

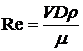и в зависимости от значения Re находим значение коэффициента гидравлического сопротивления l₁. Далее определяем величину потери напора, соответствующую принятой скорости V₁.

.

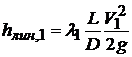После этого проверяем условие сходимости расчета

.

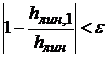Если это условие выполняется, то принимается, что расход жидкости 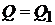и расчет заканчивается. Если расхождение велико, то расчет повторяется с новым значением скорости V₂. В качестве последующего приближения можно принять

.

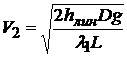Задача 3. Определить диаметр трубопровода длиной L, чтобы по нему перекачивать жидкость в количестве Q при потере напора DН.

Решение. Как и в предыдущей задаче, здесь не известна скорость жидкости и коэффициент гидравлического сопротивления l. Задаемся допустимой погрешностью e и в первом приближении принимаем 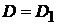. Затем определяем скорость жидкости в трубе по формуле

.

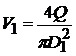Далее определяем значение критерия Рейнольдса

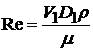
и находим значение коэффициента гидравлического сопротивления l₁. Как ранее, вычисляем линейные потери напора

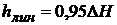
и рассчитываем эти потери соответственно диаметру D₁ по формуле

.

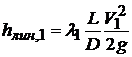Затем проверяем сходимость расчета по условию

.

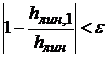Если это условие не выполняется, перезадаемся новым значением диаметра. Следующее приближение можно определить по формуле

.

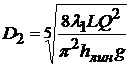После того, когда расчет сойдется, следует провести корректировку найденного диаметра. Для изготовления трубопроводов используются трубы стандартного диаметра, поэтому найденное значение диаметра следует увеличить до ближайшего стандартного значения.

Если трубопровод выполнен из труб различного диаметра, то расчет ведется для каждого из участков равного диаметра со своими значениями l. При этом общие потери напора складываются из потерь на участках.