Дифференцируемость функций многих переменных
Дифференцируемость функций многих переменных
Функция f называется дифференцируемой в точке 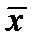 , если её полное приращение в этой точке может быть представлено в виде
, если её полное приращение в этой точке может быть представлено в виде 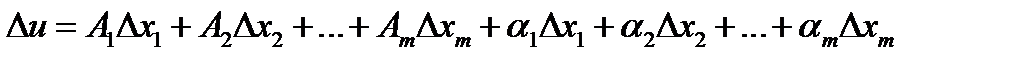 , где A1,A2,…,Am – числа, α1,α2,…,αm – бесконечно малые при
, где A1,A2,…,Am – числа, α1,α2,…,αm – бесконечно малые при 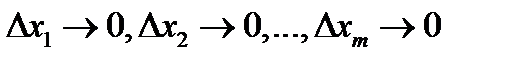 функции, равные 0 при
функции, равные 0 при 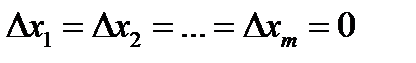 .
.
Достаточное условие дифференцируемости функций.
Если функция f имеет все частные производные в некоторой окрестности точки 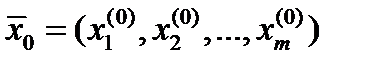 и все эти частные производные непрерывны в точке
и все эти частные производные непрерывны в точке 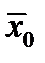 , то функция f дифференцируема в точке
, то функция f дифференцируема в точке 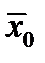 .
.
Достаточное условие локального экстремума
Пусть функция f – непрерывно дифференцируема в некоторой окрестности точки 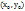 ,
, 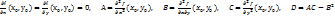 . Тогда: 1) если D>0, то функция имеет экстремум в точке
. Тогда: 1) если D>0, то функция имеет экстремум в точке 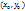 , а именно максимум, если A<0 (или C<0), и минимум, если A>0 (или C>0); 2) если D<0, то экстремума в точке
, а именно максимум, если A<0 (или C<0), и минимум, если A>0 (или C>0); 2) если D<0, то экстремума в точке 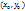 нет; 3) если D=0, то вопрос о наличии экстремума остается открытым.
нет; 3) если D=0, то вопрос о наличии экстремума остается открытым.
4. Теорема Больцана-Вейерштрасса.
Из любой ограниченной последовательности точек пространства 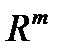 можно выделить сходящуюся подпоследовательность.
можно выделить сходящуюся подпоследовательность.
Теорема Кантора (непрерывность функции на компактном множестве)
Пусть 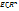 - компакт, и функция f непрерывна на Е. Тогда f равномерно непрерывна на E.
- компакт, и функция f непрерывна на Е. Тогда f равномерно непрерывна на E.
Теорема о независимости порядка дифференцирования
Если все частные производные порядка 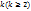 от функции f непрерывны, то в любой смешанной производной можно переставить порядок дифференцирования как угодно, не изменяя результата.
от функции f непрерывны, то в любой смешанной производной можно переставить порядок дифференцирования как угодно, не изменяя результата.
7. Критерий Коши́ сходимости векторных последовательностей
Для того чтобы последовательность имела конечный предел, необходимо и достаточно, чтобы она была фундаментальной.
Последовательность 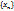 называется фундаментальной последовательностью, если для любого
называется фундаментальной последовательностью, если для любого 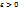 существует такой номер N>0, что для любых m>N,n>N выполняется d(xn,Xm)<
существует такой номер N>0, что для любых m>N,n>N выполняется d(xn,Xm)<  .
.
Необходимое условие дифференцируемости функций
Если функция f(x1,x2,…,xm) дифференцируема в  , то, а)она непрерывна в этой окрестности. б)Существуют частные производные
, то, а)она непрерывна в этой окрестности. б)Существуют частные производные 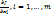 ; причём
; причём 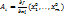 .
.
Необходимое условие локального экстремума
Если функция f достигает в точке 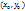 локального экстремума и имеет в ней частные производные первого порядка, то
локального экстремума и имеет в ней частные производные первого порядка, то 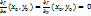 . Точка в которой обе частные производные равны 0, называется стационарной.
. Точка в которой обе частные производные равны 0, называется стационарной.
10. Определение компакта (компактного множества)
Множество 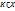 называется компактом, если из любого покрытия K открытыми множествами можно извлечь конечное подпокрытие.
называется компактом, если из любого покрытия K открытыми множествами можно извлечь конечное подпокрытие.
Определение частной производной
Если существует предел отношения 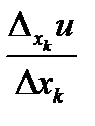 при
при 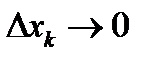 , то этот предел называют частной производной функции f в точке
, то этот предел называют частной производной функции f в точке 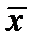 по к-ой переменной. Таким образом
по к-ой переменной. Таким образом 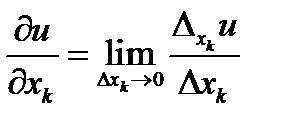 .
.
12. Определение функции многих переменных
Если каждой точке 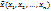 множества D ставится в соответствие единственное число у из I, то говорят, что задана функция n переменных у=f(x1, …, xn). Множество D называется областью определения функции D(у)=D, множество I называется множеством значений функции I (у)= I.
множества D ставится в соответствие единственное число у из I, то говорят, что задана функция n переменных у=f(x1, …, xn). Множество D называется областью определения функции D(у)=D, множество I называется множеством значений функции I (у)= I.
Определение первого дифференциала.
Дифференцируемость функций многих переменных
Функция f называется дифференцируемой в точке 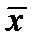 , если её полное приращение в этой точке может быть представлено в виде
, если её полное приращение в этой точке может быть представлено в виде 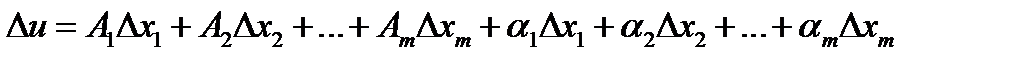 , где A1,A2,…,Am – числа, α1,α2,…,αm – бесконечно малые при
, где A1,A2,…,Am – числа, α1,α2,…,αm – бесконечно малые при 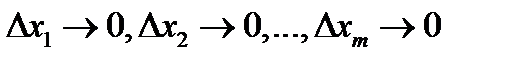 функции, равные 0 при
функции, равные 0 при 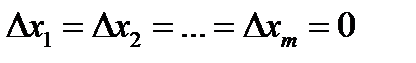 .
.
