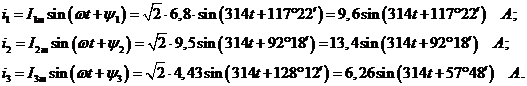Расчет мощностей и проверка правильности расчета мощностей токов при помощи уравнений баланса
Полные комплексные мощности источников эдс определяется по формулам
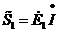 и
и 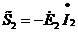
где 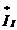 и
и  - сопряженные комплексы соответствующих токов. Знак "минус" в выражении
- сопряженные комплексы соответствующих токов. Знак "минус" в выражении 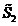 учитывает, что направления эдс и тока второго источника не совпадают.
учитывает, что направления эдс и тока второго источника не совпадают.
Итак, 
Отсюда мощности первого источника: 
полная 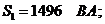
активная 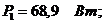
реактивная 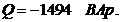

Мощности второго источника:

Знак "плюс" перед Р означает, что источник работает в режиме генератора и отдает в цепь активную мощность; знак "минус" означает, что источник работает в режиме потребителя и потребляет активную мощность. Знак "плюс" перед Q укалывает на то, что источник развивает (отдает в сеть) реактивную индуктивную мощность; знак "минус" - что источник отдает в сеть реактивную емкостную мощность. По результатам расчета мощностей источников можно сделать вывод, что оба источника являются генераторами активной мощности и отдают в цепь реактивную емкостную (источник EI) и реактивную индуктивную (источник Е2) энергии.
Активные и реактивные мощности пассивных элементов удобно рассчитывать по формулам соответственно

Здесь "плюс" соответствует индуктивному сопротивлению, а "минус" - емкостному. Рассчитаем эти мощности для исследуемой цепи:


Запишем уравнения баланса активных и реактивных мощностей цепи на основании закона сохранения энергии: алгебраическая сумма активных мощностей источников равна сумме активных мощностей, потребляемых всеми активными элементами цепи; алгебраическая сумма реактивных мощностей источников равна алгебраической сумме реактивных мощностей всех реактивных элементов цепи.
Для рассчитываемой цепи
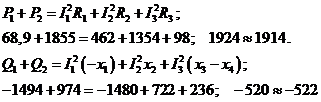
Co знаком "плюс" записываются индуктивные мощности, со знаком "минус" - емкостные. Выполнение этих равенств означает, что расчет выполнен правильно.
Максимально допустимая погрешность расчета 1 %.
Построение векторной диаграммы токов на комплексной плоскости
Комплекс каждого тока изображаем соответствующим ему вектором, длина которого равна действующему значению тока (модулю комплекса), а угол, образуемый им с положительным концом вещественной оси, равен начальной фазе тока (аргументу комплекса). Можно построить вектор по его проекциям на оси - действительной и мнимой частям, комплексной величины. На рис. 3.4 показана векторная диаграмма токов рассчитываемой цепи. При правильно выполненном расчете векторная диаграмма должна соответствовать, уравнению первого закона Кирхгофа (для узла цепи), т.е. 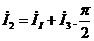

Рис. 3.4. Векторная диаграмма токов
Уравнения доя мгновенных значений токов
В результате расчета каждый ток получен в виде комплексов

где I - действующее значение тока;
ψ - начальная фаза.
Мгновенное значение тока имеет выражение
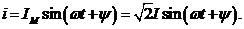
Таким образом,