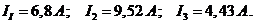Расчет токов в ветвях методом контурных токов
Задание на расчет цепи
По выданному преподавателем номеру варианта (№B) и значению К необходимо по табл. 1.1 данных указаний определить номер расчетной схемы (№cx) и вариант параметров схемы (№п), которые затем находят на рис. 3.1 и табл. 3.1 соответственно.
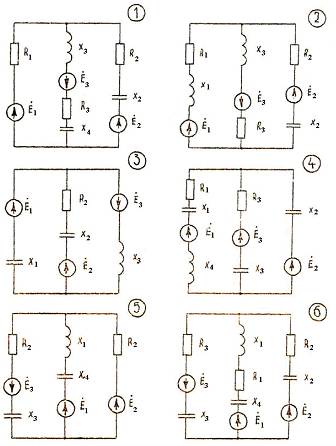
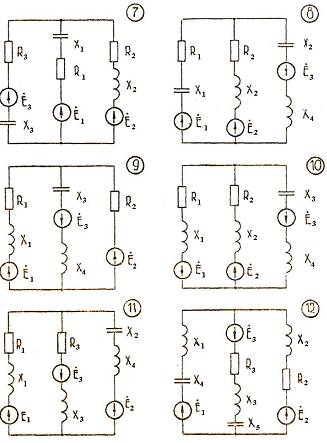
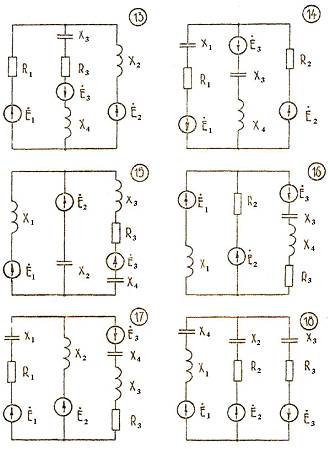
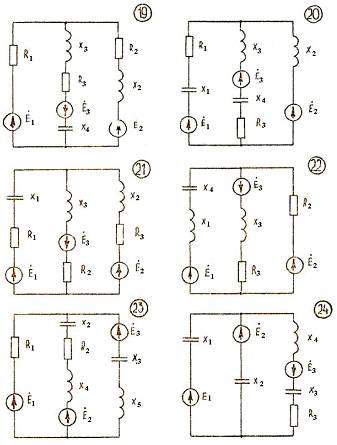
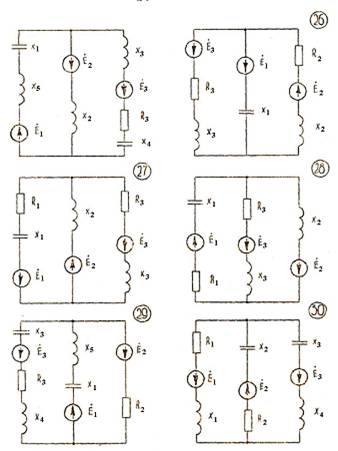
Рис. 3.1 Расчетные цепи (схемы) переменного тока
Таблица 3.1
Значения параметров цепи (схемы) переменного тока
| Параметры цепи | R1 | R2 | R3 | X1 | X2 | X3 | X4 | X5 |
| Ncx, Nn | Ом | Ом | Ом | Ом | Ом | Ом | Ом | Ом |
| 9 | 47 | 58 | 37 | 11 | 9 | 43 | 15 | 27 |
e1 = 310 sin 314t B; e2 = 310 sin (314t + 60°) B; e3 = 141 sin (314t -30°) B
Примечание. Отсутствующие в схеме варианта задания параметры цепи (хотя они и указаны в табл. 3.1) необходимо принять равными нулю.
Для заданной цепи (схемы) необходимо выполнить следующее:
1.Рассчитать токи в ветвях методом контурных токов.
2.Определить активные и реактивные мощности источников эдс и всех пассивных элементов цепи.
3.Проверить правильность расчета токов, составив уравнения баланса активных и реактивных мощностей цепи.
4.Построить векторную диаграмму токов на комплексной плоскости.
5.Записать уравнения для мгновенных значений токов.
6.Исключить один из источников в схеме, соединив накоротко точки, к которым он присоединялся.
7.В полученной простой цепи со смешанным соединением элементов рассчитать токи во всех ветвях символическим методом.
8.Определить активную, реактивную и полную мощности цепи, а также активные и реактивные мощности всех ее элементов.
9.Выполнить проверку расчета, составив уравнения баланса активной и реактивной мощностей цепи..
10. Рассчитать коэффициент мощности цепи (cosφ) и определить его характер (отстающий или опережающий).
Литература: [1, с. 79...126; 2, с. 72...107].
3.2. Примерный перечень вопросов для защиты задания
1. Дать определения синусоидальной величины и основных её параметров: амплитуды, начальной фазы, частоты, угловой частоты.
2. Почему действующее значение синусоидальной величины является её основной характеристикой?
3. Показать связь между синусоидальной величиной и изображающим её вектором и комплексом.
4. С какой целью синусоидальные величины изображают векторами и комплексными числами?
5. Что такое векторная диаграмма?
6. Можно ли на векторной диаграмме изображать синусоидальные величины, изменяющиеся с разной частотой?
7. Объясните, почему при постоянном напряжения включение в цепь конденсатора равносильно разрыву цепи, а при переменном напряжении ток через емкость проходит?
8. Почему индуктивности элементов цепи учитывают при расчете переменных токов и не учитывают при расчете постоянных?
9. Как учитывают емкости и индуктивности элементов при расчете цепей синусоидального тока?
10. Как определить сдвиг фаз напряжения и тока цепи (угол φ)?
11. Что характеризует коэффициент мощности (cos φ)? Почему на практике стремятся увеличить cos φ ?
12. Что понимают под активной, реактивной и полной мощностями цепи? Как они рассчитываются?
13. В каких цепях возникает резонанс напряжения (тока) и почему он так называется? Каково значение коэффициента мощности при резонансе и почему оно такое?
14. В чем сущность символического метода расчета цепей переменного тока?
Пример расчета цепи синусоидального тока
Для схемы рис. 3.2 заданы: величины эдс и параметры цепи
e1 = 310 ∙ sin(314 t + 30°) B; е2 = З14 sin (314 t - 60°) B;
RI = 10 Ом; R2 = 15 Ом; R3 = 5 Ом;
xI = 32 Ом; x2 = 8 Ом; x3 = 22 Ом; x4 = 10 Ом.
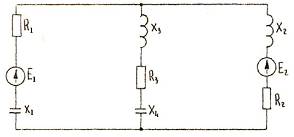
Рис. 3.2. Электрическая схема разветвленной цепи временного тока
Определение мощностей
Полная мощность (мощность на входе) равна мощности источника:
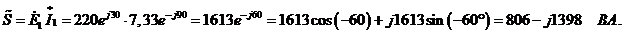
Мощности цепи равны

Мощности на элементах цепи:
активные реактивные
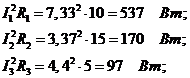
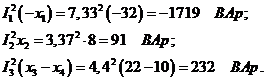
Коэффициент мощности цепи
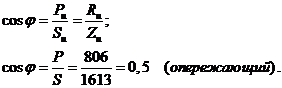
Коэффициент мощности можно определять другим способом. Аргумент полного комплексного сопротивления zвх равен сдвигу фаз тока и напряжения, т.е. φ . Следовательно, φ = -60ْ , cosφ = cos (-60 ْ ) = 0,5 (опережающий), т.е. источник эдс EI питает активно-емкостную нагрузку.
Задание на расчет цепи
По выданному преподавателем номеру варианта (№B) и значению К необходимо по табл. 1.1 данных указаний определить номер расчетной схемы (№cx) и вариант параметров схемы (№п), которые затем находят на рис. 3.1 и табл. 3.1 соответственно.





Рис. 3.1 Расчетные цепи (схемы) переменного тока
Таблица 3.1
Значения параметров цепи (схемы) переменного тока
| Параметры цепи | R1 | R2 | R3 | X1 | X2 | X3 | X4 | X5 |
| Ncx, Nn | Ом | Ом | Ом | Ом | Ом | Ом | Ом | Ом |
| 9 | 47 | 58 | 37 | 11 | 9 | 43 | 15 | 27 |
e1 = 310 sin 314t B; e2 = 310 sin (314t + 60°) B; e3 = 141 sin (314t -30°) B
Примечание. Отсутствующие в схеме варианта задания параметры цепи (хотя они и указаны в табл. 3.1) необходимо принять равными нулю.
Для заданной цепи (схемы) необходимо выполнить следующее:
1.Рассчитать токи в ветвях методом контурных токов.
2.Определить активные и реактивные мощности источников эдс и всех пассивных элементов цепи.
3.Проверить правильность расчета токов, составив уравнения баланса активных и реактивных мощностей цепи.
4.Построить векторную диаграмму токов на комплексной плоскости.
5.Записать уравнения для мгновенных значений токов.
6.Исключить один из источников в схеме, соединив накоротко точки, к которым он присоединялся.
7.В полученной простой цепи со смешанным соединением элементов рассчитать токи во всех ветвях символическим методом.
8.Определить активную, реактивную и полную мощности цепи, а также активные и реактивные мощности всех ее элементов.
9.Выполнить проверку расчета, составив уравнения баланса активной и реактивной мощностей цепи..
10. Рассчитать коэффициент мощности цепи (cosφ) и определить его характер (отстающий или опережающий).
Литература: [1, с. 79...126; 2, с. 72...107].
3.2. Примерный перечень вопросов для защиты задания
1. Дать определения синусоидальной величины и основных её параметров: амплитуды, начальной фазы, частоты, угловой частоты.
2. Почему действующее значение синусоидальной величины является её основной характеристикой?
3. Показать связь между синусоидальной величиной и изображающим её вектором и комплексом.
4. С какой целью синусоидальные величины изображают векторами и комплексными числами?
5. Что такое векторная диаграмма?
6. Можно ли на векторной диаграмме изображать синусоидальные величины, изменяющиеся с разной частотой?
7. Объясните, почему при постоянном напряжения включение в цепь конденсатора равносильно разрыву цепи, а при переменном напряжении ток через емкость проходит?
8. Почему индуктивности элементов цепи учитывают при расчете переменных токов и не учитывают при расчете постоянных?
9. Как учитывают емкости и индуктивности элементов при расчете цепей синусоидального тока?
10. Как определить сдвиг фаз напряжения и тока цепи (угол φ)?
11. Что характеризует коэффициент мощности (cos φ)? Почему на практике стремятся увеличить cos φ ?
12. Что понимают под активной, реактивной и полной мощностями цепи? Как они рассчитываются?
13. В каких цепях возникает резонанс напряжения (тока) и почему он так называется? Каково значение коэффициента мощности при резонансе и почему оно такое?
14. В чем сущность символического метода расчета цепей переменного тока?
Пример расчета цепи синусоидального тока
Для схемы рис. 3.2 заданы: величины эдс и параметры цепи
e1 = 310 ∙ sin(314 t + 30°) B; е2 = З14 sin (314 t - 60°) B;
RI = 10 Ом; R2 = 15 Ом; R3 = 5 Ом;
xI = 32 Ом; x2 = 8 Ом; x3 = 22 Ом; x4 = 10 Ом.

Рис. 3.2. Электрическая схема разветвленной цепи временного тока
Расчет токов в ветвях методом контурных токов
Предварительно представим эдс и сопротивления ветвей в комплексной форме:
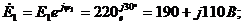

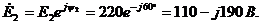
Здесь 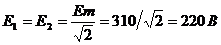 - действующие значение эдс.
- действующие значение эдс.
Комплексные сопротивления ветвей.
z1 = R1 – jx1 = 10 – j 32 = 33,5 · e-j72º39′ Ом;
z2 = R2 + j x2 = 15 + j 8 = 17ej28°04′ Ом;
z3 = R3 + j(x3 – x4) = 5 + j (22 – 10) = 13ej67°38′ Ом.
Эквивалентная расчетная схема представлена на рис. 3.3.
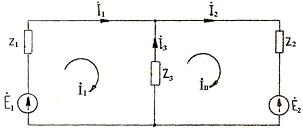
Рис. 3.3. Расчетная схема для МКТ
Схема имеет два смежных контура. Следовательно, по методу контурных токов нужно составить два уравнения. Зададимся произвольно направлениями контурных токов (в контурах удобно направлять их одинаково, например, по часовой стрелке) и составим для них уравнения по второму закону Кирхгофа:
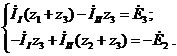
Здесь сопротивление первого контура
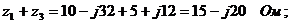
сопротивление второго контура
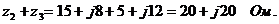
Сопротивление ветви, смежной для I-го и П-го контуров,
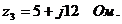
Подставляя значения сопротивлений и эдc в (3.1),получим
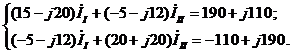
Систему уравнений (3.2) проще рассчитать на ЭВМ, пользуясь комплексом программ с комплексными коэффициентам (КС) (см. инструкцию с. З6 ).
Для расчета системы уравнений (3.2) с помощью программа "матрица", или используя комплекс программ с действительными коэффициентами (ДС), необходимо выполнить следующие алгебраические преобразования. Комплексы контурных токов запишем в алгебраической форме
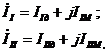
где IIд и IIIд - действительные составлявшие комплексов контурных токов 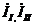 ;
;
IIM и IIIM - мнимые составляющие комплексов контурных токов. Подставим эти токи в систему уравнений (3.1), одновременно сделав подстановку числовых значений сопротивлений и эдс:
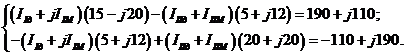 (3.3)
(3.3)
Раскроем скобки:
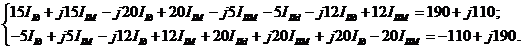
Далее, используя известное свойство комплексных чисел, - два комплексных числа равны, если соответственно равны их вещественные и мнимые части, - запишем систему уравнений в следующем виде:
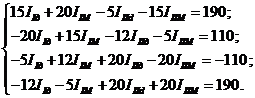
Для решения полученной системы уравнений на ЭBM составим матрицу из коэффициентов при действительных и мнимых составляющих токов и свободных членов. Матрица имеет вид
IIд IIM IIIд IIIM E
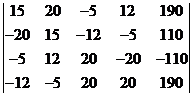 (3.6)
(3.6)
Введя матрицу в ЭВМ (см. инструкцию с. З6), получаем следующие результаты:
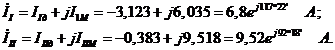
Действительные токи ветвей связаны с контурными токами следующим образом (см. рис. 3.3):
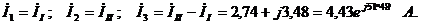
При определении тока 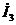 из большего по модулю контурного тока
из большего по модулю контурного тока 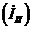 вычитаем меньший контурный ток
вычитаем меньший контурный ток 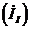 и направляем ток
и направляем ток 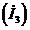 по направлению большего контурного тока
по направлению большего контурного тока 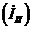 .
.
Действующие значения токов: