Системы эконометрических уравнений.

Рассмотрим методы анализа моделей, описывающих объекты, процесс формирования которых определяется системами взаимосвязанных соотношений. Такие модели называются системами эконометрических уравнений – СЭУ.

Для удобства переходят от переменных y и x к их отклонениям от средних, т.е.

, а свободные члены превращаются в ноль . Следовательно, уравнение приобретает вид:

Переменные, которые входят в эту систему называются: эндогенные – стоящие в левой чести (зависимые) и экзогенные – стоящие в правой части, а - параметры модел, которые подлежат оценке, 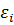– случайная ошибка.

Выбор метода оценивания параметра зависит от видов систем. Различают следующие виды систем:

Система независимых уравнений

1) Здесь предполагаем, что случайные ошибки удовлетворяют следующим условиям:
В каждом уравнении ошибки независимые, имеют нулевое математическое ожидание и одинаковую дисперсию:

2) Ошибки из разных уравнений системы не кореллированны:

, т.е.

При выполнении вышеуказанных условий, эконометрический анализ каждого уравнения системы может производиться независимо от остальных обобщенным методом наименьших квадратов.

1.2. Системы внешне не связанных уравнений – это система уравнений, в которой нарушено условие независимости случайных ошибок разных уравнений друг от друга.

, где , =1,2,…,

, где номер наблюдения

В связи с этим оценка параметров каждого уравнения в отдельности невозможно, потому что необходим совместный анализ таких уравнений.

, , , , =1,2,…,n

–вектор значений iой эндогенной переменной в каждом N наблюдении;
– матрица значений экзогенных переменных, включенных в iое уравнение системы;
- вектор неизвестных параметров iого уравнения;
- вектор ошибок iого уравнения.

или в матричном виде , где , , ,

Обобщенным методом наименьших квадратов мы можем оценить параметры этих моделей.

, где , где , – ковариационная матрица ошибок,

1.3. Системы рекурсивных уравнений– это системы эконометрических уравнений, в которых возможно упорядочить уравнения системы таким образом, чтобы в правой части первого уравнения присутствовали только экзогенные переменные , в правой части второго уравнения – только экзогенные переменные и всего одна эндогенная ( , в правой части третьего уравнения – только экзогенные и две эндогенные переменные , и т.д.

Если система такова, то эконометрический анализ каждого уравнения может производиться отдельно от остальных и параметры могут оцениваться с помощью обобщенного метода наименьших квадратов.

Система одновременных уравнений

Общая форма:

Приведенная форма – в правой части только экзогенные переменные: : , где - неизвестные параметры модели, связанные с предыдущими параметрами a и b.