Title ('Grow of the population')

В первой содержательной строке программы вводятся пределы интегрирования

уравнения [t(начальное), t(конечное)] и начальные условия по N для всех

рассматриваемых вариантов. Здесь приведен пример, в котором матрицы

параметра NChild и начальных условий интегрирования имеют размерность 7*1

(естественно, общую для них).

Для построения переходных процессов необходимо

- ввести или принять введенными значения параметров популяции NChild, Narс,

Commun, QLife, Contestв программе EL12maltode,

- затем ввести или принять введенными начальные условия и пределы

интегрирования в программе EL12grow,

- набрать в рабочем окне МАТЛАБ-а команду EL12grow.

Программа рассчитает и отобразит переходные процессы в популяции.

На Рис. 3 (а, б) эти процессы приведены для двух вариантов верхних пределов

интегрирования.

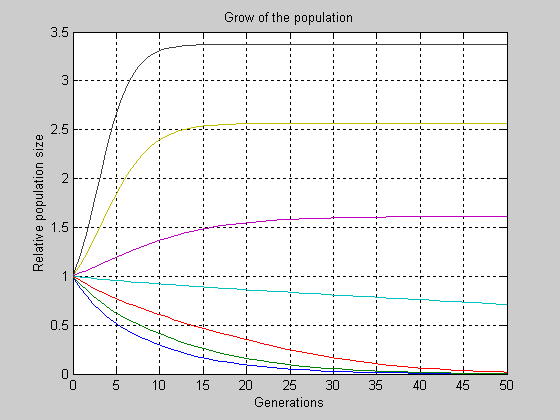
Рис. 3 а) Переходные процессы в популяции (вар. 1).

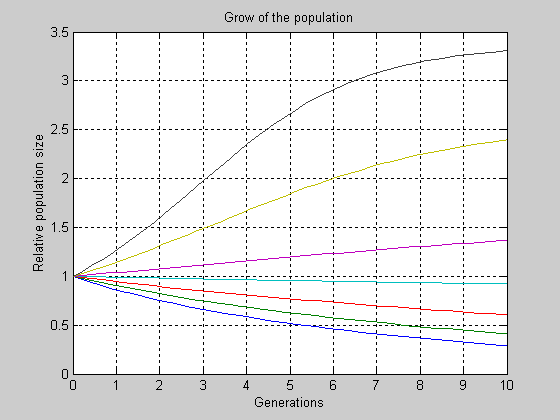
Рис. 3 б) Переходные процессы в популяции (вар. 2).

На переходных процессах наглядно отображено влияние параметра NChild на емкость ареала и время установления нового значения плотности популяции в нем при несбалансированных начальных условиях.

Характер этого влияния отобразите на приближенном графике.

Кроме того, проварьировав в программе EL12maltode остальные параметры популяции так же, как это делалось в предыдущем разделе для программы EL12Maltus , проделайте

следующее:

- считайте сграфиков переходных процессов их длительность T,

- заполните последний столбец таблицы 1,

- постройте соответствующие ему графики.

7. Анализ влияния наркотичности популяции на переходные процессы в ней.

- Возьмем за основу переходные процессы из предыдущего раздела работы и

введемстепень наркотичности популяции сначала Narc=0.1, затем Narc=0.2,

- и вновь построим переходные процессы.

Они приведены на фиг. 4 и 5, откуда видно, что при любых не только

реальных, но и завышенных значениях параметра NChild популяции с

наркотичностью такого уровня нежизнеспособны.

Из фиг. 6, где, в добавление к предыдущему случаю, построены переходные

процессы для случаев NChild=10 и NChild=15.

Видно, что лишь при чрезвычайно больших, нереальных значениях этого

параметра в популяции с высокой степенью наркотичности может наступить

стабилизация численности.

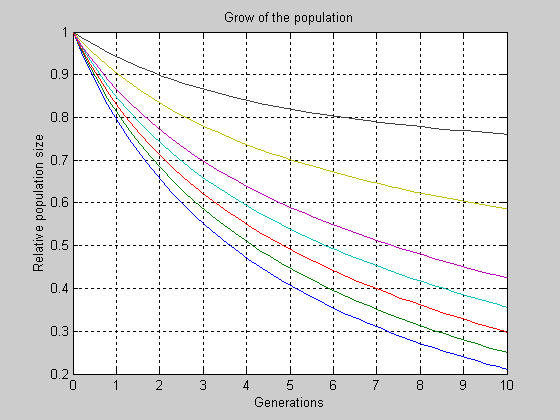
Рис. 4 Переходные процессы в популяции при степени ее наркотичности Narc=0.1.

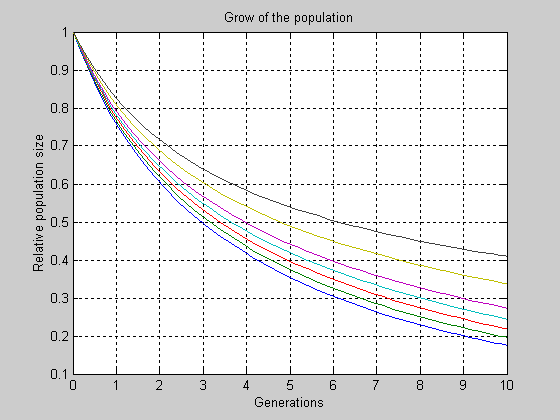
Рис. 5 Переходные процессы в популяции при степени ее наркотичности Narc=0.2.

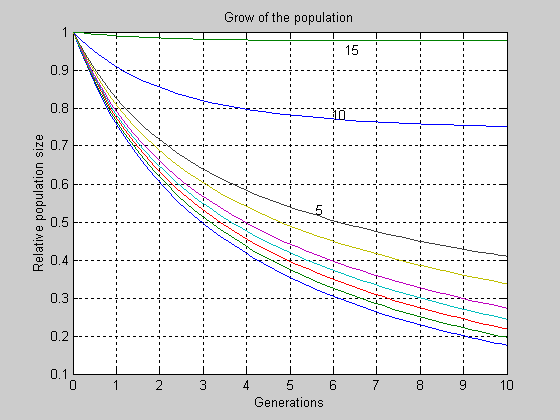
Рис. 6 Переходные процессы в популяции при степени ее наркотичности Narc=0.2.

В связи с актуальностью затрагиваемой проблемы рассмотрим ее несколько подробнее.

Методика определения границы устойчивости популяции.

Приняв за основу уже имеющиеся уравнения, найдем границу устойчивости популяции, то есть стабильности ее начальной относительной численности в плоскости параметров (Narc, NChild).

Решаемую задачу можно сформулировать так:

- построить функцию и (или) график, позволяющие определить, каким должно быть среднее

количество детей у сложившейся брачной пары в популяции, чтобы при любом заданном

уровне наркотичности популяции ее численность была стабильной, то есть производная от

численности была равна нулю.

Решение вопроса содержится в программе EL12narcborder, приведенной в приложении 4, с ее помощью построены графики, изображенные на Рис.7 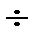10.

Кратко прокомментируем программу и графики.

За основу взят случай, ранее принятый за «стандартный», для него с помощью первой части программы построены функции рождаемости, смертности и мальтузианская (Рис. 7).

Рис. 7 Функции рождаемости, смертности и мальтузианская для популяции.

Заметим, что части программы разделены командой «pause», и для перехода от предыдущей части к следующей следует нажать на клавишу «ввод».

На графике виден промежуток положительности N’, следовательно, популяция способна к развитию. Из предыдущих графиков видно, что при больших значениях Narc она эту способность утрачивает.

В уравнениях (3 5) примем Increment=0 и разрешим их относительно NChild.

Получим

NCh=Death.*((.125*(1 - exp(-1*Commun*N))*exp(-7.6*Narc*N)*QLife).^(-1));

Приняв все параметры популяции, кроме Narc и NChild, стандартными и задав диапазон варьирования первого из них Narc=.00001:.001:.2, с помощью второй части программы построим график границы наркотической устойчивости численности популяции (Рис. 8).

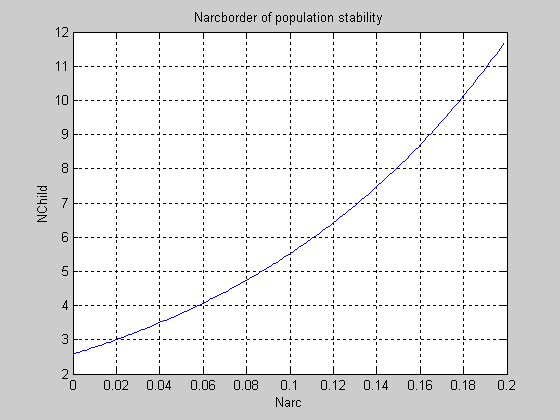
Рис. 8 Граница устойчивости популяции в плоскости двух параметров.

На двух последующих фигурах, построенных с помощью двух последующих частей программы, тот же график отображен в полулогарифмическом масштабе (варианты 1, 2),

с логарифмическим масштабом по одной из осей и линейным по другой, что позволяет более подробно увидеть его и начальный, и конечный участки.

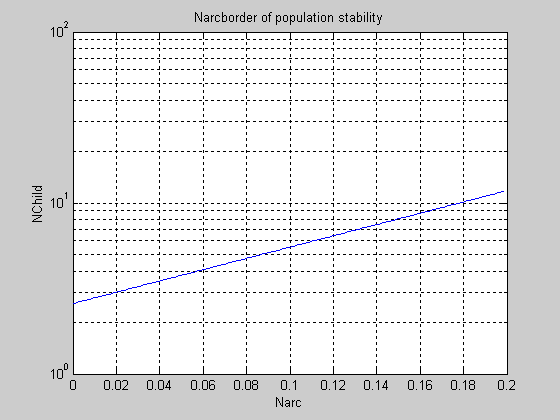
Рис. 9 Граница устойчивости популяции в плоскости двух параметров (вар. 1).

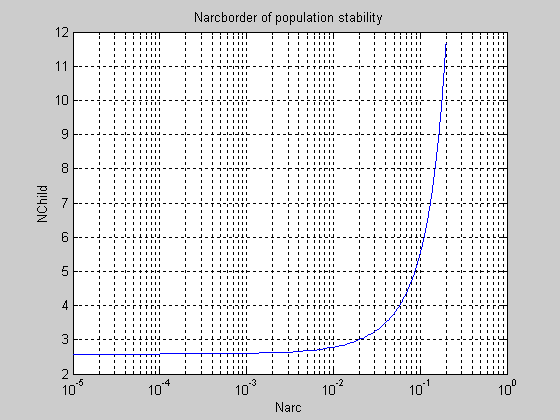
Фиг.10. Граница устойчивости популяции в плоскости двух параметров (вар. 2).

Приняв за норму, обеспечивающую сохранение популяции в условиях, близких к стандартным, значение NChild=2,5, можно считать, что для сохранения численности популяции в условиях ее наркотичности необходимо дополнительное среднее количество детей ∆NChild=NChild-2,5=F(Narc).

График этой функции, отстоящей на 2,5 единицы от границы устойчивости популяции, показан дополнительной (нижней) линией на фиг.11. Из него видно, что наркотичность популяции практически не может быть скомпенсирована каким-либо протекционизмом ее развития. Действительно, при Narc=0,1 такое компенсационное значение ∆NChild=3, а при Narc=0,2 имеем ∆NChild=9.

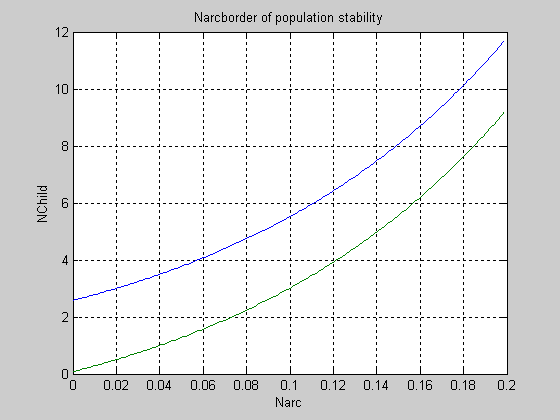
Рис. 11 Граница устойчивости популяции в плоскости двух параметров,

при ∆NChild=NChild-2,5=F(Narc) - нижняя линия.

Настоящий раздел является в основном ознакомительным и может послужить прототипом для самостоятельного инициативного исследования вопроса в других условиях

и при решении родственных задач.

8. Экспериментальное исследование чувствительности динамических свойств