Случайная величина, распределенная по нормальному закону, имеет математическое ожидание, равное 5, и среднеквадратическое отклонение, равное 15. Тогда ее функция распределения имеет вид

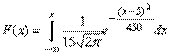
Случайным вектором или n-мерной случайной величиной называют

упорядоченный набор из n случайных величин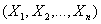

Среднеквадратическое отклонение дискретной случайной величины вычисляется по формуле

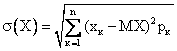
Станок-автомат производит изделия трех сортов. Первого сорта – 60 %, второго – 20 %. Вероятность того, что наудачу взятое изделие будет или второго, или третьего сорта, равна

0.40

Статистика 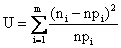, использующаяся в процедуре проверки гипотезы о виде распределения, имеет распределение

χ²

Статистика F, использующаяся в процедуре проверки равенства дисперсий двух генеральных совокупностей, имеет распределение

Фишера-Снедекора

Стационарными точками функции 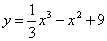являются точки с абсциссами

0, 2

Стационарными точками функции 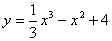являются точки с абсциссами (набрать числа в порядке возрастания через запятую в порядке возрастания)

0,2

Степенными функциями являются

,

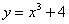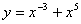
Страхуется 1500 машин. Вероятность попадания машины в аварию 0.15. При вычислении вероятности того, что число аварий не превысит 300, можно воспользоваться:

Интегральной формулой Муавра-Лапласа

Студент сдает два экзамена. Первый с вероятностью 0.8; второй – 0.7. Вероятность сдачи хотя бы одного экзамена можно вычислить следующим образом:

,

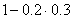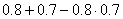
Студент сдает два экзамена. Первый с вероятностью 0.9; второй – 0.6. Вероятность сдачи хотя бы одного экзамена можно вычислить следующим образом:

,

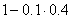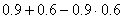
Сумма вероятностей 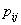, составляющих закон распределения двумерного дискретного случайного вектора, равна

Сумма квадратов отклонений S от точек (1,1), (1,3) (3,2), (3,4) до прямой y=x/2+1,5 равна (наберите число)

Тангенс угла наклона касательной к графику функции 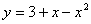в точке с абсциссой 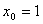равен (наберите число)

-1

Тангенс угла наклона касательной к графику функции в точке с абсциссой 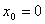равен (наберите число)

Тангенс угла наклона касательной к графику функции 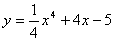в точке с абсциссой 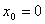равен (наберите число)

Тангенс угла наклона касательной к графику функции 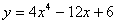в точке с абсциссой 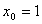равен (наберите число)

Термины "некоррелированные" и "независимые" случайные величины эквивалентны для случая

нормального распределения

Точечная оценка математического ожидания нормального распределения равна 11. Тогда его интервальная оценка может иметь вид

(10,1; 11,9)

Точечная оценка математического ожидания нормального распределения равна 12. Тогда его интервальная оценка может иметь вид...

(11,4; 12,6)

Точечная оценка математического ожидания нормального распределения равна 13. Тогда его интервальная оценка может иметь вид...

(12,3 ; 13,7)

Точка 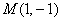для функции 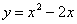является точкой

минимума

Точка с абсциссой 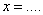для функции 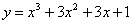является точкой перегиба (наберите число)

–1

Точкой перегиба функции 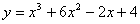является точка с абсциссой (наберите целое число)

-2

Точкой перегиба функции 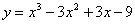является точка с абсциссой 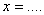^{(наберите число)}

Точкой перегиба функции 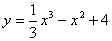является точка с абсциссой (набрать число)

Точкой перегиба функции 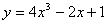является точка с абсциссой (набрать число)