Метод конечных элементов (МКЭ).

В методе Рэлея-Ритца координатные функции, определенные во всем теле, должны удовлетворять кинематическим краевым условиям, что для тел сложной формы сделать практически невозможно. Кроме того, матрица системы уравнений относительно коэффициентов при координатных функциях (обобщенных координат) оказывается полностью заполненной и, как следствие, плохо обусловленной.

В МКЭ используются простые (как правило, полиномиальные) координатные функции, определенные лишь в одной подобласти – в конечном элементе, а вне него равные нулю. Поэтому даже при одинаковой степени аппроксимации искомой функции в каждом из элементов координатные функции линейно независимы.

В качестве обобщенных координат принимаются значения искомой функции в некоторых точках на границе и внутри элемента (узлах) и координатные функции в конечном элементе называются функциями формы.

Рассмотрим в качестве примера элементы для одномерных задач.

1. Элемент первого порядка (линейная аппроксимация)

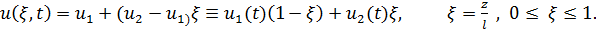
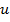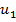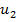2. Элемент второго порядка (квадратичная аппроксимация)

Квадратичная функция имеет вид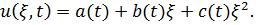

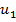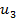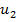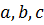Коэффициенты можно найти из системы

.

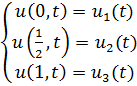На практике 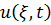записывают в виде

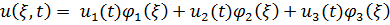, где функции формы должны удовлетворять условиям:

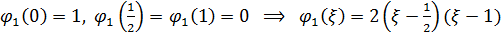
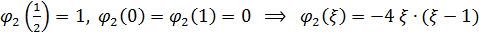
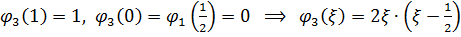
Пример 2. Продольные колебания консольного стержня постоянного сечения.

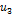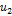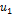(1)

(2)

Найдем матрицы инерции и жесткости для элемента первого порядка длиной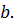

Имеем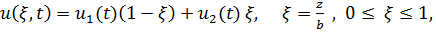

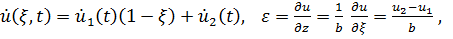
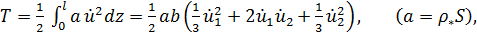
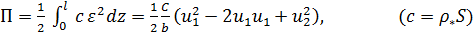
Разобьем стержень длиной 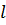на два элемента длиной 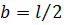и, складывая кинетические и потенциальные энергии элементов, получим с учетом выполнения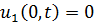

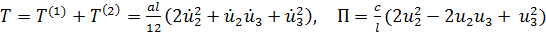
Уравнения Лагранжа имеют вид

.

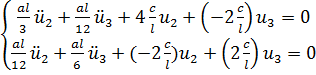Отыскивая решение в виде 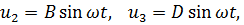получим

,

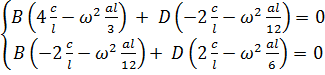и, приравнивая нулю определитель, получим частотное уравнение

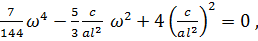
Откуда ,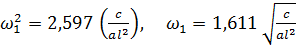

.

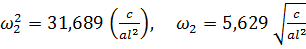Точные значения собственных частот равны

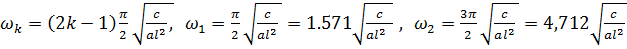
Первая собственная частота превышает точную на 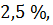вторая .

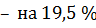В заключение заметим, что превышение приближенных значений собственных частот точных значений неслучайно – система с бесконечным числом степеней свободы всегда «мягче» построенных дискретизацией расчетных моделей.

Литература

1.Кочин Н.Е. Векторный анализ и начала тензорного исчисления. М.: Наука, 1965. 427с.

2. Маркеев А.П. Теоретическая механика. М.: Наука, 1990.414с.

3. Жилин П.А. Векторы и тензоры второго ранга в трехмерном пространстве.-

Санкт-Петербург, Изд-во «Нестор»,2001.275с.

4. Елисеев В.В. Механика упругих тел. СПб.: Изд-во СПбГПУ, 2003.336с.

5. Жилин П.А. Теоретическая механика. Фундаментальные законы механики:

Учеб. Пособие. СПб.: Изд-во СПбГПУ, 2003.340с.

6. Айзерман М.А. Классическая механика.- М., Наука,: 1974.367с.

7. Гантмахер Ф.Р. Лекции по аналитической механике.- М., Наука, 1966.

8. Бидерман В.Л. Теория механических колебаний: Учебник для вузов. -М.:

Высш.школа,1980. – 408с.

9. Тимошенко С.П. Колебания в инженерном деле. М., 1967.

10. Лурье А.И. Аналитическая механика. М.: ГИФМЛ, 1961. 824 с.