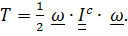Обобщенные координаты, связи, число степеней свободы.

Обобщенные координаты- параметры любой размерности 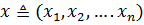, которые точно (либо с достаточной степенью точности) описывают положение тела.

Так, положение точки задается тремя координатами, твердого тела – шестью.

Обобщенными скоростями называются производные .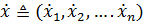

Ограничения, налагаемые на положения и скорости точек тела окружающими телами, называются соответственно позиционными (геометрическими) и кинематическими связями.

Связями называют и сами тела, обеспечивающие ограничения. Аналитические выражения, описывающие ограничения, называют уравнениями связей.

Если уравнения связей содержат только координаты, связи называются голономными; разумеется, голономными являются и интегрируемые кинематические связи.

Неинтегрируемые кинематические связи называются неголономными.

Число независимых обобщенных координат ( 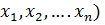называется числом степеней свободы по положению, а число независимых обобщенных скоростей – числом степеней свободы по скоростям. Рассмотрим некоторые простые примеры.

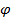x

X

Y

Z

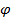X

Y

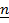1. Точка движется по поверхности

Три обобщенные координаты 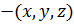, одно уравнение голономной связи(уравнение поверхности) 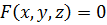, число степеней свободы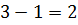

2. Качение диска.

Две обобщенные координаты 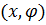, одно уравнение кинематической связи - условие отсутствия проскальзывания

.

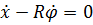Уравнение связи интегрируется: 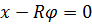, следовательно связь голономная и число степеней свободы .

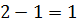3. Движение конька

Считаем, что лезвие конька касается льда в одной точке А и скорость точки касания направлена вдоль лезвия. Три обобщенные координаты ( 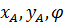), т.е. три степени свободы по положению; одна кинематическая неинтегрируемая, то есть неголономная связь - условие отсутствия бокового скольжения :

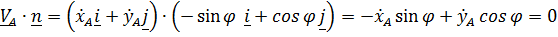
или .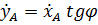

Таким образом, конек имеет две степени свободы по скоростям.

4. Изгиб стержня с шарнирными опорами.

Стержень - деформируемое тело с бесконечным числом степеней свободы. Для описания его изгиба можно взять в качестве обобщенных координат коэффициенты 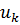в представлении 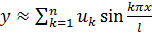, которое удовлетворяет краевым условиям – равенству нулю прогибов и моментов в шарнирных опорах. Разумеется, этот подход приближенный и соответствует описанию положения « с достаточной степенью точности».

6.2. Уравнения Лагранжа (второго рода).

Традиционно уравнения Лагранжа выводятся из уравнений Даламбера–Лагранжа для тел, состоящих из материальных точек, взаимодействие между которыми описываются только силами; хотя уравнения без какого–либо обоснования применяются для описания движения и твердых тел и твердых деформируемых тел, действие на тела–точки которых описывается силами и моментами, что влечет за собой необходимость введения наряду с возможными (виртуальными) перемещениями и возможных поворотов 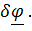Это нетрудно сделать только для плоских движений, когда 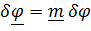, где единичный вектор m перпендикулярен плоскости движения.

Вместе с тем следует заметить, что принцип Даламбера, опирающийся на первый фундаментальный закон изменения импульса ( для точек–второй закон Ньютона) и на его обобщение для твердых тел-точек - на второй (закон изменения кинетического момента) требует введения совершенно новых понятий - возможных, виртуальных и действительных перемещений и поворотов. Подобный подход способен создать у изучающего механику впечатление, что, кроме фундаментальных законов, необходимы еще какие-то добавочные «принципы».

Мы покажем, что уравнения Лагранжа следуют из записанной в обобщенных координатах теоремы об изменении кинетической энергии, которая на основе первого и второго законов легко доказывается для систем, состоящих из материальных точек и твердых тел, воздействия на которые описываются силами и моментами; она же, разумеется , является частным случаем третьего фундаментального закона баланса энергии.

Принимается следующее утверждение: нестационарных связей в общепринятой со времен Лагранжа форме 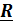= 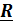(x, t) нет; явное присутствие времени в описании положения тела объясняется тем, что некоторые обобщенные координаты по необъясняемым причинам объявляются известными функциями времени.

Обозначим все обобщенные координаты (в том числе и зависимости которых от времени объявляются известными) через 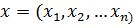.Линейные скорости и угловые скорости являются однородными линейными функциями обобщенных скоростей

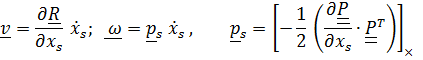
и, поскольку общий вид кинетической энергии для тел- точек имеет вид

T = 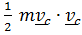+ 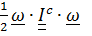, то кинетическая энергия всей системы будет однородной квадратичной формой обобщенных скоростей .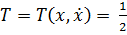

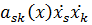Тогда .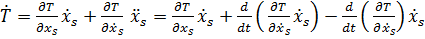

По теореме Эйлера об однородных функциях 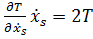, следовательно

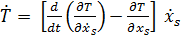
Мощность внешних и внутренних воздействий для тела-точки является однородной линейной формой обобщенных скоростей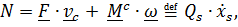

где коэффициенты при обобщенных скоростях по определению называются обобщенными силами. Теорема об изменении кинетической энергии 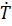= 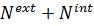принимает вид

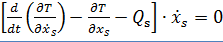
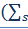!) ( 6.1)

Вследствие того, что теорема верна для всех движений, которые определяются произвольными начальными условиями и произвольными же обобщенными силами и из-за независимости обобщенных скоростей (для голономных систем) все коэффициенты при скоростях равны нулю:

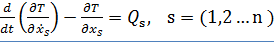( 6.2)

Это и есть система уравнений Лагранжа, которая определяет действительное движение.

На первый взгляд может показаться, что перечисленных факторов произвольности и независимости скоростей недостаточно, чтобы каждая из скобок в сумме

( 6.1) была равна нулю, поскольку внутри скобок имеются те же скорости.

Заметим, что уравнение ( 6.1) получено на основе первых двух фундаментальных законов, а внутри скобок стоят скалярные произведения уравнений этих законов на независимые для голономных систем базисные векторы 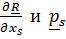множества векторов положения материальных точек и тензоров поворота твердых тел, входящих в систему.

Рассмотрим для простоты тело, состоящее из материальных точек. Умножим каждое уравнение скалярно на 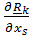и просуммируем их:

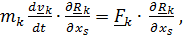
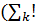), (s=1,2…n). ( 6.3)

Справа в ( 6.3) стоит обобщенная сила 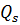, а левая часть стандартным образом (см. например 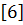) преобразуется с использованием тождеств Лагранжа, которые в нашем подходе ввиду отсутствия времени в описании положения 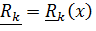совершенно очевидны ввиду независимости смешанных производных от порядка дифференцирования: ,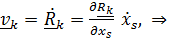

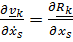и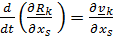

Имеем =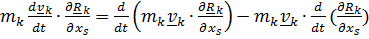

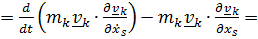
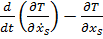, ( 6.4)

что и требовалось показать.

Такой же результат получим и для твердого тела, умножая уравнение второго закона :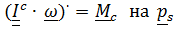

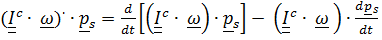. ( 6.5)

С помощью тождеств типа Лагранжа для вращательных движений

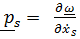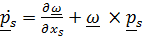, ( 6.6)

( 6.5) также приводится (см. приложение) к виду ( 6.4), где