Дифференциальные уравнения произвольного движения твердого тела. Замена опорной точки во втором фундаментальном законе.

Уравнения первого и второго законов полностью описывают трансляционное и вращательное движения твердого тела:

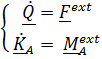. (5.31)

а)

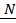• C

•B

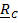A

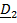• C

б)

Рис.5.4

B

Второму уравнению можно придать более удобный для решения вид.

Кинетический момент относительно неподвижной точки А можем выразить через кинетический момент относительно какой – либо подвижной точки В:

.

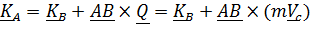Аналогично .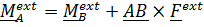

Подставляя эти выражения во второе уравнение (5.34), получим с учетом ,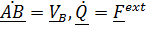

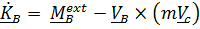. (5.32)

В некоторых случаях уравнение (5.32) проще и удобнее применять.

1. В качестве подвижной точки можем взять не принадлежащую телу точку, например, точку касания поверхности катящегося (или скользящего) тела.

.В этом случае 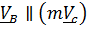, поэтому уравнение (5.32) упростится:

,

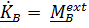и, кроме того, в уравнение не войдут неизвестные реакции, поскольку их момент относительно точки В равен нулю.

2. Если в качестве подвижной точки В взять центр масс, уравнение (5.32) примет вид

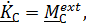
или, вспоминая что ,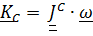

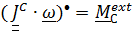. (5.33)

Это уравнение полностью описывает вращательное движение и не отличается от уравнения, описывающего вращение вокруг неподвижной точки.

Таким образом, удобной в большинстве случаев системой уравнений, описывающих произвольное движение твердого тела является

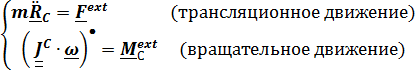(5.34)

Плоское движение.

Если тело совершает плоское движение, то 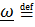. 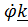, где 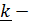единичный вектор, перпендикулярный плоскости движения.

X

Y

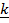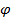С Z

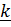Первое уравнение в (5.34) проецируется на оси X и Y в плоскости движения, а второе скалярным умножением на проецируется на ось Z , проходящую через центр масс:

.

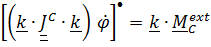С учето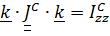м имеем

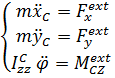(5.35)

Пример 1. Качение шара по вращающейся плоскости.

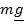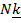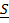𝜴

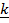• C

B

По вращающейся с угловой скоростью 𝜴 платформе катится шарик массы 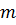и радиуса .

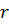Запишем уравнения динамики (5.34)

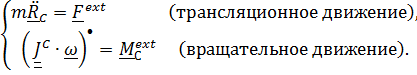
С учетом того, что тензор инерции шаровой 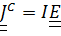, уравнения принимают вид

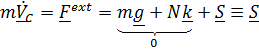, (1)

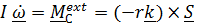, (2)

где 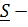горизонтальная составляющая реакции платформы.

Добавим к (1),(2) условие отсутствия проскальзывания в точке касания В:

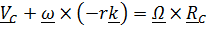(3)

Исключим из уравнений все неизвестные, оставив только 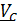.Подставим 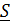из первого уравнения во второе, умножим его векторно справа на 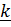и, раскрывая двойное векторное произведение, получим

.

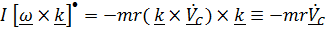Подставив в это уравнение найденное из (3) выражение 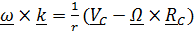, получим 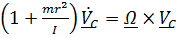или, обозначив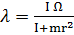

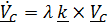
Подобное уравнение уже встречалось в (5.1.2) и решение его проще всего записать с помощью тензора поворота (напомним формулу Пуассона ):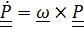

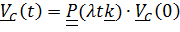
Таким образом, постоянный по величине вектор скорости «вращается» с постоянной угловой скоростью 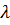вокруг 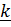; нетрудно понять, что это возможно, только если центр масс движется по окружности, радиус которой можно найти, если проинтегрировать 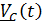и подставить начальные условия

Пример 2. Качение шара по внутренней поверхности вертикального цилиндра.

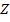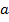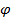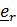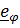Чтобы предотвратить проскальзывание, шарик массы m и радиуса 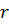катится с достаточно большой окружной скоростью. Кажется правдоподобным, что траектория будет иметь вид спирали увеличивающейся крутизны.

Скорость и ускорение центра масс шарика в цилиндрической системе координат

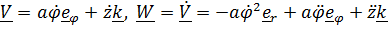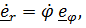
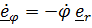, ( ). (1)

Уравнения движения

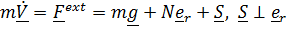, (2)

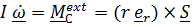, (3)

где 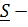лежащая в касательной плоскости в точке касания составляющая реакции.

Условие отсутствия проскальзывания

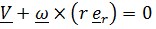, (в координатном виде 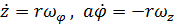) (4)

дополним его производной

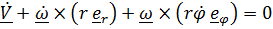. (5)

Выразим из (2) 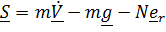, подставим его в (3) и найдем

.

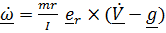Подставляя полученное выражение в (5), с учетом

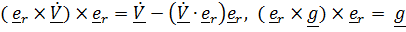
получим

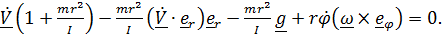(6)

Умножая скалярно уравнение (6) на 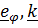,получим (проекция на 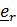равна нулю):

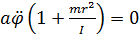(7)

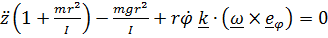(8)

Из (7) следует немедленно 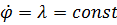, а в (8) величину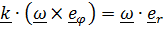

найдем через ее же производную: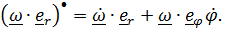

Первое слагаемое в силу (3) равно нулю, а второе с учетом (4) равно 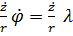, так что 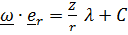(константу можем принять равной нулю). Окончательно получим

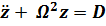,где обозначено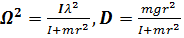

Решение этого уравнения имеет вид 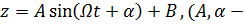постоянные, определяемые из начальных условий) и показывает, что шарик совершает гармонические колебания по высоте (!). Игрокам в гольф и баскетболистам не так уж «не везет», когда шарик (мяч) выкатывается из лунки (из кольца).

Динамические реакции оси вращающегося тела. Пример

Пусть твердое тело вращается вокруг неподвижной оси Z под действием момента 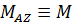. Поскольку нас интересуют только реакции, возникающие при вращении тела (динамические реакции) и которые, собственно, и принуждают тело совершать плоское движение, прочие воздействия не рассматриваются. Уравнения первого и второго законов имеют вид

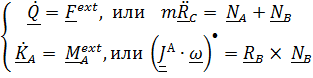(5.36)

Найдем проекции (5.39) на оси X,Y,Z, связанные с телом. Имеем

, , ,

,

,

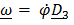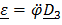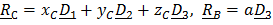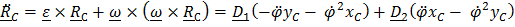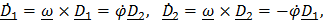
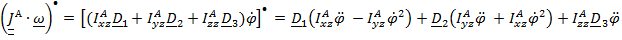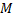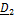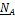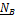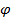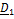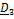C ·

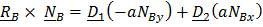
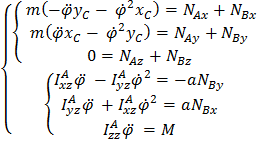(5.37)

Последнее уравнение – уравнение вращения вокруг неподвижной оси, третье уравнение содержит только сумму реакций, но не позволяет их найти. Первое, второе, четвертое и пятое уравнение – система, из которой определяются динамические реакции 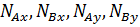и из нее же, разумеется, можем найти условия, при которых они равны нулю

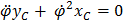
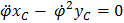
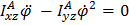
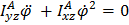
Так как движение произвольное, то выполнение этих равенств возможно только когда

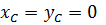- статическая уравновешенность и

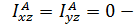динамическая уравновешенность,

т.е. динамические реакции равны нулю, если ось вращения является главной центральной.

Пример. Ось вращения диска составляет с перпендикуляром к плоскости диска угол 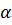. Диск статически уравновешен, т.е. центр масс лежит на оси вращения: 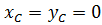. Масса диска 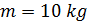, радиус 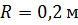, диск совершает 12000 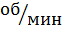, расстояние между подшипниками .

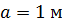A

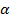BA

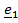C

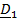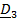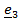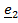Первые два уравнения системы (5.40) дают 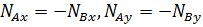, а из четвертого и пятого находим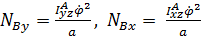

Центробежные моменты инерции найдем из теоремы Гюйгенса- Штейнера

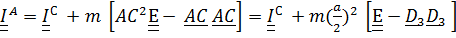, (1)

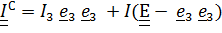, где .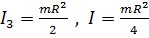

Из (1) имеем

,

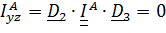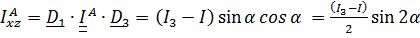
Таким образом, ,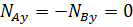

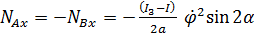
Для данных условий задачи и весьма незначительного угла 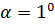получим

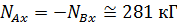, что значительно превышает статическую реакцию 5 кГ.