Маятник Фуко (точное решение линейной задачи)

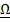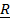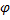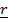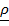Z

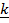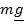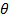Рассматривая движение маятника как сложное, состоящее из переносного вместе с Землей и относительного, запишем уравнение в виде

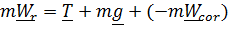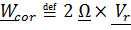, , или

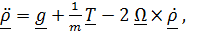где (1)

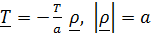, сумма 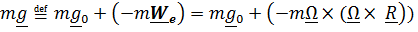–сила тяжести на данной широте .

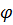Представим вектор угловой скорости Земли в виде 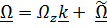и, удерживая линейные относительно 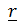( 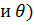величины, будем иметь

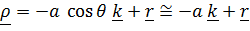, где 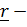горизонтальная составляющая вектора положения, ,

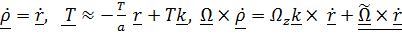где подчеркнутое слагаемое параллельно .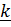

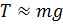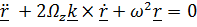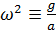Из проекции уравнения (1) на ось Z получим , а «плоская» часть примет вид , где . (2)

Решение уравнения (2) будем искать в виде 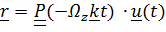. Используя формулу Пуассона 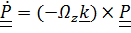, получим

,

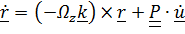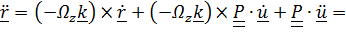
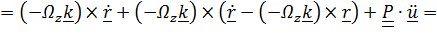
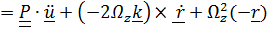, (учли, что ).

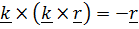Подставляя 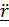в (2), получим 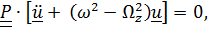или

.

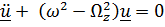Решение этого уравнения 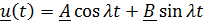, где 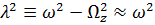, при произвольных 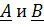, то есть при произвольных начальных условиях, описывает движение по эллипсу. Решение уравнения (2) 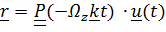описывает вращение этого эллипса по часовой стрелке с угловой скоростью 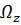. При начальных условиях, осуществленных Фуко (отклонение и отпускание без начальной скорости) 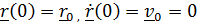находим 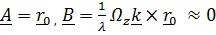и решение 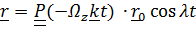можно трактовать как вращение плоскости колебаний маятника.

Пример 2. Отклонение снарядов (битва у Фолклендских островов).

В декабре 1914 г. произошло сражение между английской и немецкой эскадрами у Фолклендских островов( 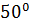южной широты).

По свидетельству английского морского офицера немецкие корабли обстреливались с максимальной дистанции (порядка 15 км), причем снаряды ложились левее цели примерно на сотню ярдов (примерно 90 м), хотя были пристреляны еще в Англии (примерно на 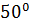северной широты).

Рассмотрим полет снаряда на широте .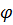

Z

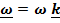Рис 5.2. Отклонение снаряда

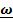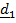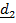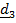X

Y

Z

Уравнение динамики относительного движения

,

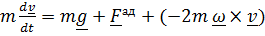где – скорость снаряда относительно Земли, 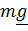- сила тяжести, считающаяся постоянной в рассматриваемой области, 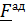- аэродинамическая сила.

Для простоты положим 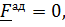тогда уравнение примет вид

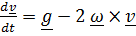. (1)

Это линейное дифференциальное уравнение может решено точно, мы построим здесь приближенное методом последовательных приближений.

Нулевое приближение получим, положив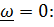

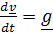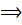
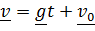, (2)

Первое приближение получим, подставив (2) в правую часть (1):

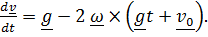
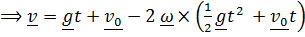. (3)

Если ограничиться линейными членами относительно малой величины 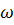( 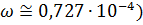, то этого приближения достаточно.

Сумма 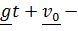это движение тела без учета вращения Земли, слагаемое

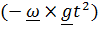объясняет отклонение падающих тел к востоку (в северном и южном полушариях). Слагаемое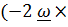 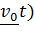описывает отклонение снаряда вправо от направления стрельбы в северном полушарии и влево в южном. Чтобы оценить это отклонение, будем считать для простоты траекторию настильной, т.е. 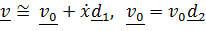. Проинтегрируем это слагаемое и найдем проекцию вектора положения на направление оси 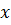(вправо от направления стрельбы):

.

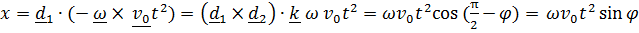В южном полушарии знак отрицательный, т.к. 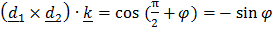, и снаряд отклоняется влево, поэтому при стрельбе в южном полушарии из орудия, пристрелянного в северном, отклонение удваивается.

Точное решение уравнения (1) в учебниках отсутствует; возможно, причина в громоздкости, если решать его в координатном виде. В векторном виде решение проще. Решение неоднородного уравнения 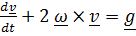равно сумме решений однородного уравнения 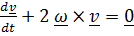и частного решения. Вспомнив формулу Пуассона (4.22)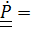 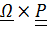, решение однородного уравнения немедленно запишем в ви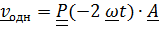де , где 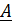- произвольный постоянный вектор. Частное решение найдем методом вариации произвольных постоянных:

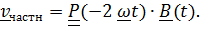
Подставив это выражение в уравнение, будем иметь

,

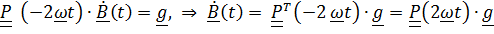откуда 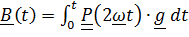(положили 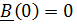и, следовательно, .

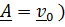. Записывая 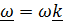и вспоминая представление Эйлера для тензора поворота

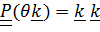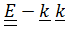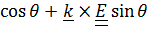+( ) , получим точное решение

.

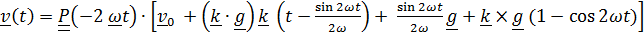Разлагая тригонометрические функции в ряды и, удерживая члены с первой степенью 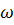, получим приближенное решение (3).

5.2. Второй фундаментальный закон механики - закон баланса момента количества движения (кинетического момента, момента импульса).