Связь тензора поворота и вектора конечного поворота .

В каком бы виде ни был записан тензор поворота – через направляющие косинусы или в виде композиции поворотов, угол поворота и ось поворота определяются из выражений для следа и векторного инварианта тензора поворота

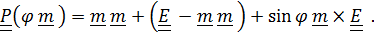
След и векторный инвариант равны

. (1)

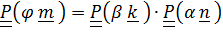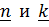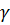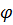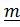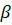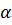Рассмотрим композицию поворотов вокруг осей, заданных единичными векторами , угол между которыми равен . Постараемся получить как можно более простые выражения для «суммарного» угла поворота и оси через углы и и оси 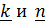. Перемножив тензоры и заменив в произведении диадные произведения скалярными и векторными, без труда найдем соответственно 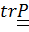и :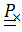

,

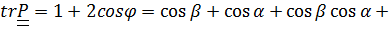
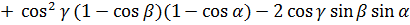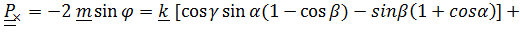
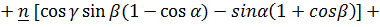
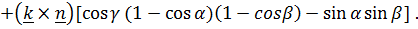
Эти выражения, приведенные в [3], можно упростить, заменив тригонометрические функции через половинные углы. Так, из выражения для 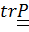имеем

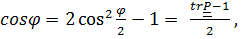откуда, опуская элементарные (хотя и громоздкие) выкладки, получим

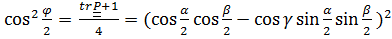или

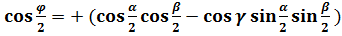.(2)

Аналогично, выражение для векторного инварианта преобразуется к виду

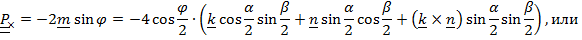
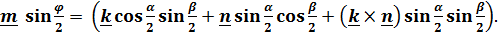(3)

Из системы уравнений (2), (3) определяются угол и ось «суммарного» поворота. Заметим, что знак (+) в (2) выбран из тех соображений, что если, например, 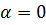, то угол 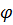должен быть равен другому: 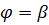и .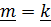

Если ввести векторы конечных поворотов Родрига

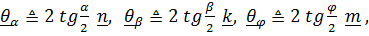
то уравнение (3) принимает форму правила сложения конечных поворотов [10]

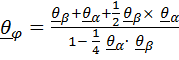
4.2.9.Сложное движение точки. Теоремы о сложении скоростей и ускорений (теорема Кориолиса).

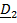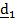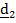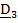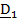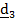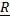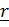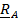S

Рис.4.15.

Имеются две системы отсчета - называемая неподвижной система S, в которой будут написаны все формулы, и подвижная 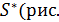4.15)

Движение точки по отношению к неподвижной системе называется абсолютным; скорость и ускорение обозначаются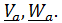

Движение точки по отношению к подвижной системе называется относительным; скорость и ускорение обозначаются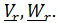

Движение подвижной системы по отношению к неподвижной называется переносным; скорость и ускорение того места подвижной системы, где в данный момент находится рассматриваемая точка, обозначаются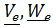

Вектор положения точки в неподвижной системе может быть представлен в виде суммы 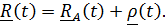Разложим 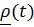по базису подвижной системы: ,

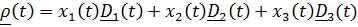где 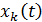– координаты относительного движения точки. Таким образом,

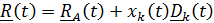(4.32)

Для упрощения записи формул ниже символ зависимости величин от времени опустим.

Дифференцируя (4.32) и заменяя по формуле Эйлера 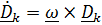, где 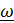– угловая скорость подвижной системы, получим

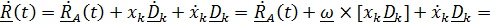
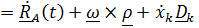(4.33)

Первые два слагаемых – уже знакомая скорость того места подвижной системы, где находится наблюдаемая точка, то есть переносная скорость

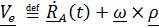, (4.34)

а сумма произведений производных относительных координат 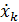на базисные векторы подвижной системы 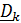является относительной скоростью:

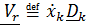. (4.35)

Таким образом, абсолютная скорость равна сумме переносной и относительной: 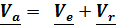.(4.36)

Продифференцируем (4.33): .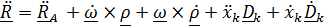

Подставив в это выражение 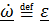- вектор углового ускорения подвижной системы, ранее полученную формулу (см. 4.33) 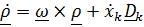,формулу Эйлера 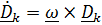,получим

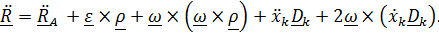
Первые три слагаемые - ускорение того места подвижной системы, где находится точка, то есть переносное ускорение

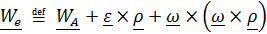, (4.37)

сумма произведений производных относительных координат 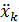на базисные векторы подвижной системы 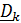является относительным ускорением

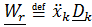, (4.38)

а последнее, далеко не очевидное слагаемое называется ускорением Кориолиса

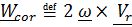. (4.39)

Получили теорему о сложении ускорений (теорему Кориолиса): Абсолютное ускорение равно сумме переносного ускорения, относительного и ускорения Кориолиса:

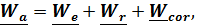(4.40)

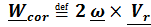
Замечание. Относительные скорость 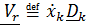и ускорение 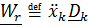обычно называют скоростью и ускорением, измеряемыми «подвижным наблюдателем», что не совсем верно, поскольку для подвижного наблюдателя подвижный базис 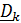является неподвижным 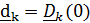, то есть «истинные» относительные скорость и ускорение равны 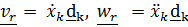, а 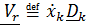и ускорение 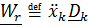- это повернутые вместе с подвижной системой «истинные».

Все вышеизложенное можно кратко получить, используя тензор поворота.

Вектор положения точки в неподвижной системе может быть представлен в виде суммы ,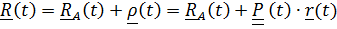

где 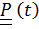-тензор поворота подвижной системы отсчета, 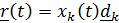– вектор в неподвижной системе, описывающий относительное движение, 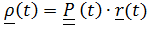- повернутый вместе с подвижной системой вектор 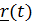, т.е это вектор относительного положения, каким его видит неподвижный наблюдатель (рис.4.14). Дифференцируя это равенство и воспользовавшись формулой Пуассона 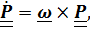получим теорему сложения скоростей

+ ,

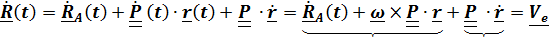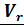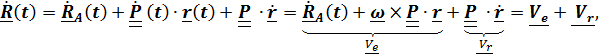
а дифференцируя еще раз – теорему о сложении ускорений

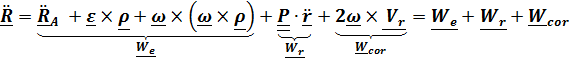
Сложное движение тела

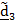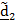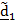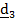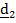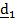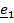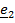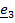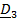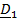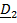Рис.4.16

Рассматривается движение тела («летающей тарелки») относительно двух систем отсчета - неподвижной с ортами 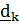и подвижной с ортами 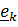(рис 4.16).

Необходимо определить абсолютную ориентацию тела по известной ориентации подвижной системы и относительной ориентации, информация о которой может быть передана в неподвижную систему любым способом, например, в виде телевизионной картинки или в числовом виде посредством направляющих косинусов 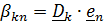, измеряемых подвижным наблюдателем.

Тензор поворота, описывающий «абсолютную» ориентацию 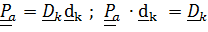; описывающий переносное движение 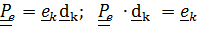. Тензор поворота относительной ориентации введем в виде 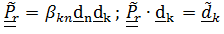, т.е. этот тензор действительно описывает то движение, которое «видит» подвижный наблюдатель, одушевленный или неодушевленный (например, телекамера) и которое неподвижный может наблюдать на экране телевизора. Таким образом,

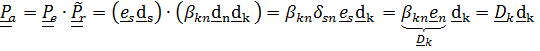(4.41)

Вектор угловой скорости по теореме о сложении угловых скоростей имеет вид

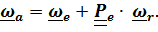(4.42)

Вектор углового ускорения

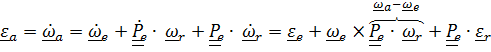, или

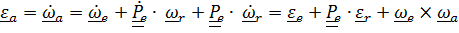(4.43)

Существует и другая [4] интерпретация сложного движения, которая в части описания ориентации по сути не отличается от вышеизложенного подхода, а вот в части определения относительной угловой скорости отличается существенно .

Тензор поворота переносного движения, как и ранее .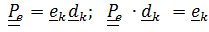

Тензором относительного поворота называется 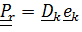; 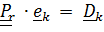.Действительно, матрица компонент этого тензора, записанного в базисе 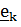, описывает относительную ориентацию .

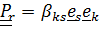Очевидно, что тензор поворота абсолютного движения

.

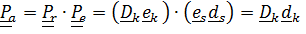Сразу же отметим, что 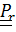- это повернутый вместе с подвижной системой «истинный» тензор поворота относительного движения :

,

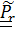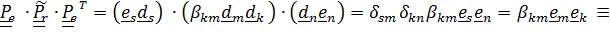
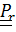так что 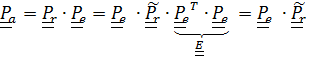– формула (4.41).

Векторы абсолютной и переносной угловых скоростей вводятся обычным способом в соответствии с формулой Пуассона 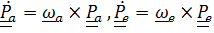, а вот вектор относительной угловой скорости 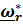определяется таким образом, чтобы формула сложения угловых скоростей имела привычный (см. любой учебник) вид

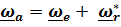. (4.44)

Для этого 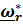вводится формулой

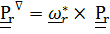, (4.45)

где 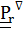- производная Яуманна, известная в теоретической механике как относительная производная. Так, если вектор задан координатами в подвижном базисе 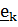, то полная производная по времени имеет вид

,

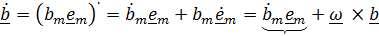где подчеркнутое слагаемое – относительная производная, т.е. производная, которую вычислял бы подвижный наблюдатель, для которого базисные векторы 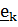неподвижны. Таким образом, .

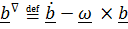Совершенно аналогично для тензора

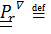
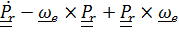. (4.46)

Дифференцируя 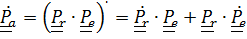и заменяя 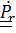по (4.46), (4.45), придем к (4.44).

Собственно говоря, из (4.42) следует, что 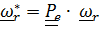, то есть это повернутый вместе с подвижной системой (вместе с телевизором ) «истинный» вектор угловой скорости относительного движения 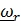. При графоаналитическом решении задач, когда, разумеется, рассматривается актуальное состояние, именно 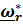изображается на рисунках.

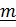В качестве примера можно рассмотреть, например, вращающуюся вокруг неподвижной оси с ортом платформу, относительно которой вокруг оси с ортом 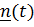вращается тело (см.рис.).

Введем подвижную систему отсчета, связанную с платформой.

. Тензор поворота переносного движения 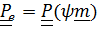. Тензор поворота относительного движения («истинный») 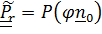, где 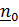- орт оси поворота тела в отсчетном положении. Заметим, что для подвижного наблюдателя постоянный вектор 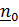остается неподвижным и впредь. Разумеется, по (4.41),(4.42)

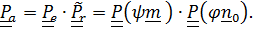(4.47)

.

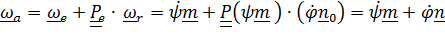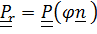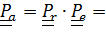
При втором подходе , , 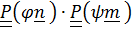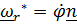(вектор 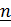считается постоянным). Так как 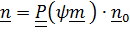, то по теореме (4.19) 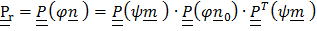и, как отмечалось выше, получим (4.47).