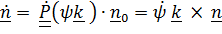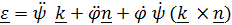Теорема о сложении угловых скоростей
Теорема. Если тензор поворота 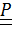 является композицией (произведением) поворотов
является композицией (произведением) поворотов 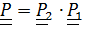 , то
, то 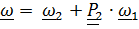 , (4.23)
, (4.23)
где 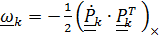 - угловые скорости, соответствующие тензорам
- угловые скорости, соответствующие тензорам 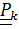 .
.
Доказательство. Докажем сначала лемму:
Пусть 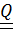 – тензор поворота,
– тензор поворота, 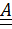 – произвольный тензор, тогда
– произвольный тензор, тогда
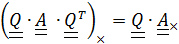 , (4.24)
, (4.24)
« векторный инвариант повернутого тензора равен повернутому векторному инварианту».
Доказательство леммы немедленно следует из тождества #3 (1.15)
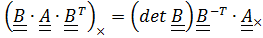 ,в котором достаточно положить
,в котором достаточно положить
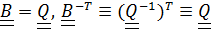 .
.
Впрочем, лемма имеет простой геометрический смысл. Примем в качестве 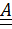 одну диаду
одну диаду 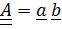 ( в лемму тензор
( в лемму тензор 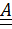 входит линейно). Пусть векторы
входит линейно). Пусть векторы
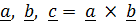 преобразуются тензором
преобразуются тензором 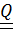 в
в 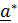 =
= 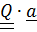 ,
, 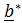 =
= 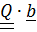 ,
, 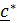 =
= 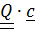 . Поскольку тройка поворачивается как жесткая система, то
. Поскольку тройка поворачивается как жесткая система, то 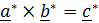 т.е.
т.е. 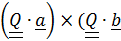 )=
)= 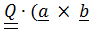 ) или
) или 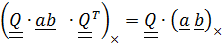 .
.
Вычисляя теперь тензор спина
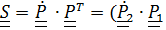 +
+ 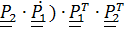 =
= 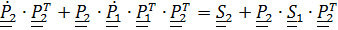
и сопутствующие векторы левой и правой частей с помощью леммы (4.24) получим (4.23).
Упражнение. Показать, что если 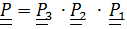 ,то
,то
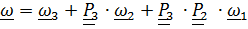
Дифференцируя (4.23), получим формулу сложения угловых ускорений
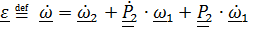 .
.
Заменив по формуле Пуассона 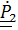 =
= 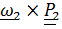 , будем иметь
, будем иметь
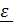 =
= 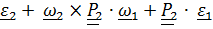 или, заметив, что
или, заметив, что 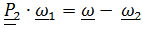
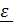 =
= 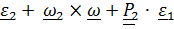 (4.25)
(4.25)
Замечание.
Практически во всех учебниках не дается строгого определения угловой скорости, это понятие остается затененным интуитивными соображениями (кроме случая фиксированной оси поворота, когда 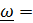
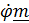 ). Доказываются «теоремы» о том, что
). Доказываются «теоремы» о том, что 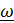 « можно переносить вдоль оси поворота», что угловые скорости можно складывать, если тело вращается вокруг параллельных, либо пересекающихся физических осей, но не рассматривается случай, когда оси не пересекаются и т.д. и т.п.
« можно переносить вдоль оси поворота», что угловые скорости можно складывать, если тело вращается вокруг параллельных, либо пересекающихся физических осей, но не рассматривается случай, когда оси не пересекаются и т.д. и т.п.
Теорема сложения угловых скоростей всегда приводится в виде 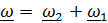 . Очевидно, что под
. Очевидно, что под 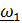 здесь понимается
здесь понимается 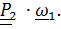
Примеры вычисления вектора угловой скорости.
Пример 1. Углы Эйлера
| Рис. 4.9. Углы Эйлера. |
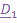 |
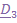 |
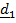 |
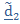 |
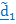 |
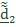 |
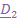 |
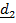 |
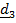 |
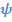 |
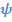 |
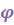 |
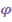 |
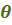 |
| Рис. 4.10. Углы Эйлера (волчок) |
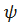 |
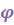 |
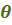 |
Традиционно углы Эйлера вводятся следующим образом. Переход из отсчетного положения
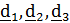 в актуальное
в актуальное 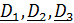 осуществляется тремя поворотами (рис.4.9):
осуществляется тремя поворотами (рис.4.9): 1. Поворот вокруг 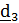 на угол прецессии
на угол прецессии 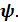 При этом
При этом 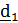 переходит в положение
переходит в положение
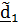 ,(
,( 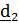 в
в 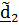 ). Этот поворот описывается тензором
). Этот поворот описывается тензором 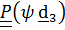
2. Поворот вокруг 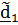 на угол нутации
на угол нутации 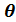 . При этом
. При этом 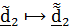 ,
, 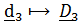 .
.
Этот поворот описывается тензором 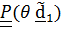
3. Поворот вокруг 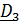 на угол собственного вращения
на угол собственного вращения 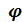 – тензор
– тензор 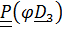 .
.
Таким образом, результирующий тензор поворота равен
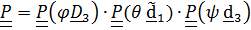 (4.26)
(4.26)
Для наглядности на рис.4.10 изображен волчок и углы Эйлера, описывающие его ориентацию.
Покажем, что традиционная последовательность поворотов (4.26) может быть заменена на последовательность поворотов на те же самые углы вокруг неподвижных осей:
1. Поворот вокруг 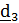 на угол собственного (чистого) вращения
на угол собственного (чистого) вращения 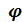
2. Поворот вокруг 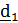 на угол нутации
на угол нутации 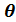 .
.
3. Поворот вокруг 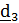 на угол прецессии
на угол прецессии 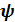
Поскольку 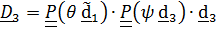 ,
, 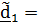
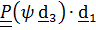 то по теореме (4.19)
то по теореме (4.19)
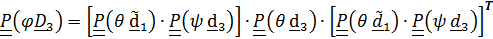 ,
,
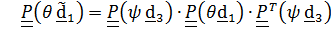 .
.
Подставляя эти выражения в (4.26), получим с учетом 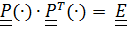
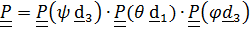 .
.  (4.27)
(4.27)
Разумеется, преимущество (4.27) по сравнению с (4.26) в том, что оси поворотов неподвижны.
Вектор угловой скорости по теореме о сложении угловых скоростей (4.23) равен
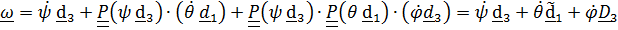 .
.
Это же (правильное) выражение обычно получают из (4.26), применяя правдоподобные рассуждения о сложении « бесконечно малых» поворотов; применив их к другой последовательности поворотов, например (4.27), получим абсолютно неверный результат 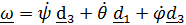 .
.
Из (4.27) видно, что при малом угле нутации 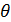 , когда
, когда 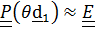 тензор поворота
тензор поворота
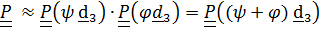 - углы
- углы 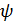 и
и 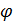 в линейном приближении становятся неразличимыми и входят в уравнения в виде суммы (
в линейном приближении становятся неразличимыми и входят в уравнения в виде суммы ( 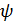 +
+ 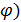 . В этом неудобство углов Эйлера.
. В этом неудобство углов Эйлера.
Пример 2. Самолетные (корабельные) углы.
Этого недостатка лишены самолетные (корабельные) углы (рис.4.11).
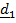 |
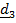 |
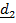 |
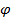 |
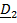 |
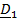 |
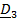 |
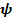 |
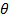 |
| Рис.4.11. Самолетные углы |
Переход из отсчетного положения 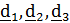 в актуальное
в актуальное 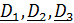 можно осуществить тремя поворотами (повернуть самостоятельно!) (рис.4.11):
можно осуществить тремя поворотами (повернуть самостоятельно!) (рис.4.11):
1. Поворот вокруг 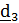 на угол рысканья
на угол рысканья 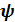 , при этом
, при этом 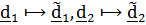
2. Поворот вокруг 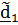 на угол тангажа
на угол тангажа 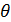 , при этом
, при этом 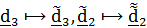
4.Поворот на угол крена 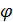 вокруг
вокруг 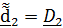 .
.
Тензор поворота равен 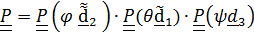 (4.28)
(4.28)
Выражение «можно осуществить» неслучайное; нетрудно понять, что возможны и другие варианты, например, повороты вокруг фиксированных осей. Применяя теорему о тензоре поворота с повернутой осью (4.19) из того, что 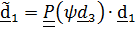 ,
, 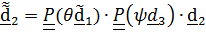 , будем иметь
, будем иметь
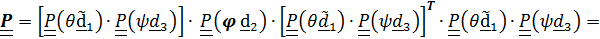
= 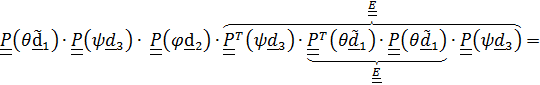
= 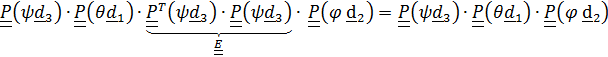 .
.
Таким образом, получили следующую композицию поворотов:
1. Поворот вокруг 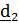 на угол крена
на угол крена 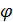 (рискуя сломать крылья)
(рискуя сломать крылья)
2. Поворот вокруг 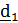 на угол тангажа
на угол тангажа 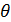 (подъем «носа»)
(подъем «носа»)
4. Поворот вокруг 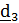 на угол рысканья
на угол рысканья 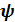
Тензор поворота и вектор угловой скорости имеют вид
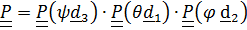 (4.29)
(4.29)
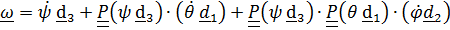
Пример 3. Трехстепенной гироскоп в кардановом подвесе.
| ротор |
 |
 |
 |
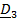 |
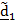 |
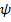 |
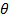 |
 |
| Рис.4.12. Трехстепенной гироскоп |
Карданов подвес имеет три физических оси поворота, поэтому нетрудно догадаться, как тремя поворотами вокруг неподвижных осей перевести ротор гироскопа из отсчетного положения в актуальное .Разумеется, последовательность поворотов может быть любой, но, как мы убедились, повороты вокруг неподвижных осей самые удобные.
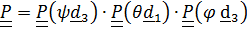 ,
,
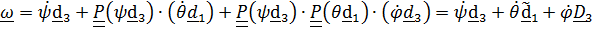 . (4.30)
. (4.30)
Физические оси позволяют правильно найти угловую скорость как сумму угловых скоростей вращений вокруг этих осей в актуальном положении.
Пример 4. Движение конуса по конусу
| D |
| Рис.4.13. Качение конуса(шестерни) |
 |
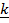 ψ ψ |
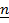 |
| α |
| βα |
| φ |
| b |
| K |
| A |
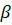 |
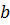 |
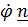 |
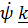 |
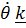 |
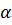 |
| Z |
| X |
| Y |
Ориентация подвижного конуса (шестерни) задается двумя углами – углом поворота
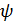 вокруг неподвижной оси (вектора
вокруг неподвижной оси (вектора 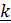 ) и углом
) и углом 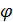 вращения вокруг собственной оси, актуальное положение которой задается вектором
вращения вокруг собственной оси, актуальное положение которой задается вектором 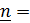
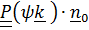 .
. Тензор поворота 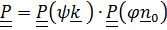 - повороты вокруг неподвижных осей.
- повороты вокруг неподвижных осей.
Вектор угловой скорости 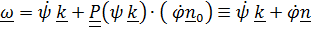 . (4.31)
. (4.31)
Если нет проскальзывания, то длина дуги окружности основания неподвижного конуса равна длине соответствующей дуги подвижного: 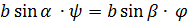 , откуда
, откуда 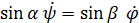 и
и 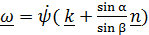 . Векторное произведение угловой скорости на вектор
. Векторное произведение угловой скорости на вектор 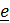 касающихся образующих конусов равно нулю:
касающихся образующих конусов равно нулю: 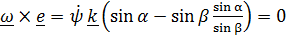 , следовательно,
, следовательно, 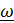 параллелен
параллелен 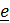 (см.рис.4.13).
(см.рис.4.13).
Впрочем, геометрическому подходу следует предпочесть кинематический. Так, если вращается и нижняя шестерня (конус), то для нахождения угловой скорости проще исходить из равенства скоростей в точке контакта К:
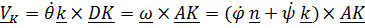 .
.
Проецируя эту формулу на ось 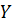 , получим
, получим 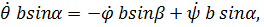
откуда 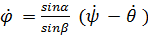 .
.
Дифференцируя угловую скорость (4.31), получим угловое ускорение
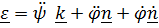 и с учетом
и с учетом