Вероятность символа и события в данном сообщении

Необходимо различать: а) вероятность сообщения или вероятность символа в данном сообщении; б) вероятность события, о котором сообщается. Гольдман[5] называет первое «языковой», второе – «семантической» информацией. Например, наиболее важные проблемы психологии мышления связаны с исследованием семантической информации.

В действительности как события, так и символы могут быть связаны. Например, в состав значащего слова данного языка нельзя включить никакие другие буквы, кроме некоторых определенных. Буквосочетание памя...можно дополнить буквами ть, ти, тью, но нельзя то, те, ты, тр и т.п. В буквосочетание понедель+икнельзя вместо знака + вставить никакую другую букву, кроме н. Это значит, что появление буквы н предрешено всей последовательностью букв данного слова, входящего в систему русского языка. Таким образом, необходимо учесть вероятность повторения связанной пары элементов всоставе сообщения, повторения тройки элементов и т.д. Макмиллан произвел подобное вычисление для английского языка. Оказалось, что если бы буквы появлялись с одинаковой вероятностью и независимо друг от друга, то на каждую из них приходилось бы 4,7 двоичной единицы информации. С учетом разновероятности 26 букв английского языка на каждую из них приходится 4,15 двоичной единицы, а с учетом частоты повторения групп по 8 букв – 2,35 двоичной единицы. Таким образом, информация как элемент сообщения ограничивается по мере увеличения вероятности появления сочетаний с возрастающим числом повторяющихся в определенном порядке элементов,

Отношение реальной неопределенности в алфавите букв данного языка (в английском – 2,35 двоичной единицы) к минимальной неопределенности, которая могла бы быть при том же числе букв (для английского языка log₂26=4,7), т.е. 2,35/4,10 1/2, называется относительной неопределенностью. Вычитая из единицы относительную неопределенность, определяют избыточность информации.

Избыточность информации

Понятие избыточности с успехом может быть применено к описанию ряда психологических явлений. Так, если речь руководителя рассматривать как некоторую систему сообщений, то всегда можно обнаружить ряд повторяющихся объяснений (пусть в разных вариантах слов) одного и того же явления, необходимых для усвоения подчиненными и закрепления знании. Такая избыточность увеличивает время прохождения темы, но вместе с тем увеличивает и надежность усвоения получаемой информации.

Для уяснения в общей форме самого понятия избыточности наметим некоторые пути его исследования.

Передаваемое в сообщении руководителя количество информации может быть найдено, если разработать технику расчетов согласно вышеуказанным принципам. Через опрос членов коллектива может быть определено и количество усвоенной информации. Тогда при однократном объяснении руководителя отношение этих величин может оказаться:

.

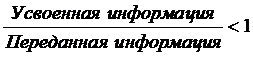Число дополнительных повторений для того, чтобы

.

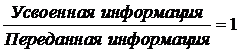будет давать меру необходимой (полезной) избыточности. Можно производить эти расчеты как в средних величинах, так и по отношению к любому члену коллектива, а также сравнивать индивидуальные отклонения от среднеквадратичного. В результате нетрудно выяснить, при каких способах повторения (вариации словесных формулировок и т.п.) достигается наилучший эффект. Конечная цель при решении этой задачи – поиск наиболее экономного и вместе с тем надежного способа передачи сообщений. В качестве наглядного примера приведем сравнение двух методов обучения грамоте; буквослагательного (путем называния букв – аз, буки, веди и т.п;) и звукового аналитико-синтетического. Очевидно, что методические приемы в первом случае обладают значительно большей избыточностью, чем во втором. Однако не всегда бывает ясно, какие из применяемых и предлагаемых сейчас методических средств являются оптимальными.

Избыточность передаваемого сообщения (как в вышеприведенном примере) всегда уменьшает количество информации, приходящейся на сигнальный элемент. Если же избыточность появляется на приемном конце как особенность самого приемного устройства, то количество информации на элемент сообщения увеличивается, Это реально выражается в том, что для ввода всего ансамбля элементов достаточен прием лишь некоторых из них. Данное явление в психологии известно под названием целостного восприятия.

В таком случае для узнавания какого-либо человека (или вещи) нет необходимости по отдельности и последовательно опознавать каждый элемент воспринимаемого, например глаза, нос, брови, ресницы, уши, ноги, руки и т.п. Объект в целом узнается по ограниченному числу взаимосвязанных элементов. Узнать знакомого можно по спине или профилю, по голосу или походке.

Наиболее отчетливо избыточность восприятия обнаруживается при обучении чтению, так как в процессе овладения этим навыком слова текста все легче узнаются по общему ансамблю последовательности элементов.

Всякая система, как сенсорная, так и моторная, если она сложилась, обладает избыточностью. Известно, что r такой системе, как динамический стереотип, прием одного элемента вызывает запуск всей последовательности элементов стереотипа. Важно раскрыть возможности положительных качеств избыточности. Психология заинтересована в том, чтобы узнать, какая именно по качеству информация передается тем или другим элементом сигнала. Решение этого вопроса позволяет вскрыть аналитико-синтетическую деятельность мозга в процессе не только приема, но и выдачи информации.

Психологию интересует канал информации от уха и глаза, вообще от рецепторов до мозга и от него до эффекторов. Особое внимание привлекают исследования центральных процессом в источнике и приеме информации. Это и есть проблема мышления и общения.

Информационная емкость

Пусть алфавит данного множества дискретных сообщений состоит из т символов, а разрядность сообщений – из n позиций. Будем рассуждать так. Если наше множество сообщений имеем алфавит m и разрядность n=1 (т.е. каждое сообщение этого множества состоит из одной позиции), то любое наугад выбранное из него сообщение будет состоять из одного из символов алфавита /н, занимающего и ли ни ионную позицию сообщения. Очевидно, всего будет т таких однопозиционных сообщений.

Если множество имеет алфавит т и разрядность n=2, то каждое сообщение этого множества будет иметь две позиции и, следовательно, число возможных сообщений в нем будет N = m×n = m².

В общем случае, когда сообщения множества имеют алфавит т, разрядность п и вероятность появления в любой позиции « каждого из символов т алфавита одинакова, будем иметь: N = mⁿ.

Это – число возможных сообщений в рассматриваемом множестве, определяющее информационную емкость или максимально возможное число сообщений, которые способна выдать, передать или хранить в себе система, оперирующая алфавитом из т символов и разрядностью из n позиций.

Такой системой может быть источник сообщений, канал связи или запоминающее устройство.

Пример 2.

Пусть m = 30 букв. Из них можно составить 30¹ = 30 однобуквенных слов (n = 1), 30² = 900 двухбуквенных (n = 2),30³ = 27000 трехбуквенных (n = 3), 30⁴ = 81000 четырехбуквенных (n = 4) и т.д. Между тем в действительности язык содержит примерно 50000 слов.

Информационную емкость принято, однако, оценивать логарифмом числа возможных сообщений: Q = log₂N log₂mⁿ = nlog₂m.

Применение логарифмической меры для измерения объемов информации и других измерений количеств информации оправдано тем, что она обладает рядом преимуществ, делающих удобными математические расчеты, в частности, математическим свойством аддитивности, благодаря которому, например, объемы информации различных источников сообщений могут суммироваться.

Так, если мы имеем два источника сообщений с емкостями Q₁ = n₁log₂m₁ и Q₂ = n₂log₂m₂, то при этом общий объем информации Q = Q₁ + Q₂ = n₁log₂m₁ + n₂log₂m₂

Пример 3.

Вычислим информационную емкость обыкновенного чистого листа бумаги, предназначенного для напечатания текста на научную тему. Будем считать, что с учетом пробелов между словами на таком листе помешается 2000 знаков. Следовательно, разрядность n = 2000 позиций. Далее, пусть алфавит текста включает: русский алфавит m₁ =32, латинский алфавит т₂=21, знаки препинания m₃=12, цифры т₄=10, арифметические знаки m_s=5. Отсюда находим «научный» алфавит: т= m₁ + m₂ + m₃ + m₄ + m₅ =32 + 27 + 12 + 10 + + 5 = 86 символов.

Информационная емкость нашего листа Q = nlog₂m = 2000 Iog₂86= 2000×6,5 = 13000 дв. ед.

Информационная емкость показывает, какое предельное количество информации может хранить, выдать или передать система, если она обладает конкретным алфавитом в т символов и разрядностью в n позиций.

Энтропия

Понятие «энтропия» введено в 1865г. Р.Клауэиусом. Статистическая физика рассматривает энтропию как меру вероятности пребывания системы в данном состоянии. Этим понятием широко пользуются в физике, химии, биологии и теории информации.

Энтропия (неопределенность) события, явления, процесса в полной мере существует только до получения сообщения или в общем случае – до проведения опыта. После получения сообщения (выполнения опыта) она исчезает или уменьшается, так как уже имеется определенная информация.

Если принять, что до получения информации существовала энтропия Н', а после получения информации она уменьшилась до величины Н", то количество полученной информации будет: DН = Н' – Н".

Если в результате получения информации полностью устранена неопределенность, то DН = Н', т.е. количество информации и в этом случае численно равно энтропии, имевшей место до получении информации. Чем в большей степени устранена неопределенность, тем больше полученная информация. Количественное равенство информации и первоначальной энтропии, конечно, не означает тождественности этих понятий. Более того, они противоположны друг другу, ведь информация равна ycтраненной энтропии.

Понятие энтропии применимо не только к сообщениям, но и к их источникам. Так, если источником сообщений является книга, на каждой странице которой повторяются одни и те же, уже известные, истины, то читатель получит мало информации; такая книга будет обладать низкой энтропией. Напротив, когда каждая глава, каждый параграф содержит что-то новое, книга может дать много информации читателю и, следовательно, имеет большую энтропию.