Временные характеристики цепей

Ранее мы рассматривали частотные характеристики, а временные характеристики описывают поведение цепи во времени при заданном входном воздействии. Таких характеристик всего две: переходная и импульсная.

Переходная характеристика

Переходная характеристика - h(t) - есть отношение реакции цепи на входное ступенчатое воздействие к величине этого воздействия при условии, что до него в цепи не было ни токов, ни напряжений.

Ступенчатое воздействие имеет график:

1(t) – единичное ступенчатое воздействие.

Иногда используют ступенчатую функцию, начинающуюся не в момент «0»:

Для расчёта переходной характеристики к заданной цепи подключают постоянный ЭДС (если входное воздействие – напряжение) или постоянный источник тока (если входное воздействие – ток) и рассчитывают заданный в качестве реакции переходный ток или напряжение. После этого делят полученный результат на величину источника.

Пример: найти h(t) для u_c при входном воздействии в виде напряжения.

1) ,

2) ,

3) , ,

,

,

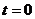Пример: ту же задачу решить при входном воздействии в виде тока

1) ,

2) ,

3) , ,

,

,

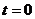Импульсная характеристика

Импульсная характеристика - g(t) – есть отношение реакции цепи на входное воздействие в виде дельта - функции к площади этого воздействия при условии, что до подключения воздействия в схеме не было ни токов, ни напряжений.

δ(t) – дельта-функция, дельта-импульс, единичный импульс, импульс Дирака, функция Дирака. Это есть функция:

Рассчитывать классическим методом g(t) крайне неудобно, но так как δ(t) формально является производной , то найти её можно из соотношения g(t)=h(0)δ(t) + dh(t)/dt.

Для экспериментального определения этих характеристик приходится действовать приближённо, то есть создать точное требуемое воздействие невозможно.

На вход падают последовательность импульсов, похожих на прямоугольные:

t_ф – длительность переднего фронта (время нарастания входного сигнала);

t_и – длительность импульса;

К этим импульсам предъявляют определённые требования:

а) для переходной характеристики:

- t_паузы должно быть таким большим, чтобы к моменту прихода следующего импульса переходный процесс от окончания предыдущего импульса практически заканчивался;

- t_и должно быть таким большим, чтобы переходный процесс, вызванный возникновением импульса, тоже практически успевал заканчиваться;

- t_ф должно быть как можно меньше (так, чтобы за t_ср состояние цепи практически не менялось);

- X_m должна быть с одной стороны такой большой, чтобы с помощью имеющейся аппаратуры можно было бы зарегистрировать реакцию цепи, а с другой: такой маленькой, чтобы исследуемая цепь сохраняла свои свойства. Если всё это так, регистрируют график реакции цепи и изменяют масштаб по оси ординат в X_m раз (X_m =5В, ординаты поделить на 5).

б) для импульсной характеристики:

t_паузы – требования такие же и к X_m – такие же, к t_ф требований нет (потому что даже сама длительность импульса t_ф должна быть такой малой, чтобы состояние цепи практически не менялось. Если всё это так, регистрируют реакцию и изменяют масштаб по оси ординат на площадь входного импульса .

Итоги по классическому методу.

Основным достоинством является физическая ясность всех используемых величин, что позволяет проверять ход решения с точки зрения физического смысла. В простых цепях удаётся очень легко получить ответ.

Недостатки: по мере возрастания сложности задачи быстро нарастает трудоёмкость решения, особенно на этапе расчёта начальных условий. Не все задачи удобно решать классическим методом (практически никто не ищет g(t), и у всех возникают проблемы при расчёте задач с особыми контурами и особыми сечениями).

До коммутации , .

Следовательно, по законам коммутации u_c1(0) = 0 и u_c2(0) = 0, но из схемы видно, что сразу после замыкания ключа: E= u_c1(0)+u_c2(0).

В таких задачах приходится применять особую процедуру поиска начальных условий.

Эти недостатки удаётся преодолеть в операторном методе.