Способы получения характеристического уравнения
Существуют различные способы получения характеристического уравнения.
Если цепь описывается всего одним уравнением, то его алгебраизируют: d/dt заменяют на p, 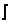 dt заменяют на 1/p, правую часть обращают в ноль и получают характеристическое уравнение.
dt заменяют на 1/p, правую часть обращают в ноль и получают характеристическое уравнение.
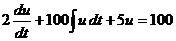
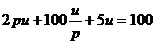
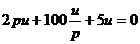
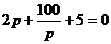
Если режим в цепи описывается системой из нескольких уравнений, то методом подстановки их сводят к одному и поступают точно также как описано выше (обычно так не делает).
Универсальный способ
Систему уравнений по законам Кирхгофа для цепи после коммутации алгебраизируют и составляют определитель системы, и приравняв его к нулю, получают характеристическое уравнение.
Воспользуемся этим способом.
Пусть схема после коммутации имеет вид:
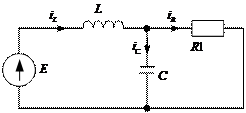
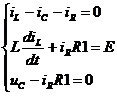 , ,
, ,
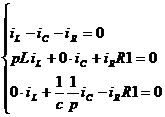
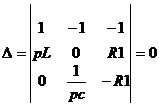
Если в схеме нет управляемых источников и взаимных индуктивностей, то проще всего поступить так: в схеме после коммутации все источники заменить их внутренним сопротивлением, вместо индуктивности L написать pL, вместо емкости C написать 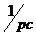 .
.
а) Если в полученной схеме нет ветви без сопротивления, томожно разомкнуть любую ветвь полученной пассивной схемы и относительно точек разрыва записать выражение для нахождения 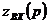 .
.
б) Если в полученной схеме есть ветви без сопротивления, то размыкать надо именно ту ветвь, в которой ищется переходный ток или напряжение и относительно точек разрыва записывают 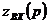 .
.
Характеристическое уравнение имеет вид: 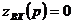 .
.
Для рассмотренного выше примера получим:
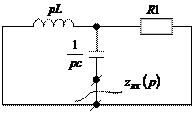
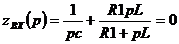
Выражение для свободной составляющей содержит столько слагаемых, сколько есть корней, а слагаемые имеют такой вид:
а) каждому простому вещественному корню 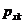 соответствует слагаемое
соответствует слагаемое 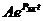 .
.
Если два корня, то процесс апериодический.
б) двум комплексно-сопряженным корням: 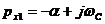 и
и 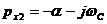 соответствует A1ePx1 t +A2ePx2 t, где A1, A2 – получаются комплексными числами, причем комплексно-сопряженными числами. Поэтому с помощью формулы Эйлера этот результат можно записать в другом виде (где не будет j):
соответствует A1ePx1 t +A2ePx2 t, где A1, A2 – получаются комплексными числами, причем комплексно-сопряженными числами. Поэтому с помощью формулы Эйлера этот результат можно записать в другом виде (где не будет j): 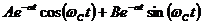 .
.
По этому выражению не очень удобно строить графики. Используя формулы тригонометрии его можно преобразовать (либо в sin, либо в cos): Ce- 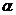 t sin(
t sin( 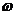 ct+
ct+ 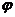 1)=De-
1)=De- 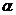 t cos(
t cos( 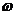 c t+
c t+ 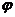 2) – затухающий во времени гармонический процесс – колебательный процесс.
2) – затухающий во времени гармонический процесс – колебательный процесс.
в) среди корней есть m одинаковы[ (если таких корней два, то переходный процесс называется критическим).
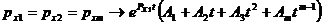
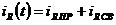 ;
;
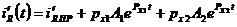
Пример: Дано: E=40В, R1 =R2=400 Ом, L=5Гн, C=5 мкФ. Найти 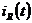 .
.
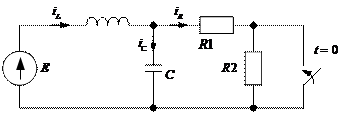
1) В схеме до коммутации стоит постоянный источник, следовательно, ток в установившемся режиме постоянный.
t<0

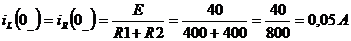 ,
, 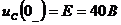 .
.
Если источник ЭДС синусоидальный, то эту часть задачи решают символическим методом.
2) Рассчитывают новый установившийся режим, находят принужденную составляющую.
t 
Видно, что после коммутации в схеме есть только постоянный источник ЭДС и поэтому в принужденном режиме – постоянный ток.

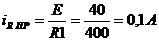 .
.
3) получают характеристическое уравнение
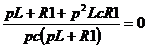
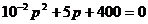
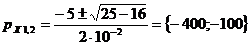 .
.
4) записывают решение
5) определяют начальные условия
Для схемы после коммутации записывают систему уравнений по законам Кирхгофа. Число этих уравнений больше, чем число неизвестных, однако при t=0, известны все iL(0) и uC(0), поэтому при добавлении этих независимых условий из полученной при t=0 системы можно найти все остальные зависимые начальные условия, например, методом подстановки.
При решении надо выразить значения токов и напряжений в момент t=0, их производные по времени в момент t=0 через параметры элементов схемы и независимые начальные условия.
Например, для нашей задачи:
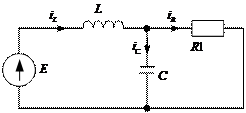
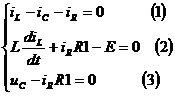
В нашей задаче для расчета 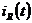 надо найти 2 начальных условия, т.к. имеем 2 корня характеристического уравнения и 2 произвольные постоянные, поэтому надо знать
надо найти 2 начальных условия, т.к. имеем 2 корня характеристического уравнения и 2 произвольные постоянные, поэтому надо знать 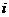 R(0) и
R(0) и 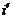 R(0).
R(0).
Из (1): 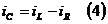 ,
,
Из (3): 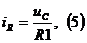
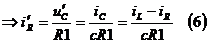
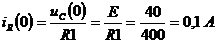 ,
,
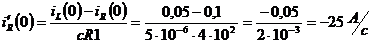 .
.
6) расчет произвольных постоянных
В нашем случае:
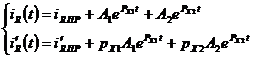

При 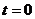 :
:
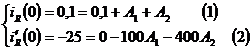
Тогда из (1) 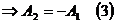
Из (3) 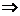 (2)
(2) 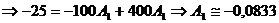
Ответ: 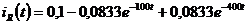 , А.
, А.
