Способы представления и описания

Самым подробным описанием является задание мгновенных значений i(t) и u(t).

Чаще всего это делают в виде графика. Например:

Для сравнительно простых функций можно применить аналитическое описание, разбив период функции на отрезки и на каждом отрезке заменив функцию некоторым аппроксимированным выражением. Например, для первой кривой

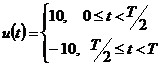
для второй

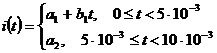
Из графика видно, что а₂ = 0,5, а для нахождения a₁ и b₁ надо составить два уравнения для каких–то двух моментов времени. Например:

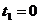
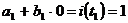
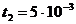
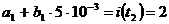
Решая систему получаем а₁ = 1, а b₁ = 200 А/с.

Очень часто применяют разложение периодических несинусоидальных функций в функциональные ряды. Например, в ряд Фурье. Любая периодическая функция с конечным числом разрывов первого рода и с конечным числом max и min на периоде может быть представлена тригонометрическим рядом Фурье (условия Дирихле):

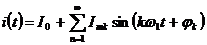, (1)

иногда пишут 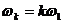. Каждое слагаемое этого выражения называют гармоникой с номером k (синусоидой с номером k). Иногда отдельно называют I₀ – постоянной составляющей или среднем значением функции за период. k – номер гармоники (показывает во сколько раз частота данной гармоники больше частоты первой гармоники 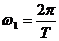). Период k - гармоники в k раз меньше периода всего сигнала. 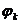– начальная фаза, 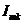– амплитуда k гармоники.

Выражение (1) можно переписать:

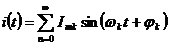(2)

Используя формулы Эйлера для мнимого аргумента ряд (1) или (2) можно переписать в комплексной форме, если ввести отрицательные частоты

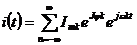(3)

Число слагаемых ряда бесконечно велико, но на практике всегда ограничивается конечным числом слагаемых. Как узнать, сколько надо взять гармоник? Никто не знает, но при решении конкретной задачи выбирают некоторые критерии точности решения, после этого берут первую или несколько первых гармоник и решают задачу до конца. Затем добавляют ещё одну гармонику и повторяют всё решение. Если разница первого и второго решения удовлетворяет выбранному критерию, считается, что второй вариант учитывает необходимое число гармоник. Если же нет, добавляют следующую гармонику, получают новое решение и сравнивают его с предыдущим и т. д.

Ряд (1) даёт спектр сигнала – графическое изображение зависимости амплитуд и начальных фаз от номера гармоники, например, для сигнала рис.1:

Чётные гармоники отсутствуют, а нечётные непрерывно убывают. Спектр такого вида называют дискретным или линейчатым, потому что разность частот соседних гармоник отлична от нуля.

Для простых функций в справочниках приведены таблицы разложения в ряд Фурье. Для более сложных функций коэффициенты ряда приходится вычислять.

Пусть есть функция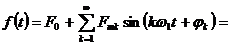

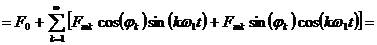
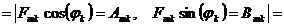
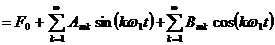
Коэффициенты этого ряда находят из выражений:

, ,

, ,

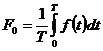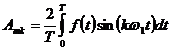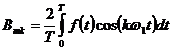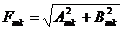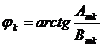
В некоторых задачах не нужно иметь такое подробное описание несинусоидальной кривой и тогда применяют более простые описания с помощью специальных величин.

Например: