Способы «замены» индуктивных связей

1) В любой цепи можно «устранить» индуктивные связи, введя управляемые источники определённой величины.

Например: в некоторой схеме есть две ветви 12 и 34, в которых есть катушки с индуктивной связью между собой:

Запишем напряжение для каждой ветви: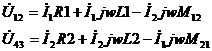

и по полученным выражениям подберём схему замещения:

Теперь можно пользоваться любыми методами записи уравнений, но возникают все оговорки, связанные с наличием управляемых источников.

2) Замена индуктивных связей с помощью дополнительных индуктивностей (развязка индуктивных связей). Этот приём используют тогда, когда индуктивно связанные катушки стоят в ветвях, присоединённых к одному и тому же узлу.

Катушки присоединены к общему узлу одноимёнными зажимами. Запишем уравнения для и , искусственно преобразуем их, а после этого придумаем схему, которая соответствует придуманным уравнениям.

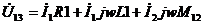
К правой части данного уравнения добавим и отнимем одну и ту же величину :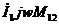

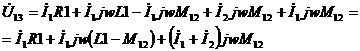
Аналогичным образом поступим для :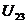

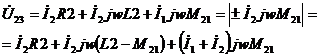
Полученным уравнениям соответствует следующая схема.

Рассмотрим случай, когда катушки присоединены к общему узлу разноимёнными зажимами:

Произведя точно такие же манипуляции, получим следующую схему замещения:

Пример: найти входное сопротивление

.

Трансформатор

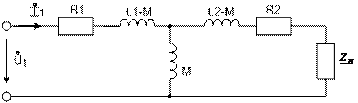
Название трансформатор означает преобразователь энергии и представляет собой систему индуктивно связанных катушек, не имеющих электрической связи. Для увеличения коэффициента связи обычно эти катушки размещают на ферромагнитном сердечнике, поэтому в общем случае трансформатор – устройство нелинейное. Но если индукция в сердечнике мала, то в первом приближении нелинейностью можно пренебречь. И тогда получают линейный трансформатор, который будет рассмотрен далее. В простейшем случае трансформатор содержит две катушки (см. рис.):

Рис. 1

где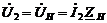

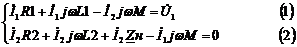
Из уравнения (2) получим

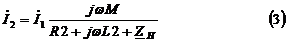
Подставим 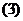в уравнение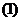

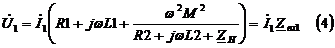
Видно, что входное сопротивление со стороны первичных зажимов зависит от параметров элементов первичной цепи, от частоты и коэффициента взаимной индукции и от параметров элементов вторичной цепи.

Введем обозначение:

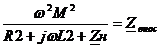
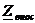- это есть некоторое сопротивление, отражающее эффект влияния вторичной цепи на режим первичной.

По выражению (4) строим соответствующую схему замещения.

Режим цепи рис. 1 не изменится, если соединить проводом нижние концы катушек (на практике этого делать не надо). Тогда можно воспользоваться развязкой индуктивных связей и получить другую схему замещения трансформатора:

Судя по выражению (4) 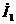зависит от всех параметров схемы и от частоты. Следовательно, 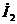тоже будет зависеть от всех величин, а также от 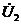. Это крайне не удобно, так как трансформатор предназначен для вполне конкретного заранее заданного изменения величин токов и напряжений. Желательно характеризовать трансформатор одним числом: коэффициентом трансформации 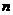, равным .

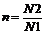Вводится понятие идеального трансформатора, который обладает указанными выше свойствами и к которому стремятся подогнать при проектировании реальный трансформатор. Анализ показывает, что трансформатор отвечает идеальным требованиям, если:

1) активное сопротивление катушек равно 0;

2) коэффициент связи равен 1, следовательно ;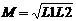

3) на рабочей частоте >> .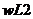

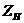Схема идеального трансформатора представлена на рис.2

Рис. 2

Из условия 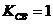получается, что

, ,

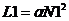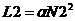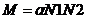
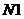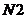, – число витков катушек, а 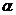– некоторый коэффициент пропорциональности, определяемый конструкцией данного трансформатора.

Запишем систему Кирхгофа для идеального трансформатора.

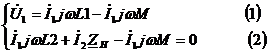
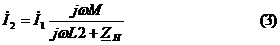
Подставим (3) в (1):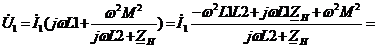

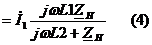
Выразим 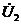через :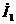

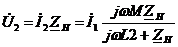
Из (4) выражаем 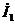и подставляем в выражение для :

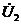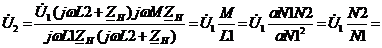
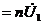(5)

где 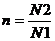- коэффициент трансформации.

Учтем в (3) условие 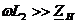, тогда величиной 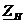в знаменатели можно пренебречь, и получим:

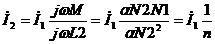(6)

Из (4) следует, что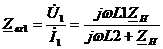

Воспользуемся условием 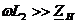, тогда величиной 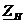в знаменателе можно пренебречь:

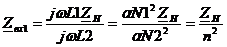(7)

Найдём комплекс полной мощности, потребляемой на входе трансформатора с учетом (5) и (6).

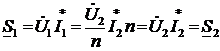
Т.е. в идеальном трансформаторе комплекс полной мощности, поступающий на вход трансформатора без потерь попадает в нагрузку (тоже самое относится к активной и реактивной мощностям).

Рассмотренные выше свойства идеального трансформатора очень близки к свойствам реального трансформатора (отличие не более нескольких %).

Из этих свойств вытекают следующие основные применения трансформатора:

1. Преобразование величины напряжения и тока в заданное число раз практически без потерь мощности;

2. Гальваническая развязка двух цепей;

3. Для согласования генератора с нагрузкой в целях получения от генератора максимальной активной мощности.

Пусть есть генератор с чисто активными внутренними сопротивлениями 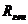и нагрузкой .

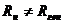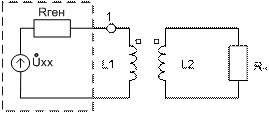
Рис. 3

В этом случае между генератором и нагрузкой включают трансформатор с числом витков .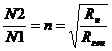

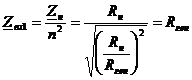
Следовательно, генератор согласован с входным сопротивлением трансформатора. На вход трансформатора поступает максимально возможная активная мощность, которая потом передаётся в нагрузку без потерь.

Трехфазные цепи