Основные показатели долговечности

Струков Валерий Григорьевич

НАДЕЖНОСТЬ МЕХАНИЧЕСКОГО

ОБОРУДОВАНИЯ

Учебное пособие

Редактор

Корректор

Изд. лиц. Подписано в печать

Формат 60х84/16 Объем 6 п. л. Тираж экз.

Заказ Цена

УДК 621.86

ББК 34.41

С 87

Автор:В.Г.СТРУКОВ

Рецензенты: В.В. Абрамов, д.т.н., проф., (МИКХиС, г. Москва); Я.Л. Певзнер, (ген директор ОАО «БЕЛАЦИ», г. Белгород)

Струков В.Г. Надежность механического оборудования: С 87Учеб. пособие. – 2-е изд., перераб. и доп. - М: Изд-во АСВ, 2005. – 144 с.: 38 ил.

ISBN 5-93093-054-6

Приведены основные понятия и термины теории надежности. Показано применение теории вероятностей для изучения теоретических вопросов и математической статистики при обработке эмпирических результатов. Рассмотрено определение показателей надежности машин и использование распределений случайных величин. При определении надежности механического оборудования в процессе эксплуатации рассматриваются потоки отказов и восстановлений машин.

Предназначено для студентов специальности 171600 «Механическое оборудование и технологические комплексы предприятий строительных материалов, изделий и конструкций». Может быть полезно для аспирантов и инженеров-механиков.

ISBN 5-93093-054-6

УДК 621.86

ББК 34.41

© Издательство БегГТАСМ, 1987

© Издательство БелГТУ им. В. Г. Шухова, 2005, с изменениями

© Издательство АСВ, 2005, с изменениями

ВВЕДЕНИЕ

Цель курса "Надежность механического оборудования" - в обеспечении комплексной подготовки студентов-механиков.

Курс является дисциплиной, формирующей научные основы создания и эксплуатации механического оборудования предприятий строительных материалов, изделий и конструкций. На базе общих методов теории надежности рассматриваются вопросы обеспечения надежности механического оборудования в процессе его проектирования, производства и эксплуатации, образующих единый процесс.

Обеспечение планируемого уровня показателей надежности механического оборудования при эксплуатации требует рассмотрения особенностей организации технического обслуживания, диагностирования и ремонта механического оборудования и комплекса работ по поддержанию машин на требуемое время в работоспособном состоянии.

Сейчас большое внимание уделяется развитию механического оборудования. На это направлен ряд постановлений правительства о развитии цементной промышленности (сухой способ), кирпичного производства (силикатный и керамический кирпич), производство гипса и извести, стекла и ситаллов, пластмассы и полимеров. Важнейшим показателем качества является надежность машин, от которой в значительной степени зависит эффективность использования механического оборудования.

Теория надежности как самостоятельное научное направление сформировалось сравнительно недавно. Первые работы в области надежности деталей машин и элементов металлоконструкций принадлежат советским инженерам и ученым - Н.Ф. Хоциалову (1929), Н.С. Стрелецкому (1935). Общие вопросы надежности машин и их элементов рассмотрены в работах А.С. Пронникова и Д.Н. Решетова.

Человек стремится все сделать как можно надежнее в меру своих сил и возможностей. Создавать совершенно безотказную и предельно долговечную машину невозможно, так как с течением времени на нее воздействуют различные факторы, изменяются свойства деталей и, следовательно, происходит отклонение показателей надежности. Экономически создавать такую машину нецелесообразно, так как со временем изменяются технологии, сами машины, мода и эстетика.

Сначала надежность как наука возникла в авиационной и космической технике, позже - в радиотехнике, телемеханике, средствах связи. Она стала "проблемой номер один" и выделилась в самостоятельную дисциплину, главная задача которой дать оценку надежности объекта.

Наука о надежности техники изучает закономерности изменения показателей работоспособности объектов с течением времени, а также физическую природу отказов и на этом основании разрабатывает методы, обеспечивающие с наименьшей затратой времени и средств необходимую долговечность и безотказность работы.

Надежность объекта - один из основных показателей его качества.

Проблема надежности техники - комплексная проблема, состоящая из связи многих этапов, среди которых выделяются следующие:

1. Утверждение идеи, исследование, проектирование и расчет объекта определенной надежности. Надежность на этой стадии зависит от качества проведенных исследований и конструкторских расчетов.

Это самый ответственный этап, при котором ошибка в один рубль при выборе принятого решения влечет за собой убытки в тысячи рублей на этапе эксплуатации.

2. Производство объекта. Надежность его на этом этапе в первую очередь зависит от качества материала деталей и точности их изготовления, от качества сборки и обкатки, от других составляющих технологического процесса.

Ошибка в осуществлении технологии в один рубль на этом этапе обернется в сотни рублей на этапе эксплуатации. Следует заметить, что на большинстве предприятий не проводятся полная обкатка и испытание объектов продукции. Необходимо повсеместно внедрять ускоренные испытания как новой, так и отремонтированной техники.

3. Эксплуатация объекта. На этом этапе реализуется и поддерживается надежность, заложенная при расчете и обеспеченная при изготовлении. Обычно рассматривают цепочку "человек - машина - среда", которая описывает процессы эксплуатации, обслуживания и ремонта. Необходимо добавить и социальный фактор (условия труда и быта, заработную плату, участие обслуживающего персонала в жизни коллектива и др.), который в ряде случаев может быть определяющим.

Отсюда следует: рассчитывать, изготавливать и эксплуатировать долговечное оборудование - основное содержание науки о надежности.

ПОНЯТИЯ И ТЕРМИНЫ ТЕОРИИ НАДЕЖНОСТИ. ГОСУДАРСТВЕННЫЙ СТАНДАРТ НА ПОКАЗАТЕЛИ НАДЕЖНОСТИ

Надежность машин отражает изменение их свойств во времени в процессе эксплуатации.

ГОСТ 27002-83 "Надежность в технике. Термины" содержит 21 показатель надежности техники и 86 терминов, разделенных на следующие группы:

1) общие понятия;

2) виды отказов;

3) показатели надежности;

4) термины, относящиеся к резервированию.

Термины надежности машин

Рассмотрим некоторые термины ГОСТ 27002-83 и общие понятия, приводимые в специальной литературе по надежности.

Технические объекты могут находиться в следующих состояниях:

1) исправном и неисправном;

2) работоспособном и неработоспособном;

3) предельном.

Исправность (исправное состояние) - состояние объекта, при котором он соответствует всем требованиям, установленным нормативно-технической и конструкторской документацией.

Неисправное состояние - состояние объекта не соответствует хотя бы одному из требований нормативно-технической и конструкторской документации, например: снижение производительности, экономичности, потеря точности, вмятины на кожухе, отклонения в толщине слоя окраски и т.д. Неисправности - это нефункциональные дефекты.

Работоспособное состояние - это состояние объекта, когда он способен выполнять заданные функции, сохраняя значения заданных параметров в пределах, установленных нормативно-технической и конструкторской документацией.

Понятие "исправность" шире, чем понятие "работоспособ-ность". Исправный объект всегда работоспособен. Работоспособный объект может быть неисправным, но неисправность при этом не влияет на функционирование объекта (например, шестерни изношены, но эксплуатационные показатели не вышли за пределы технических требований).

Неработоспособность - состояние объекта, когда значение хотя бы одного заданного параметра, характеризующего способность выполнять заданные функции, не соответствует требованиям, установленным нормативно-технической или конструкторской документацией. К неработоспособности относятся функциональные дефекты.

Предельное состояние - состояние объекта, когда его дальнейшая эксплуатация должна быть прекращена из-за неустранимого ухода заданных параметров за установленные пределы, или неустранимого снижения эффективности эксплуатации ниже допустимой, или необходимости проведения капитального ремонта. Критерии предельного состояния устанавливаются нормативно-технической и конструкторской документацией.

Причины прекращения эксплуатации, невозможность обеспечения безопасности или эффективности эксплуатации объекта и минимума необходимого уровня безопасности, экономическая нецелесообразность.

Событие, заключающееся в нарушении исправного состояния, называется повреждением.

Событие, заключающееся в нарушении работоспособности, называется отказом. Процесс возникновения отказов показан на рис. 1:

Энергия, дей- Изменение Повреждение Изменение

ствующая на свойств или материала и выходных

машину состояния деталей параметров

материала машин машин

О т к а з

Рис. 1. Процесс возникновения отказов

Внезапный отказ характеризуется скачкообразным изменением одного или нескольких параметров объекта. Внезапному отказу не предшествует направленное изменение какого-нибудь из наблюдаемых эксплуатационных параметров.

Постепенный отказ имеет место, когда один или несколько параметров объекта изменяются постепенно.

Независимый отказ не обусловлен отказом другого объекта, зависимый - обусловлен отказом другого объекта.

При отказе, в зависимости от ситуации, работоспособность объекта может как восстанавливаться, так и не восстанавливаться. Поэтому при анализе надежности различают восстанавливаемые и невосстанавливаемые объекты.

Восстанавливаемый объект - объект, для которого в данной ситуации предусмотрено научно-технической и конструкторской документацией восстановление работоспособного состояния. В противном случае объект называется невосстанавливаемым.

Ремонт - комплекс операций по восстановлению исправности или работоспособности, а также ресурсов объектов и их составных частей.

Ремонтируемые объекты - объекты, для которых проведение ремонтов предусмотрено нормативно-технической и конструкторской документацией, в противном случае - неремонтируемые (например: поршневые кольца, фрикционные накладки тормозов и сцепления, прокладки, уплотнительные кольца).

Показатели надежности машин

Надежность - сложное свойство, которое, в зависимости от назначения объекта и условий его применения, характеризуется безотказностью, долговечностью, ремонтопригодностью и сохраняемостью.

Безотказность - свойство, показывающее возможность объекта непрерывно сохранять работоспособное состояние в течение заданного времени или заданной наработки. Особенностью безотказности является непрерывное сохранение работоспособности в течение заданного времени. Это свойство особенно важно для объектов, отказ в работе которых связан или с опасностью для жизни людей, или с большими экономическими потерями.

Долговечность - свойство объекта сохранять работоспособное состояние до наступления предельного состояния при установленной системе технического обслуживания и ремонта.

Для невосстанавливаемых объектов понятия долговечности и безотказности практически совпадают.

Ремонтопригодность - свойство объекта, заключающееся в приспособленности к предупреждению и обнаружению причин возникновения отказов, повреждений, а также поддержанию и восстановлению работоспособности проведением технического обслуживания и ремонтов. Количество ремонтопригодности определяется затратами времени, труда и средств.

Ремонтопригодность определяет доступность, контролепригодность, агрегатирование, легкосъемность, взаимозаменяемость, унификацию, количество смазываемых точек и т.д.

Сохраняемость - свойство объекта сохранять значения показателей безотказности, долговечности и ремонтопригодности в течение хранения и после него и (или) транспортирования. Наиболее эффективные методы повышения сохраняемости - консервация, применение специальных защитных покрытий и пропитывающих составов, профилактическое обслуживание хранящихся объектов, повышение транспортабельности объектов, защита от старения полимеров.

Наработка

Наработка - продолжительность или объем работы объекта. Наработка измеряется в единицах времени, массы, длины, площади, объемах, циклах и т.д., например: шина - километры пробега, экскаватор - метры кубические грунта, реле - циклы включения, телевизор - часы работы.

Наработка может быть суточной, месячной, до первого отказа, между отказами, до предельного состояния и т.д. При различных режимах эксплуатации каждый уровень учитывается отдельно.

Наработку не следует смешивать с календарной продолжительностью эксплуатации. Например, наработка грузоподъемного механизма (лифта) в течение года может составлять 1000 часов, хотя в году 8760 часов.

Наработка - обобщающее понятие для продолжительности или объема работы объекта.

Теоремы теории вероятностей

1. Формула сложения вероятностей. Если при испытаниях может произойти только одно из рассматриваемых событий A₁, A₂,...,A_n, а вместе они появиться не могут, то эти события несовместные. Рассматриваемое сложное событие А называют суммой исходных событий:

A=A₁+A₂+...+A_n= 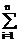A_i.

Если вероятности событий подчиняются таким же соотношениям, как и соответствующие им частости, то получим теорему (формулу) сложения вероятностей:

P(A)=P(A₁+A₂+...+A_n)=P(A₁)+P(A₂)+...+P(A_n)= 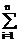P(A_i).

B общем случае для полной группы несовместных событий

P(A_n)= 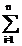P(A_i)=1. (2)

Полная группа событий - события, когда в результате испытаний обязательно наступит хотя бы одно из них. Например, при длительных испытаниях механического оборудования обязательно появится отказ.

Для двух несовместных событий A и 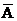, образовавших полную группу,

P(A)=1-P( 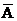). (3)

Например, в надежности чаще рассматриваются два несовместных противоположных события - состояние работоспособности и отказ. Они составляют полную группу.

Для двух совместных событий A₁ и A₂, образовавших полную группу,

P(A₁+A₂)=P(A₁)+P(A₂)-P(A₁A₂). (4)

2. Формула умножения вероятностей. Если события независимы, то появление одного из них не изменяет вероятности появления другого:

P(AB)=P(A)P(B). (5)

Для двух зависимых событий

P(A)=P(B)P(AB)=P(A)². (6)

Сложное событие A, заключающееся в одновременном осуществлении нескольких событий, называется произведением исходных событий A_i:

A=A₁A₂...A_n= .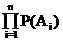

Вероятность независимых событий по теореме умножения вероятностей

P(A)=P(A₁,A₂,...,A_n)=P(A₁)P(A₂)...P(A_n)= 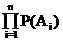. (7)

Если

P(A₁)P(A₂)=...=P(A)=P,

то

= .

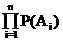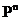Случайной величины

Интегральная функция распределения вероятностей случайной величины - одна из форм закона распределения.

Наибольшее распространение в теории надежности имеют события вида Х<х, то есть случайная величина Х принимает значение, меньшее некоторого действительного числа х. Рассматривая действительное число х как независимую переменную, получают интегральную функцию распределения случайной величины Х.

Интегральной функцией распределения случайной величины Х называется функция F(x), определяющая вероятность события Х<х для каждого значения аргумента х, то есть

F(x)=P(Х<х).

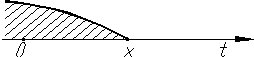Геометрически это значит, что F(x) - вероятность того, что случайная величина х примет значение, изображенное на числовой оси точкой, расположенной левее точки х (рис. 7).

Рис. 7. Геометрический смысл интегральной функции распределения

Интегральная функция F(x), как всякая вероятность, - величина безразмерная. Она полностью характеризует случайную величину (с вероятностной точки зрения) и является самой универсальной характеристикой случайной величины, т.к. существует и для дискретных, и для непрерывных случайных величин. Для краткости используют следующие термины:

1) интегральная функция распределения;

2) интегральная функция;

3) функция распределения.

Вероятность отказа объекта

Вероятность отказа объекта - это функция F(t), определяющая для каждого значения времени t вероятность события T<t, то есть время Т работы объекта до отказа примет значение, меньшее t:

F(t)=P(T<t).

Вероятность отказа объекта - интегральная функция распределения вероятностей времени работы объекта до отказа, определяющая вероятность возникновения отказа объекта в интервале времени t.

По статистической информации F*(t) определяется как отношение числа объектов, отказавших за время t, к числу объектов в начале испытания:

F*(t)= 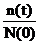= =1- 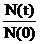=1-P*(t),

где n(t) - число объектов, отказавших за время t; N(t) - число объектов, работоспособных в момент времени t; N(0) - число объектов в начале испытаний, N(0)=N(t)+n(t); P*(t) - вероятность безотказной работы.

Частота появления событий

Частота появления событий - это вероятность их появления в единицу времени.

Непрерывные случайные величины в теории надежности связаны с событиями, в результате которых случайная величина принимает то или иное случайное значение.

Дифференциальная функция (плотность распределения) может быть представлена как частота появления событий (например, частота отказов объектов, частота восстановления объектов).

Частота отказов по статистической информации определяется как отношение числа объектов, отказавших в единицу времени, к числу объектов в начале испытания:

f*(t)= = ,

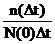где Dt - интервал времени от t до t+Dt; n(Dt) - число объектов, отказавших в интервале времени Dt; n(t) - число объектов, отказавших за время t; N(0) - число объектов в начале испытания, N(0)=N(t)+n(t).

Не появлялось

Вероятность появления события на интервале, следующем за интервалом, на котором событие не появлялось, является условной вероятностью.

Для определения найдем сначала условную вероятность P_t(Dt) непоявления события на интервале Dt при условии непоявления события на предыдущем интервале t (рис. 14).

По теореме умножения вероятностей зависимых событий можно записать

P(t+Dt)=P(t)P_t(Dt), (17)

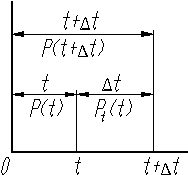где P(t) - безусловная вероятность непоявления события на интервале t; P(t+ Dt) - безусловная вероятность непоявления события на интервале t+Dt, то есть вероятность одновременного непоявления событий и на интервале t, и на интервале Dt. Условная вероятность непоявления события (отказа, восстановления работоспособности) на интервале Dt

при условии непоявления события Рис.14. Интервалы времени

на предыдущем интервале t

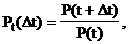(18)

то есть равна отношению вероятностей непоявления события в конце и в начале рассматриваемого интервала времени Dt.

Условная вероятность появления события (отказа, восстановления работоспособности) на интервале Dt при условии непоявления события на предыдущем интервале t

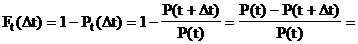
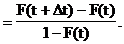(19)

Интенсивность событий

Интенсивность событий (отказов, восстановления работоспособности) - функция l(t), определяющая вероятность появления события в единицу времени в момент t при условии, что событие не появилось до момента t.

Интенсивностью событий является плотность вероятности появления события в момент t при условии, что событие не появлялось до момента t.

Условная вероятность появления события в единицу времени на интервале Dt из формулы (19) равна

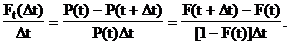
Интенсивность событий получается в результате перехода в уравнении к пределу при Dt®0

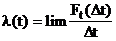
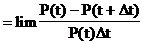
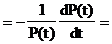
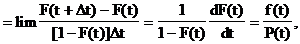
то есть

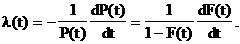(20)

Интенсивность событий по статистической информации определяется как отношение числа объектов, отказавших в единицу времени, к числу объектов, работоспособных в данный момент времени:

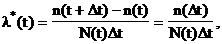
где Dt - интервал времени от t до t+Dt; n(Dt) - число объектов, отказавших в интервале времени Dt; N(t) - число объектов, работоспособных в момент времени t.

Для определения вероятности появления событий через их интенсивность производим интегрирование. Из уравнения (20) имеем

-l(t)dt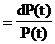

интегрируем его:

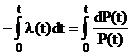=lnP(t)-lnP(0)=lnP(t).

Откуда

P(t)= 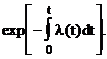(21)

Математическое ожидание

Математическое ожидание (среднее значение) непрерывной случайной величины Х, возможные значения которой принадлежат интервалу (a,b), представляет собой определенный интеграл

X_ср.=<X>= 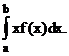(22)

Математическое ожидание можно выразить через дополнение интегральной функции. Для этого в формулу (22) подставляем формулу (13) для определения дополнения интегральной функции и проинтегрируем по частям:

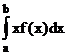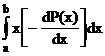<X>= = =- =-xP(x)+ =

=-b P(b)+a P(a)+ =a+ .

Так как P(b)=0, P(a)=1, то

X_ср.=<X>= 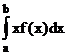=a+ . (23)

Для неотрицательных случайных величин, возможные значе-

Т а б л и ц а 1

Ряд распределения случайной величины

Значения случайной

величины Х₁ Х₂ ... ... Х_n

Вероятность

Р(Х=Х_i)=Р Р₁ Р₂ ... ... Р_n

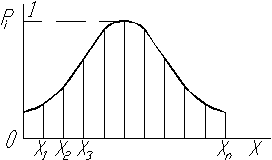При графическом представлении по оси абсцисс откладываются значения случайной величины, по оси ординат - вероятности Р_i , соответствующие этим значениям.

Рис. 2. Многоугольник распределения случайной величины

Ряд распределения удобен, когда закон распределения дискретной случайной величины имеет конечное число значений. В случае непрерывной случайной величины, имеющей бесчисленное множество значений, такая форма закона неприемлема. В этом случае используют не вероятность события Р_i(x=x_i), а вероятность P(X<x_i). Следовательно, случайная величина X примет значение, меньшее какого-либо наперед заданного (-¥<x<+¥).

Наиболее универсальной характеристикой как дискретных (прерывных), так и непрерывных случайных величин является функция или интегральный закон распределения случайной величины.

Пусть X - случайная величина и x - некоторое действительное число, тогда вероятность того, что X<x

F(x)=P(X<x),

где F(x) - функция распределения.

Эту функцию можно представить в виде графика , где по оси абсцисс отложены значения х, а по оси ординат - значения F(х). График функции непрерывной случайной величины - плавная кривая при любом значении (рис. 3).

Если Х - дискретная величина, то на основании теоремы сложения вероятностей несовместных событий

F(x)= .

В этом случае график имеет ступенчатый вид (рис. 4). С увеличением числа значений x число ступеней будет увеличиваться, а их величина - уменьшаться.

Рис. 3. График функции непре- Рис. 4. График функции диск-

рывной случайной величины ретной случайной величины

Из графиков видно, что функция распределения изменяется в пределах

0<F(x)<1.

ОБЪЕКТА (ЕПНО)

Медиана случайной величины

Медиана случайной величины является ее гамма-процентным значением при g=50%. Для медианы Me(t) одинаково вероятно, окажется ли случайная величина Т больше или меньше ее, то есть

P[T>Me(T)]=P[T<Me(T)].

Геометрически медиана является абсциссой точки пересечения интегральной функции распределения и ее дополнения (см. рис. 17). Медиану можно истолковать как абсциссу точки, в которой ордината дифференциальной функции делит пополам площадь, ограниченную кривой распределения (см. рис. 18).

В теории надежности медиану используют как числовую характеристику ресурса, срока службы, срока сохраняемости.

БЕЗОТКАЗНОСТЬ СИСТЕМЫ

Для анализа и расчета показателей надежности объектов, которые являются системами, состоящими из нескольких элементов, применяется метод структурных схем.

Метод позволяет определить безотказность объекта по известной безотказности каждого его элемента. Он заключается в том, что объект представлен в виде структурной схемы, на которой события или соответствующие им состояния элементов изображаются в виде последовательно или параллельно соединенных звеньев, выражающих безотказность отдельных элементов системы.

Рассмотрим безотказность объекта при последовательном, параллельном и смешанном соединениях элементов.

Соединении элементов

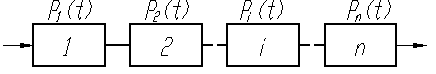Безотказность системы, изображенной на рис. 19, определяется при условии, что отказ каждого элемента является случайным не зависимым событием. Отказ любого элемента приводит к отказу всей системы.

Рис. 19. Последовательное соединение элементов

Вероятность P_c(t) безотказности системы в течение времени t при последовательном соединении элементов определяется по теореме умножения вероятностей независимых событий как произведение вероятностей безотказной работы ее элементов в течение того же времени:

P_c(t)= P₁(t) P₂(t)... P_i(t)... P_n(t)= (28)

где n - число последовательно соединенных элементов; P_i(t) - вероятность безотказной работы i-го элемента.

Вероятность безотказной работы системы можно выразить через интенсивность отказов ее элементов по формуле

P_c(t)=exp[-] exp[-]... exp[-]...

...exp[-]=exp[-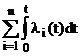]. (29)

Для равнонадежных элементов вероятности безотказной работы системы при Pi(t)=P(t) и l_i(t)=l(t)

P_c(t)= 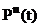= exp[ 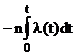]. (30)

Из формул (28)-(30) следует:

1. Вероятность безотказности системы уменьшается с увеличением числа последовательно соединенных элементов. Следовательно, при разработке объекта необходимо стремиться к возможно меньшему числу последовательно соединенных элементов.

2. Вероятность безотказности работы системы всегда меньше вероятности безотказности работы наименее надежного элемента. Следовательно, при разработке объекта необходимо выявлять наименее надежный элемент и повышать вероятность его безотказной работы.

Из формулы (29) следует, что интенсивность отказов системы в момент времени t равна сумме интенсивностей отказов составляющих ее элементов при любых распределениях вероятностей наработки на отказ элементов системы:

l_c(t)= l₁(t)+ l₂(t)+...+ l_i(t)+...+ l_n(t)=

Безотказность объектов при последовательном соединении элементов в период нормальной эксплуатации при внезапных отказах, когда явления старения и изнашивания объекта настолько слабо выражены, что ими можно пренебречь, является результатом воздействия многих случайных факторов при неизменных внешних условиях. Поэтому внезапные отказы в период нормальной эксплуатации имеют постоянную интенсивность l(t)=l=const.

Вероятность безотказной работы при постоянной интенсивности отказов имеет экспоненциальное распределение P(t) = =exp(-lt) и формулы (18), (19) принимают вид

P_c(t) 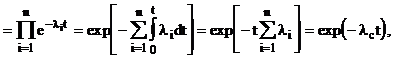(31)

где l_i - интенсивность отказов i-го элемента системы.

Из формулы (31) следует, что при экспоненциальном распределении длительности безотказной работы системы из последовательно соединенных элементов также будет экспоненциальным распределение с интенсивностью отказов l_c, равной сумме интенсивностей l_i отказов элементов:

l_c= = l₁+ l₂+...+ l_i+...+l_n. (32)

В этом случае среднее время безотказной работы системы

(33)

где T_ср.i. - среднее время безотказной работы i-го элемента.

Для однотипных элементов при l =l_i и T_ср.i. = T_ср. из формул (32) и (33) следует

l_c=nl, T_ср.i.= .

То есть интенсивность отказов системы в n раз больше интенсивности отказов одного элемента, а среднее время безотказной работы системы в n раз меньше среднего времени безотказной работы одного элемента.

Соединении элементов

Безотказность системы, изображенной на рис. 20, определяется при условии, что отказ каждого элемента является случайным независимым событием.

Отказ любого элемента при параллельном соединении не приводит к отказу всей системы. Отказ системы произойдет только если откажут все параллельно соединенные элементы.

Вероятность отказа системы F_с(t) в течение времени t при параллельном соединении элементов определяется по теореме умножения вероятностей независимых событий как произведение вероятностей отказа ее элементов в течение того же времени:

F_c(t)=F₁(t) F₂(t)...F_i(t)...F_n(t)= 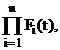(34)

где n - число параллельно соединенных

Рис. 20. Параллельное элементов; F_i(t) - вероятность отказа i-го

соединение элементов элемента системы.

Вероятность безотказной работы сис-

темы в течение времени t при параллельном соединении элементов

P_c(t)=1- F_c(t)=1- 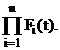(35)

При равнонадежных элементах F_i(t)=F(t), тогда формулы (34) и (35) упрощаются:

F_c(t)= 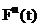, P_c(t)=1- 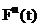. (36)

Из формул (34)-(36) следует, что параллельное соединение элементов является эффективным средством повышения надежности.

Приведенные формулы справедливы только при постоянном резервировании, когда основной и резервный элементы находятся в одинаковых условиях в течение всего времени работы системы.

Соединении элементов

Безотказность объекта при смешанном соединении элементов рассчитываем по приведенным формулам для последовательного и параллельного соединения элементов. Сначала находим вероятность безотказной работы для каждой группы параллельно соединенных элементов по формулам (35) или (36), приводя систему со смешанным соединением к системе с последовательным соединением элементов. Затем определяем вероятность безотказной работы последовательно соединенных элементов по формулам (28) или (30).

Распределения

Интегральная функция экспоненциального распределения по формулам (8) и (37) имеет следующий вид (рис. 22):

F(t)=1-exp(-lt)=1-exp[- ]. (38)

Распределения

Дифференциальная функция (плотность распределения вероятностей) экспоненциального распределения по формулам (12) и (38) имеет вид (рис. 23)

f(t)= l exp(-lt)= exp[- ]. (39)

Распределения

Интенсивность событий экспоненциального распределения выражается уравнением

l(t)= =l= .

Интенсивность событий при экспоненциальном распределении - величина постоянная (рис. 24). Это справедливо только для экспоненциального распределения.

Распределения

Характеристическое свойство экспоненциального распределения состоит в том, что вероятность появления события (отказа объекта, восстановления работоспособности объекта) на интервале времени длительностью Dt не зависит от длительности t предшествующего интервала времени, на котором событие не появлялось, а зависит только от длительности времени Dt при заданной интенсивности событий (рис. 25). Определим вероятность отсутствия событий на этих интервалах времени для экспоненциального распределения.

Вероятность отсутствия события на интервале (0;t+Dt) длительностью t+Dt

P(t+Dt)=exp[-l(t+Dt)]=exp(-lt-lDt)=exp(-lt) exp(-lDt).

Вероятность отсутствия события на интервале (0,t) длительностью t

P(t)=exp(-lt).

Вероятность отсутствия события на интервале (t,t++Dt) длительностью Dt

P(Dt)=exp(-lDt).

Условная вероятность отсутствия события на интервале (t,t+Dt) длительностью Dt, вычисленная в предположении, что событие не появлялось на предшествующем интервале (0,t) длительностью t

P_t(Dt)=