Свойства статически определимых систем

Эти свойства определяются тем обстоятельством, что для нахождения внутренних усилий в таких системах достаточно рассмотреть только уравнения статики (1.10), не обращаясь к геометрическим (1.11) или физическим (1.12) уравнениям.

1) Внутренние усилия не зависят от геометрии поперечных сечений и материала стержней.

Действительно, физические константы E, G, n и геометрические характеристики сечений F, J не входят в уравнения равновесия (1.10).

2) Температурные и кинематические воздействия не вызывают появления реакций и внутренних усилий в СОС.

В самом деле, эти воздействия не входят в правую часть системы алгебраических уравнений для определения опорных реакций (1.6), поэтому они примут вид:

[A] {X} = {0},

откуда следует, что {X} = {0}, так как для СОС det [A] ¹ 0.

3) Если нагрузку, приложенную к какому-либо диску составной системы заменить статически эквивалентной, то реакции и внутренние усилия в остальных дисках не изменятся.

4) Если изменить конфигурацию какого-либо диска составной системы, сохранив расположение опор и соединительных шарниров, то реакции и внутренние усилия в остальных дисках не изменятся.

5) Устранение в СОС любой связи, усилие в которой отлично от нуля, приводит к разрушению всей системы.

Напомним, что неподвижные СОС имеют минимальное число связей, необходимых для их образования, поэтому устранение любой такой связи превращает систему в механизм.

Внутренние усилия в рамах

Определения и порядок построения эпюр

Удобные для применения на практике определения внутренних усилий в рамах – впрочем, они будут справедливы для любых плоских стержневых систем – можно получить естественным обобщением соответствующих определений из сопромата.

Изгибающий момент M в поперечном сечении стержня рамы равен сумме моментов всех сил, взятых по одну сторону от сечения, которое делит раму на две части и вычисленных относительно точки, где сечение пересекает ось стержня.

Поперечная силаQ в поперечном сечении стержня равна сумме проекций на нормаль n к оси стержня всех сил, взятых по одну сторону от сечения, которое делит раму на две части.

Продольная сила N в поперечном сечении стержня равна сумме проекций на касательную t к оси стержня всех сил, взятых по одну сторону от сечения, которое делит раму на две части.

Правило знаков – в соответствии с рис. 2.1, где показан вырезанный двумя сечениями узел рамы.

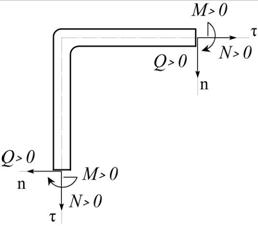
Рис.2.1

Как и в сопромате, положительные значения N соответствуют растяжению стержней, а Q > 0 – вращению рассматриваемого элемента по ходу часовой стрелки. В каждом сечении введена локальная система координат с началом в центре тяжести сечения, орты которой (аналогичные обычным ортам i, j декартовой системы координат) коллинеарны этим усилиям: t­­N, n­­Q. При этом орт n получается из орта tпутем его поворота по ходу часовой стрелки на угол 90°, а положительный изгибающий момент M соответствует повороту от вектора t к вектору n, то есть также направлен по ходу часовой стрелки.

Отметим, что необходимость введения такой локальной системы координат вызвана тем, что для вертикальных стержней рамы становится неопределенным понятие «верхние» и «нижние» волокна. Рассмотренная система отсчета вносит здесь полную ясность: на каждом рассеченном стержне рамы «верх» будет определяться направлением орта n. Нетрудно убедиться, что при этом положительные моменты в сопромате и в строительной механике совпадают и соответствуют растянутым «нижним» волокнам.

Порядок построения эпюр. При построении эпюр внутренних усилий целесообразно придерживаться следующего порядка:

1) определяем опорные реакции;

2) делим раму на участки (i, j), границами которых являются:

- естественные границы рамы, шарниры и угловые точки;

- точки приложения сосредоточенных сил, моментов и границы участков распределенной нагрузки;

3) в пределах каждого участка проводим сечение на расстоянии z_i от его начала и вычисляем значения M, Q, N, рассматривая равновесие отсеченной части рамы;

4) строим эпюры, откладывая положительные значения Q и N на верхних (или левых для вертикальных стержней) волокнах, а M > 0 – на «нижних», то есть в направлении, противоположном нормали n.

5) проверяем правильность построения эпюр:

- рассматривая равновесие вырезанных узлов или других частей рамы;

- контролируя, как и для балок, соблюдение дифференциальных зависимостей Журавского на каждом из ее участков.

Примечания:

1. Поскольку знаки эпюр Q и N привязаны не к локальной, а к глобальной системе координат, ставить знаки у эпюры M не имеет смысла – достаточно знать, что она построена на растянутых волокнах.

2. В строительной механике, в отличие от сопромата, эпюры принято строить именно в такой последовательности: M, Q, N.