Предмет строительной механики и ее задачи

Куликов И.С., Лампси Б.Б.

Статика сооружений: Учебное пособие. – Н.Новгород, Нижегород. гос. архитект. - строит. ун-т, 2012г. – 94 с.

Сжато и доступно изложены основы строительной механики в рамках, не выходящих за пределы требований ГОС. В популярной форме авторы знакомят с основными понятиями и методами этой дисциплины, необходимыми для изучения статически определимых и статически неопределимых плоских стержневых систем. Рассматривается методика построения эпюр внутренних усилий и определения перемещений. Изложен метод сил и метод перемещений, даны сведения о методе конечных элементов. Изложение сопровождается примерами, необходимыми для успешного овладения теорией и приобретения минимальных навыков в решении задач.

Предназначено для студентов направления 521700 - Архитектура, но будет полезно и студентам других специальностей вузов архитектурно-строительного направления, изучающим основы механики или курс статики сооружений по сокращенной программе.

Илл. 66, библиогр. назв.7.

ББК

ISBN ãКуликов И.С., 2012

ãЛампси Б.Б., 2012

ãННГАСУ, 2012

ПРЕДИСЛОВИЕ

Переход к многоуровневой системе образования проходит в условиях гуманитаризации процесса обучения и создания новых информационно-вычислительных систем. Это сопровождается значительным сокращением времени, отводимого на изучение механики у студентов традиционных специальностей, и появлением новых специальностей с одним или двухсеместровым курсом по этой дисциплине.

К их числу относится и курс основ строительной механики для студентов направления 521700 - «Архитектура», который состоит из трех разделов:

- статика твердого тела,

- статика деформируемого тела,

- статика сооружений.

Отметим, что студенты строительных специальностей изучают эти разделы механики в соответствующих курсах: теоретической механики, сопротивления материалов и строительной механики. Поэтому нетрудно понять, что успешное овладение основами механики в рамках сокращенной программы представляет непростую задачу, как для лектора, так и для студентов. И первым шагом на пути её решения является определение целей этого курса. Для студентов-архитекторов они сформулированы так:

- научить анализировать существующие конструктивные решения, понимать работу сооружения в целом и оценивать ту роль, которую играют отдельные элементы ансамбля, устанавливать функциональную связь между воздействиями, внутренними усилиями и формой сооружения;

- способствовать осознанному, свободному и целенаправленному решению основной задачи архитектурного проектирования – поиску новых форм и совершенных решений;

- ознакомить с основными понятиями и методами строительной механики и помочь формированию рационального и логического мышления.

Достижение намеченных целей требует тщательной подготовки учебной программы и её методического обеспечения.

Настоящее пособие является попыткой содействовать решению этой задачи для третьего раздела курса – статики сооружений. Его содержание не претендует на полноту и отражает точку зрения авторов на то, каким должен быть начальный курс этой дисциплины для архитекторов.

В частности, было принято решение ограничиться изучением плоских стержневых систем, которые в пособии представлены балками, рамами, фермами и арками. Изложена методика построения эпюр и определения перемещений, рассмотрены метод сил и метод перемещений. Даны понятия о расчете статически неопределимых систем методом конечных элементов.

Замечания в конце ряда параграфов предназначены для критически настроенных читателей и могут быть оставлены без внимания при первом чтении.

Авторы благодарят студентку факультета архитектуры и градостроительства С. Смирнову за выполненные для этого пособия рисунки.

ГЛАВА 1. ВВЕДЕНИЕ

Связи и их реакции

Напомним, что под связью понимают тело, ограничивающее свободу перемещения выбранного рассматриваемого тела, а реакцией связи называют силу, с которой связь действует на это тело.

Будем называть связь линейной, если соответствующая ей реакция – сила и моментной, если соответствующая ей реакция – момент.

Для плоских стержневых систем можно ограничиться рассмотрением следующих видов связей.

Подвижная опора (рис. 1.1) помимо обозначения по ГОСТу (рис. 1.1, а) может на схемах изображаться так, как показано на рис. 1.1, б и 1.1, в. Она соответствует одной линейной связи, а ее реакция перпендикулярна заштрихованной опорной площадке (рис. 1.1, г).

Рис.1.1

Неподвижная опора (рис. 1.2) также допускает на схемах изображения, отличные от стандартного – на рис. 1.2, а. Очевидно, что она эквивалентна двум линейным связям (рис. 1.2, в – г).

Рис.1.2

Жесткое защемление (рис. 1.3, а) исключает не только перемещения закрепленной точки балки, но и ее поворот вокруг этой точки. Оно эквивалентно двум линейным связям и одной моментной (рис. 1.3, б), либо трем линейным связям при D ® 0 (рис. 1.3, в).

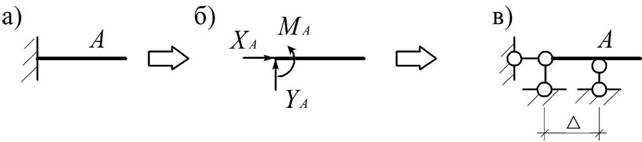
Рис.1.3

Скользящее защемление (рис. 1.4, а – б) в отличие от жесткого не препятствует смещению закрепленной таким образом точки в одном из направлений и эквивалентно линейной и моментной связям (рис. 1.4, в) либо двум линейным при D ® 0 (рис. 1.4, г).

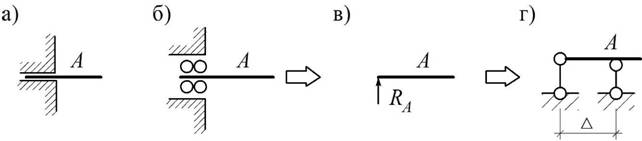
Рис.1.4

Кратный шарнир, соединяющий N дисков, (рис. 1.5, а) эквивалентен (N – 1) простому шарниру (рис. 1.5, б).

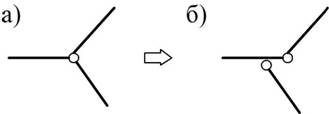
Рис.1.5

Примечания:

1. Результаты расчета можно улучшить, если учесть податливость соединений элементов системы.

2. Построение расчетной схемы действующего сооружения может оказаться непростой задачей, соизмеримой по сложности с самим расчетом.

Внутренние усилия в рамах

Определения и порядок построения эпюр

Удобные для применения на практике определения внутренних усилий в рамах – впрочем, они будут справедливы для любых плоских стержневых систем – можно получить естественным обобщением соответствующих определений из сопромата.

Изгибающий момент M в поперечном сечении стержня рамы равен сумме моментов всех сил, взятых по одну сторону от сечения, которое делит раму на две части и вычисленных относительно точки, где сечение пересекает ось стержня.

Поперечная силаQ в поперечном сечении стержня равна сумме проекций на нормаль n к оси стержня всех сил, взятых по одну сторону от сечения, которое делит раму на две части.

Продольная сила N в поперечном сечении стержня равна сумме проекций на касательную t к оси стержня всех сил, взятых по одну сторону от сечения, которое делит раму на две части.

Правило знаков – в соответствии с рис. 2.1, где показан вырезанный двумя сечениями узел рамы.

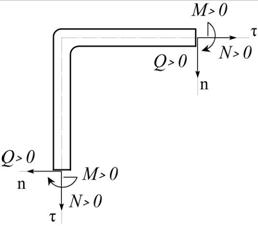
Рис.2.1

Как и в сопромате, положительные значения N соответствуют растяжению стержней, а Q > 0 – вращению рассматриваемого элемента по ходу часовой стрелки. В каждом сечении введена локальная система координат с началом в центре тяжести сечения, орты которой (аналогичные обычным ортам i, j декартовой системы координат) коллинеарны этим усилиям: t­­N, n­­Q. При этом орт n получается из орта tпутем его поворота по ходу часовой стрелки на угол 90°, а положительный изгибающий момент M соответствует повороту от вектора t к вектору n, то есть также направлен по ходу часовой стрелки.

Отметим, что необходимость введения такой локальной системы координат вызвана тем, что для вертикальных стержней рамы становится неопределенным понятие «верхние» и «нижние» волокна. Рассмотренная система отсчета вносит здесь полную ясность: на каждом рассеченном стержне рамы «верх» будет определяться направлением орта n. Нетрудно убедиться, что при этом положительные моменты в сопромате и в строительной механике совпадают и соответствуют растянутым «нижним» волокнам.

Порядок построения эпюр. При построении эпюр внутренних усилий целесообразно придерживаться следующего порядка:

1) определяем опорные реакции;

2) делим раму на участки (i, j), границами которых являются:

- естественные границы рамы, шарниры и угловые точки;

- точки приложения сосредоточенных сил, моментов и границы участков распределенной нагрузки;

3) в пределах каждого участка проводим сечение на расстоянии z_i от его начала и вычисляем значения M, Q, N, рассматривая равновесие отсеченной части рамы;

4) строим эпюры, откладывая положительные значения Q и N на верхних (или левых для вертикальных стержней) волокнах, а M > 0 – на «нижних», то есть в направлении, противоположном нормали n.

5) проверяем правильность построения эпюр:

- рассматривая равновесие вырезанных узлов или других частей рамы;

- контролируя, как и для балок, соблюдение дифференциальных зависимостей Журавского на каждом из ее участков.

Примечания:

1. Поскольку знаки эпюр Q и N привязаны не к локальной, а к глобальной системе координат, ставить знаки у эпюры M не имеет смысла – достаточно знать, что она построена на растянутых волокнах.

2. В строительной механике, в отличие от сопромата, эпюры принято строить именно в такой последовательности: M, Q, N.

Расчет плоских ферм

Основные понятия

Фермойназывается строительная конструкция, образованная из прямолинейных стержней, соединенных идеальными (то есть без трения) шарнирами.

Если нагрузка, приложена только в узлах фермы, образованных этими шарнирами, все стержни будут находиться в условиях центрального растяжения или сжатия.

Напомним, что из внутренних усилий для этого вида напряженно-деформированного состояния отличной от нуля может быть только продольная сила: M = 0, Q = 0, N ¹ 0.

В рамках строительной механики расчет фермы сводится к определению усилий в ее стержнях, и в дальнейшем, при необходимости, к построению эпюры N.

Рассмотрим два простейших метода определения этих усилий.

Метод сечений

Суть этого метода заключается в следующем: проводят сечение, разбивающее ферму на две части и рассматривают равновесие одной из частей под действием: активных сил, опорных реакций и усилий в разрезанных стержнях как произвольной плоской системы сил.

Для такой системы можно составить три уравнения равновесия, поэтому метод удобен, когда сечение пересекает не более трех стержней.

Если все рассеченные стержни при этом непараллельны, то для определения усилий целесообразно составить уравнения:

SM₁ = 0; SM₂ = 0;SM₃ = 0,

взяв в качестве моментных точки, где пересекаются линии действия реакций двух разрезанных стержней из трех, а если два стержня параллельны, то уравнения:

SM₁ = 0; SM₂ = 0;SY = 0,

где ось Oy перпендикулярна этим стержням.

Рассмотренный способ определения усилий можно применять и в том случае, если сечение пересекает более трех стержней, однако при этом каждое из усилий уже не удается найти независимо от остальных, поскольку приходится рассматривать равновесие обеих частей фермы, а иногда - проводить дополнительные сечения.

При решении все стержни фермы рекомендуется считать растянутыми, направляя усилия от узлов.

Пример 2.6. Найти усилия в указанных стержнях фермы (рис. 2.7, а).

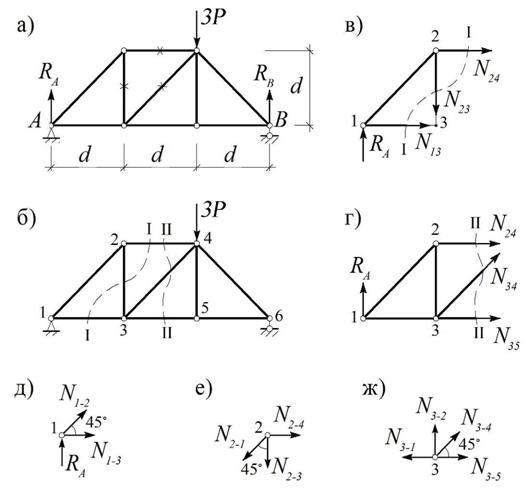
Рис.2.7

Решение. Определяем опорные реакции:

SM_А = 0; _ R_B = 2P;

SM_B = 0; _ R_A = P;

Проверка:

SY = R_A + R_B - 3P = 0.

Для определения усилий N_2-3 и N_2-4 проведем сечение I-I (рис. 2.7, б) и рассмотрим равновесие части фермы, взятой слева от этого сечения. Помимо опорной реакции R_A к ней будут приложены неизвестные усилия в разрезанных стержнях: N_2-4, N_2-3 и N_1-3 (рис. 2.7, в).

Чтобы найти усилие N_2-4 составим уравнение SM₃^(лев) =0, выбрав в качестве моментной точку, где пересекаются линии действия N_2-3 и N_1-3:

-R_A× d - N_2-4 × d = 0; _ N_2-4 = - R_A = - P.

Поскольку стержни 2-4 и 3-5 параллельны и перпендикулярны оси Оу, для нахождения N_2-3 составляем уравнение:

SY ^{( лев)} = R_A - N_2-3 = 0; _ N_2-3 = R_A = P.

Для определения усилия в стержне 3-4 проводим дополнительно сечение II-II, пересекающее этот стержень (рис. 2.7, б) и рассматриваем равновесие части фермы, расположенной слева от этого сечения (рис. 2.7, г):

SY ^{( лев)} = R_A + N_3-4×sin45° = 0; _ N_3-4 = - R_A / sin45° = -P× .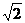

То же самое усилие можно найти, рассматривая равновесие части фермы не слева, а справа от этого сечения:

SY ^{( пр)} = R_В - 3P + N_4-3×sin45° = 0; _ N_4-3 = N_3-4 = -P× . ·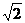

Метод вырезания узлов

Суть этого метода заключается в следующем: рассматривается равновесие вырезанного узла фермы под действием: активных сил, опорных реакций и усилий в разрезанных стержнях как системы сходящихся сил.

Для такой системы сил можно составить только два уравнения равновесия:

SX = 0,SY = 0,

поэтому решение целесообразно начинать с рассмотрения узла, где не более двух неизвестных.

При решении, как и в предыдущем случае, рекомендуется все стержни считать растянутыми, направляя усилия от узлов.

Пример 2.7. Найти усилия в указанных стержнях фермы (рис. 2.7, а), предполагая опорные реакции известными.

Решение. Рассматривая равновесие 1 узла, к которому приложены силы R_A, N_1-2 и N_1-3 , получим (рис. 2.7, б, д):

SY = R_A + N_1-2 ×sin45° = 0; _ N_1-2 = -P× ;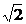

SX = N_1-2 ×cos45° + N_1-3 = 0; _ N_1-3 = P.

Следующим можно рассмотреть узел 2, загруженный неизвестными усилиями N_2-4 и N_2-3 и уже найденным усилием N_2-1 = N_1-2 (рис. 2.7, е):

SX = - N_2-1 ×cos45° + N_2-4 = 0; _ N_2-4 = - P;

SY = - N_2-1 ×sin45° - N_2-3 = 0; _ N_2-3 = P.

Рассматривая, наконец, равновесие третьего узла, загруженного уже найденными усилиями N_3-1 = N_1-3 и N_3-2 = N_2-3, а также неизвестными N_3-4 и N_3-5 (рис. 2.7, е), получим:

SY = N_3-2 + N_3-4×sin45° = 0; _ N_3-4 = -P× .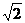

Найденные значения N_2-4, N_2-3 и N_3-4 естественно совпадают с результатами, полученным ранее в примере 2.6. Из второго уравнения находим N_3-5:

SX = - N_3-1 + N_3-4×cos45°+ N_3-5 = 0; _ N_3-5 = 2P.

Эту процедуру можно продолжить и, последовательно рассматривая узлы 4 и 5, определить усилия N_4-5, N_4-6 и N_5-6.

Отметим, что уравнения равновесия для 5 узла будут содержать только одно неизвестное усилие N_5-6, а в уравнения, составленные для последнего 6 узла, вообще войдут только известные величины, поэтому их можно использовать для проверки правильности решения:

SX = - N_6-4 ×cos45° - N_6-5 = 0;

SY = N_6-4 ×sin45° + R_В = 0.

Таким образом, при определении усилий в стержнях фермы методом вырезания узлов три уравнения оказались «лишними».

Полученный результат не является случайным. Мы рассматриваем фермы, которые являются статически определимыми и геометрически неизменяемыми. Для таких ферм выполняется соотношение (1.3):

W* = 2У– С – С_О = 0,

где У - число узлов, С – число стержней фермы, а С_О - число опорных связей, равное трем.

Но поскольку число уравнений для определения усилий в стержнях ферм равняется удвоенному числу узлов, а число неизвестных – числу стержней, то действительно число уравнений всегда на три будет превышать число неизвестных. ·

Примечания:

1. Метод вырезания узлов в отличие от метода сечений является рекуррентным, поэтому ошибка при определении усилия в одном из стержней неизбежно скажется на правильности результата для всех остальных.

2. Рассмотренный метод вырезания узлов можно и целесообразно использовать совместно с методом сечений.

3. Метод можно рассматривать как в аналитической, так и в графической форме.

4. Правильность решения, как и при расчете рам, проверяют, рассматривая равновесие тех узлов или частей фермы, которые не использовались для определения усилий.

5. Во многих случаях расчет фермы удается упростить, если предварительно определить незагруженные или нулевые стержни. Для нахождения таких стержней можно воспользоваться следующими признаками нулевых стержней, справедливость которых легко доказать с помощью метода вырезания узлов:

Признак 1. Усилия в стержнях фермы, образующих незагруженный двухстержневой узел, равны нулю;

Признак 2. Если в загруженном двухстержневом узле линия действия силы совпадает с одним из стержней, усилие во втором стержне равно нулю;

Признак 3. Если в незагруженном трехстержневом узле два стержня расположены вдоль одной прямой, то усилие в третьем стержне равно нулю.

Найденные нулевые стержни можно исключить из фермы вместе с соответствующими шарнирами, упростив тем самым расчетную схему.

Пример 2.7. Найти усилия в указанных стержнях фермы (рис. 2.8, а).

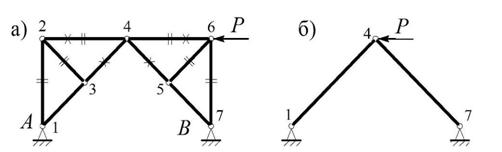
Рис.2.8

Решение. Данная ферма относится к категории арочных, то есть, она образована из двух дисков АС и ВС способом трехшарнирной арки (§1.2.4). Для определения опорных реакций можно воспользоваться уравнениями:

SM_А = 0; _ V_A = Р/2;

SM_B = 0; _ V_В = - Р/2;

SM_C^(AC) = 0; _ H_A = Р/2;

SX = 0; _ H_B = – Р/2.

Однако в данном примере усилия в указанных стержнях фермы можно найти и без определения опорных реакций, если воспользоваться упомянутыми выше признаками нулевых стержней.

В самом деле, рассматривая равновесие 3 узла фермы, найдем, что N_2-3 = 0 (признак 3), поэтому этот стержень можно исключить из фермы вместе с шарниром 3. Тогда N_2-1 = N_2-4 = 0 (признак 1) и эти стержни из фермы также можно исключить.

Аналогично, рассматривая равновесие 5 узла фермы, найдем, что N_5-6 = 0 (признак 3), поэтому этот стержень также можно исключить из фермы вместе с шарниром 5. Тогда, согласно второму признаку, N_6-7 = 0, то есть стержень 4-6 фактически передает нагрузку от 6 узла к узлу 4. Поэтому расчетной схемой фермы служит диада, образованная из двух стержней 1-4 и 4-7, соединенных шарниром 4, к которому приложена сила Р (рис. 2.8, б). Из условий равновесия узла 4, получим:

N_4-1 = - (Р× 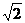)/2;

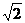N_4-7 = (Р× )/2.

Итак, N_4-2 = N_2-4 = 0, N_4-3 = N_4-1 = - (Р× 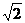)/2. ·

Расчет трехшарнирных арок

Основные понятия

Трехшарнирная арка представляет собой составную систему, образованную из двух дисков, прикрепленных к земле опорными шарнирами А и В и соединенных друг с другом ключевым шарниром С (рис. 2.9, а).

В дальнейшем ограничимся рассмотрением арок, загруженных вертикальной нагрузкой, у которых опорные шарниры находятся на одной горизонтали, а ключевой шарнир расположен симметрично относительно опор.

Расстояние l между опорами арки называется ее пролетом, а высота f_С, на которой расположен соединительный шарнир С – стрелой подъема арки.

Арка является типичным представителем распорных систем, у которых под действием приложенной вертикальной нагрузки появляются не только вертикальные, но и горизонтальные составляющие опорных реакций, называемые распором (рис. 2.9, б).

Определение опорных реакций арки не отличается от определения опорных реакций трехшарнирной рамы (пример 2.5) или арочной фермы (пример 2.7):

SM_А = 0; _ V_В = (1/l) SP_i a_i ;

SM_В = 0; _ V_А =(1/l) SP_i (l - a_i);

SX = 0; _ H_A = H_B = H;

SM_C^(AB) = 0; _ H = H_A = (1/f_С)[V_А×(l/2) -SP_i ( l/2 - a_i)].

Каждой арке можно поставить в соответствие балку с пролетом, равным пролету арки, которая загружена той же нагрузкой, что и арка (рис. 2.9, в). Очевидно, что реакции такой балки будут равны вертикальным реакциям арки:

V_А^Б = V_А; V_В^Б = V_В,

поэтому последнее выражение для распора арки можно записать в виде:

H = M_С^Б/f_С , (2.1)

где M_С^Б = [V_А×(l/2) -SP_i×(l/2 - a_i)] - балочный изгибающий момент под шарниром С, то есть изгибающий момент в сечении x = l/2 соответствующей балки.

Чтобы выяснить, в чем состоит преимущество арки перед соответствующей ей балкой, перейдем к определению внутренних усилий в арке.

Внутренние усилия в арке

Рассмотрим арку в системе координат Оху, где начало отсчета связано с опорой А (рис. 2.9, г) и обозначим через y = f(x) функцию, описывающую очертание оси арки. Проведем сечение на расстоянии х от этой опоры и рассмотрим часть арки слева от сечения.

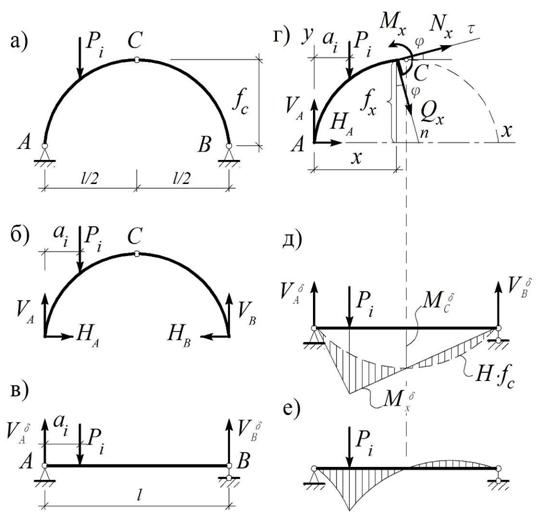
Рис.2.9

Введем локальную систему отсчета с ортами t­­N и n­­Q, и обозначим через j угол, который орт tсоставляет с осьюОх.В отличие от принятого ранее правила (§ 2.2.1) положительным будем считать момент, соответствующий растянутым нижним волокнам арки, то есть так, как принято в сопромате. Это сделано для удобства сравнения изгибающего момента в арке с изгибающим моментом в соответствующей балке.

Из условия равновесия левой части арки получим:

SM ^(лев) = 0; _ M(x) = [V_А×x -SP_i ( x - a_i)] - H× f(x),

или, иначе:

M(x) = M(х)^Б - H×f(x) , (2.2)

где M(х)^Б = [V_А×x-SP_i×(x - a_i)] - балочный изгибающий момент в сечении x.

Последняя формула означает, что при одинаковой нагрузке изгибающие моменты в арке меньше изгибающих моментов в балке соответствующего пролета на величину H× f(x), что наглядно показано на рис. 2.9, д, е.

Это обстоятельство позволяет применять арки для перекрытия больших пролетов – порядка десятков метров. При этом отношение высоты сечения такой арки к длине перекрываемого пролета, как правило, не превышает 1/100. Ни фермы, ни балки не позволяют достичь такого результата.

Для определения поперечной силы в арке составим уравнение:

Sn^(лев) = 0;_ Q(x) = (V_А -SP_i)×cosj - H×sinj,

или, иначе

Q(x) = Q ^Б (x)×cosj - H×sinj , (2.3)

где Q^Б (x) = V_А -SP_i - поперечная сила в соответствующей балке.

Таким образом, при одинаковой нагрузке поперечная сила в арке меньше поперечной силы в балке соответствующего пролета.

Чтобы определить продольную силу составим уравнение:

St^(лев) = 0;_ N(x) = - [(V_А -SP_i)× sinj + H×cosj].

Найденную продольную силу также можно представить в виде:

N(x) = - [Q^Б (x)×sinj + H×cosj]. (2.4)

Последняя формула показывает, что уменьшение изгибающего момента и поперечной силы в арке по сравнению с соответствующей балкой достигается за счет появления продольной силы, которая, как следует из (2.1) будет особенно значительной для арок с небольшим отношением f_C /l.

Таким образом, в арке, как и в раме, в общем случае появляются все три составляющих внутренних усилий: M, Q и N .

Рациональная ось арки

Формула (2.2) показывает, что при заданной нагрузке изгибающие моменты в арке можно уменьшить вплоть до нуля, если соответствующим образом подобрать очертание ее оси.

Определение. Рациональной называется такая арка, изгибающие моменты в которой равны нулю.

Пусть арка с пролетом l и стрелой подъема f_C загружена равномерно распределенной нагрузкой интенсивностью q(x).

Определим очертание рациональной оси такой арки, воспользовавшись соотношением (2.2). Полагая в нем M(x) = 0 , получим:

M(х)^Б - H×f(x) = 0,

откуда найдем искомое уравнение:

y = f(x) = M(х)^Б/ H.

Подставляя сюда выражение изгибающего момента в простой двухопорной балке, загруженной равномерно распределенной нагрузкой:

M(х)^Б = (ql/2)×x - qx²/2

и учитывая, что в силу (2.1) H = М_С^Б/f_С = (ql²)/(8f_С), получим уравнение рациональной оси арки, загруженной равномерно распределенной нагрузкой:

y = f(x) = (4f_С/l²)×(xl - x²).

Как видим, такая арка имеет параболическое очертание.

Примечания:

1. Глобальная система координат Оху, в которой мы рассматриваем арку, не совпадает с локальной системой координат, введенной в § 1.3, поэтому приведенные там основные уравнения строительной механики, включая дифференциальные зависимости Журавского (1.10), в нашем случае выполняться не будут. В частности у рассмотренной арки рационального очертания поперечная сила будет отлична от нуля, несмотря на равенство нулю изгибающего момента.

Это обстоятельство не препятствует определению внутренних усилий и расчету данного класса статически определимых систем на прочность.

2. Что касается перемещений, то в следующей главе будет показано, как перемещения в арке и в других стержневых системах можно найти, не обращаясь непосредственно к основным уравнениям строительной механики.

3. В этом пособии мы ограничимся рассмотрением эпюр внутренних усилий в арке как функций абсциссы х, а не длины дуги s. Отметим, что при этом, в отличие от рам, ось эпюры не совпадает с осью арки.

Интеграл Мора-Максвелла

С помощью (3.15) нетрудно получить формулу для определения перемещения i-ой точки упругой системы от приложенной нагрузки.

Рассмотрим два состояния системы: первое – от заданной нагрузки и второе – от единичной силы или единичного момента, приложенных в точке i в направлении искомого линейного или, соответственно, углового перемещения – (рис. 3.11). Обычно первое из этих состояний называют действительным, а второе – возможным или виртуальным.

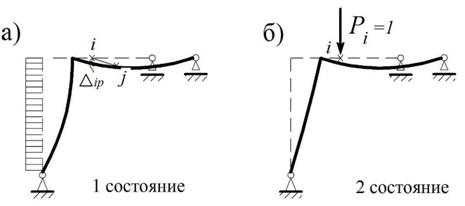
Рис.3.11

Обозначим через D_ip искомое перемещение точки i – в нашем примере на рис. 3.11, а – это вертикальное линейное перемещение.

Пусть M_p, Q_p, N_p – внутренние усилия первого состояния, а`M<sub>i</sub>, `Q_i, `N_i – внутренние силы второго состояния.

Воспользовавшись теоремой Бетти:

A₁₂ = A₂₁,

где

A₂₁ = P_i×D_ip = 1×D_ip = D_ip,

а

A₁₂ = – W₁₂,

получим с помощью (3.15) искомую формулу для определения перемещений, которая называется интегралом Мора-Максвелла:

D_ip = Sò ( M_p`M<sub>i</sub> /EJ + mQ<sub>p</sub>`Q_i /GF + N_p`N_i /EF )ds. (3.16)

Таким образом, для определения линейного (углового) перемещения точки i упругой системы в заданном направлении от заданной нагрузки необходимо:

– построить эпюры M_p, Q_p, N_p в заданной системе от заданной нагрузки;

– построить эпюры `M<sub>i</sub>, `Q_i, `N_i от единичной силы (единичного момента), приложенной в точке i в направлении искомого перемещения;

– вычислить интеграл (3.16).

Отметим, что перемещения в балках и рамах определяются в основном изгибными деформациями, поэтому для таких систем вместо (3.16) можно воспользоваться формулой:

D_ip = Sò ( M_p`M_i /EJ)ds . (3.17)

Наоборот, в фермах отсутствуют изгибающие моменты и поперечные силы, поэтому перемещения здесь полностью определяются продольными деформациями:

D_ip = ò (N_p`N<sub>i</sub> /EF ) ds=S(N<sub>pk</sub> `N_ik /EF_k)l_k, (3.18)

где l_k и EF_k – соответственно длина и продольная жесткость k-го стержня фермы.

Примечания:

1. Вычисление интеграла (3.17) условно называют перемножением эпюр M_p и`M<sub>i</sub> и записывают это в виде: D<sub>ip</sub> = (M<sub>p</sub> ´`M_i).

2. При вычислении перемещений, как правило, пренебрегают деформациями сдвига.

3. При выводе формулы (3.16) нигде не предполагалось, что заданная система является статически определимой, поэтому эта формула верна как для СОС, так и для СНС. Тем не менее, в названии главы фигурируют только СОС поскольку, во-первых, пока в нашем распоряжении нет удобного метода определения внутренних усилий в СНС, а во-вторых, для последних систем формулу (3.16) можно упростить.

Формула Верещагина

Интеграл (3.17) можно вычислить аналитически, однако если жесткости стержней постоянны, удобнее воспользоваться другим способом, который обычно и применяют на практике.

Учитывая, что эпюра`M<sub>i</sub> от единичного силового фактора является кусочно-линейной, можно выбрать промежутки [a,b], где она будет просто линейной. Тогда выбирая начало локальной системы отсчета так, как показано на рис. 3.12, б, ее уравнение можно записать в виде: `M_i(x) = tga×x. При этом интеграл в (3.17) примет вид:

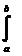( M_p`M_i /EJ)dx = (tga/EJ) 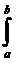x× M_p dx. (3.19)

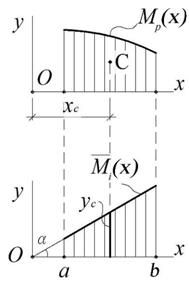
Рис.3.12

Обозначая через w площадь эпюры M_p:

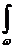w = dw = 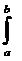M_p dx ,

и учитывая, что ее статический момент относительно оси Oy равен:

S_y = 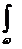xdw = w×x_c,

представим (3.19) в виде:

(tga/EJ) 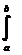x× M_p dx = (tga/EJ) 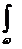xdw= (tga/EJ) x_c×w = (wy_c)/EJ,

где y_c = tga×x_c.

Возвращаясь к формуле (3.17), получим:

D_ip = S (w_ky_ck)/(EJ_k). (3.20)

Таким образом, чтобы перемножить две эпюры, из которых хотя бы одна является линейной, нужно вычислить площадь криволинейной эпюры – w и умножить ее на ординату y_c в линейной эпюре, вычисленную под центром тяжести криволинейной.

Для реализации формулы (3.20) остается рассмотреть геометрические характеристики стандартных эпюр (рис. 3.13), где две последние – соответствуют эпюрам от равномерно распределенной нагрузки. Поскольку любую нестандартную эпюру можно представить комбинацией стандартных, с помощью последних можно перемножить произвольные эпюры.

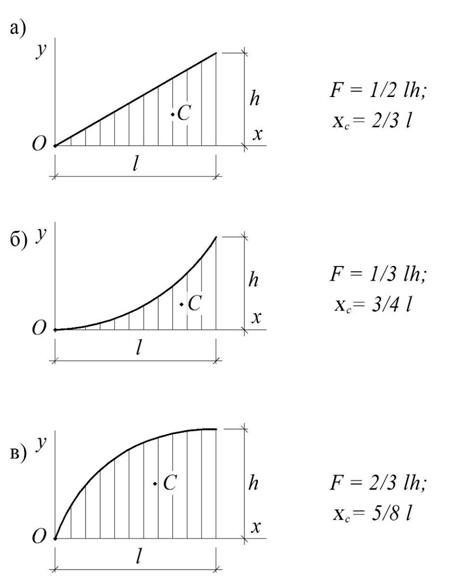
Рис.3.13

Примечания:

1. При выводе формулы (3.20) криволинейная эпюра M_p с площадью w предполагается однозначной. Если это условие не выполнено, ее представляют комбинацией двух или большего числа стандартных эпюр.

2. Для вычисления интеграла (3.17) можно применять формулы численного интегрирования, в том числе – формулу Симпсона:

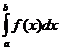= [ (b – a)/6] {f(a) + 4f [ (a + b)/2] + f(b)},

которая позволяет получить точный результат, если функция f (x) является многочленом до третьей степени включительно.

Таким образом, если на всем промежутке [a,b] эпюра `M_i линейна, а эпюра M_p является квадратичной параболой, интеграл (3.17) можно вычислить по формуле:

D_ip=S(l_k/6EJ_k) {M_p(a_k)× `M<sub>i</sub>(a<sub>k</sub>) +4 M<sub>p</sub>[ (a<sub>k</sub> +b<sub>k</sub>)/2]× `M_i[ (a_k+b_k)/2]+M_p(b_k) × `M_i(b_k) }. (3.21)

При этом однозначности эпюры M_p на промежутке [a,b] не требуется, а формулу можно, конечно, применять и для линейной функции M_p(x).

3.7. Примеры определения перемещений

Рассмотрим примеры определения перемещений в СОС от действующей нагрузки. Во всех случаях изгибная жесткость элементов системы – EJ и их продольная жесткость – EF предполагаются известными.

Пример 3.1. Определить максимальные прогибы балки (рис. 3.14, а).

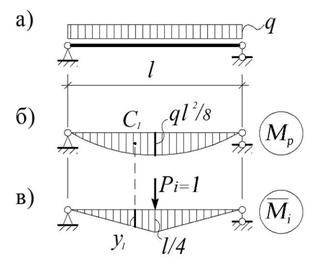
Рис.3.14

Решение. В соответствии с формулой (3.17) строим эпюру M_p от заданной нагрузки (рис. 3.14, б) и эпюру `M_i от единичной силы, приложенной в середине балки (рис. 3.14, в).

Вычислим интеграл (3.17) по формуле Верещагина. На всем промежутке [0,l] эпюра M_p является однозначной, то есть отвечает предъявляемым к ней требованиям, а эпюра`M<sub>i</sub> на всем промежутке [0,l] будет нелинейной. Поэтому область интегрирования делим на два участка: [0, l/2] и [l/2, l], на каждом из которых `M_i(x) будет линейной. С учетом симметрии получим:

v_max = D_ip = 2 (w₁× y_c1)/EJ = 2 [(2/3)×( l/2)×(ql²/8)]×[(5/8)×(l/4)] = 5ql⁴/384EJ.

Для того чтобы