Отыскание параметров выборочного уравнения прямой линии среднеквадратичной регрессии по несгруппированным данным

Пусть изучается система количественных признаков (X, Y). В результате п независимых опытов получены п пар чисел (x₁ y₁), (х₂ y₂),..., (х_п, у_n).

Найдем по данным наблюдений выборочное уравнение прямой линии среднеквадратичной регрессии. Для определенности будем искать уравнение регрессии Y на X: 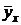=kx + b.

Поскольку различные значения х признака X и соответствующие им значения у признака Y наблюдались по одному разу, то группировать данные нет необходимости. Также нет надобности использовать понятие условной средней, поэтому искомое уравнение можно записать так:

y = kx + b.

Угловой коэффициент прямой линии регрессии Y на X называют выборочным коэффициентом регрессии Y на X и обозначают через r_ух; Итак, будем искать выборочное уравнение прямой линии регрессии Y на X вида

Y = r _ух x + b. (1)

Подберем параметры r_ух и b так, чтобы точки (x₁ y₁),(х₂ y₂),..., (х_п, у_n),построенные по данным наблюдений, на плоскости Оху лежали как можно ближе к прямой (1). Назовем отклонением разность Y_i – y_i (i=l, 2, ..., n), где Y_i –вычисленная по уравнению (1) ордината, соответствующая наблюдаемому значению х_i; у_i – наблюдаемая ордината, соответствующая х_i.

Подберем параметры r_ух и b так, чтобы сумма квадратов отклонений была минимальной (в этом состоит сущность метода наименьших квадратов). Так как каждое отклонение зависит от отыскиваемых параметров, то и сумма квадратов отклонений есть функция этих параметров (временно вместо r_ух будем писать r):

,

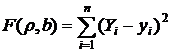или

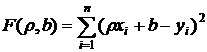
Для отыскания минимума приравняем нулю соответствующие частные производные:

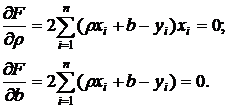
Выполнив элементарные преобразования, получим систему двух линейных уравнений относительно rи b:

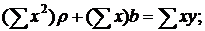
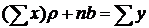. (2)

Решив эту систему, найдем искомые параметры:

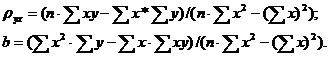(3)

Аналогично можно найти выборочное уравнение прямой линии регрессии X на Y: 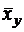= r_xyx + C, где r_ху – выборочный коэффициент регрессии X на Y.

4.4. Корреляционная таблица

При большом числе наблюдений одно и то же значение х может встретиться п_х раз, одно и то же значение у – п_у раз, одна и та же пара чисел (х, у)может наблюдаться п_ху раз. Поэтому данные наблюдений группируют, т. е. подсчитывают частоты п_х, п_у, п_ху. Все сгруппированные данные записывают в виде таблицы, которую называют корреляционной.

Пример.

Y	X
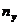0.4 0.6 0.8	–	–	–	–
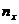					n=60

В первой строке таблицы указаны наблюдаемые значения (10; 20; 30; 40) признака X, а в первом столбце – наблюдаемые значения (0,4; 0,6; 0,8) признака Y. На пересечении строк и столбцов находятся частоты п_ху наблюдаемых пар значений признаков. Например, частота 5 указывает, что пара чисел (10; 0,4) наблюдалась 5 раз. Все частоты помещены в прямоугольнике, стороны которого проведены жирными отрезками. Черточка означает, что соответственная пара чисел, например (20; 0,4), не наблюдалась.

В последнем столбце записаны суммы частот строк. Например, сумма частот первой строки «жирного» прямоугольника равна п_у = 5 + 7 + .14 = 26; это число указывает, что значение признака Y, равное 0,4 (в сочетании с различными значениями признака X), наблюдалось 26 раз.

В последней строке записаны суммы частот столбцов. Например, число 8 указывает, что значение призрака X, равное 10 (в сочетании с различными значениями признака Y), наблюдалось 8 раз.

В клетке, расположенной в нижнем правом углу таблицы, помещена сумма всех частот (общее число всех наблюдений n). Очевидно, 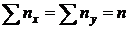. В нашем примере

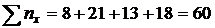и .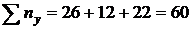

4.5. Отыскание параметров выборочного уравнения прямой линии регрессии по сгруппированным данным

Ранее для определения параметров уравнения прямой линии регрессии Y на X была получена система уравнений

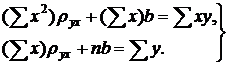(1)

Предполагалось, что значения X и соответствующие им значения Y наблюдались по одному разу. Теперь же допустим, что получено большое число данных (практически для удовлетворительной оценки искомых параметров должно быть хотя бы 50 наблюдений), среди них есть повторяющиеся, и они сгруппированы в виде корреляционной таблицы. Запишем систему (1) так, чтобы она отражала данные корреляционной таблицы. Воспользуемся тождествами:

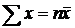(следствие из );

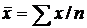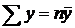(следствие из );

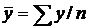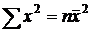(следствие из ),

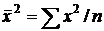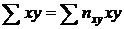(учтено, что пара чисел (х, у)наблюдалась п_ху раз)

Подставив правые части тождеств в систему (1) и сократив обе части второго уравнения на п, получим

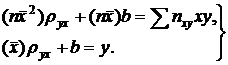(2)

Решив эту систему, найдем параметры r_ху и b и, следовательно, искомое уравнение

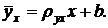(3)

Однако более целесообразно, введя новую величину – выборочный коэффициент корреляции, написать уравнение регрессии в ином виде. Сделаем это. Найдем b из второго уравнения (2):

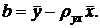
Подставив правую часть этого равенства в уравнение (3), получим

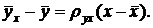(4)

Найдем из системы (1) коэффициент регрессии, учитывая, что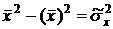

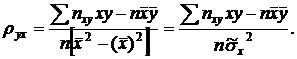
Умножим обе части равенства на дробь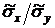

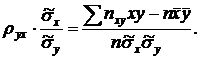(5)

Обозначим правую часть равенства через r_B и назовем ее выборочным коэффициентом корреляции

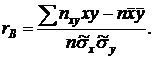
Подставим r_B в (5):

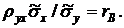
Отсюда

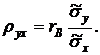
Подставив правую часть этого равенства в (4), окончательно получим выборочное уравнение прямой линии регрессии Y на X вида

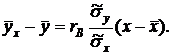
Замечание 1. Аналогично находят выборочное уравнение прямой линии регрессии X на Y вида

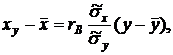
где .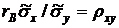

Замечание 2. Уравнения выборочной прямой регрессии можно записать в более симметричной форме:

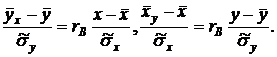
Замечание 3. Можно показать, используя метод моментов, что выборочный коэффициент корреляции является оценкой теоретического коэффициента корреляции