Линейная корреляция. нахождение параметров регрессии,линейный коэффициент корреляции.
Корреляция – это статистическая зависимость между случайными величинами, не имеющими строгого функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.
 варианты зависимостей:1) парная корреляция – связь между двумя признаками (результативным и факторным или двумя факторными); 2) частная корреляция – зависимость между результативным и одним факторным признаком при фиксированном значении других факторных признаков; 3) множественная корреляция – зависимость результативного и двух или более факторных признаков, включенных в исследование.
варианты зависимостей:1) парная корреляция – связь между двумя признаками (результативным и факторным или двумя факторными); 2) частная корреляция – зависимость между результативным и одним факторным признаком при фиксированном значении других факторных признаков; 3) множественная корреляция – зависимость результативного и двух или более факторных признаков, включенных в исследование.
Линейный коэффициент корреляции от –1 до +1. чем к 1, тем теснее связь между признаками. прямой зависимости соответствует знак плюс, а обратной зависимости – знак минус.
Линейным коэффициентом детерминации называется квадрат линейного коэффициента корреляции г2. Его числовое значение всегда заключено в пределе от 0 до 1. Степень тесноты связи полностью соответствует теоретическому корреляционному отношению, которое является универсальным показателем тесноты связи по сравнению с линейным коэффициентом корреляции.
Для того чтобы оценить значимость коэффициента корреляции г, используют f-критерий Стьюдента. Он применяется при f-распределении, отличном от нормального.f-критерий Стьюдента при линейной однофакторной связи рассчитывают по формуле: где (п - 2) — число степеней свободы при заданном уровне значимости а и объеме выборки п.
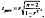
Криволинейная зависимость. Оценка тесноты связи.
Коэффициент корреляции достаточно точно оценивает степень связи лишь в случае наличия линейной зависимости между признаками. При наличии криволинейной зависимости линейный коэффициент корреляции недооценивает степень тесноты связи и даже может быть равен 0, а потому в таких случаях рекомендуется использовать в качестве показателя степени тесноты связи эмпирическое корреляционное отношение.
Множественная корреляция.

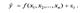
Зависимость между тремя и более признаками называется множественной или многофакторной корреляционной зависимостью. Линейная связь между тремя признаками выражается уравнением:
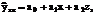
а система нормальных уравнений для определения параметров а0, а1 и а2 будет следующей:
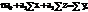
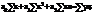
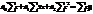
Теснота связи между тремя признаками измеряется с помощью множественного (совокупного) коэффициента корреляции:
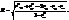 , где
, где 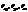 - парные коэффициенты корреляции.
- парные коэффициенты корреляции.
Множественный коэффициент корреляции в квадрате (R2) называется коэффициентом детерминации. Он показывает долю вариации результативного признака, обусловленную вариацией факторных признаков, включенную в регрессионную модель.
