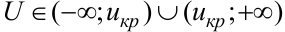Понятие односторонней и двусторонней критической области. Правило нахождения критических точек.

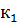Различают одностороннюю(правостороннюю и левостороннюю) и двустороннюю критические области. Правосторонней называют критическую область, определяемую неравенством К> , >0. Левосторонней называют критическую область, определяемую неравенством К< , <0. Двусторонней называют критическую область, определяемую неравенствами К< , К> , > .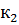

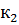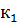Если критические точки симметричны относительно нуля, то двусторонняя

критическая область определяется неравенствами К<- , К> ,, где >0 или что равносильно, /К/> .

Как найти критическую область? К=К(х1,х2,..,хn)-статистический критерий, выбранный для проверки нулевой гипотезы , 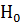, 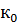– некоторое число, к ∈R. Найдем правостороннюю критическую область, определяемую неравенством К> , где >0. Для ее отыскания достаточно найти критическую точку . Рассмотрим вероятность в Р(К>к) в предположении, что гипотеза 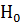верна. Очевидно, что с ростом к0 вероятность Р(К>к) уменьшается. Тогда 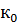можно выбрать настолько большим, что

вероятность Р(К>к) станет ничтожно малой. Другими словами, при

заданном уровне значимости a можно определить критическое значение из

неравенства Р(К>к)=a .

Критическую точку ищут из требования, чтобы при условии справедливости нулевой гипотезы 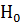вероятность того, что критерий K примет значение, большее , была равна принятому уровню значимостиα: Р(К>к)=a

Для каждого из известных статистических критериев(нормального, Стьюдента, критерия Пирсона , Фишера-Снедекора, Кочрена и др.) имеются соответствующие таблицы, по которым находят , удовлетворяющее этим требованиям. После нахождения по данным выборок вычисляют реализовавшееся(наблюдаемое) значение Кнабл критерия К. Если окажется, что, Кнабл>к , (т.е. реализовалось маловероятное событие), то нулевая гипотеза отвергается. Следовательно, принимается конкурирующая гипотеза .

Если же Кнабл< , то в этом случае нет оснований отвергнуть выдвинутую гипотезу Но . Следовательно, гипотеза Но принимается. Другими словами, выдвинутая статистическая гипотеза согласуется с результатами эксперимента(выборочными данными).

Левосторонняя критическая область определяется неравенством К< , где <0. Критическую точку находят из требования, чтобы при условии справедливости нулевой гипотезы Н0 вероятность того, что критерий К примет значение, меньшее ккр , была равна принятому уровню значимости

α: P(K< )=a. Двусторонняя критическая область определяется неравенствами К<к1, K>k2, где к2>к1.

Критические точки к1,к2 находят из требования, чтобы при условии справедливости нулевой гипотезы сумма вероятностей того, что критерий К примет значение, меньшее к1 или большее к2 , была равна принятому уровню значимости α:Р(К<k1)+P(K>k2)=a. Если распределение критерия симметрично относительно нуля, и для увеличения его мощности выбрать симметричные относительно нуля точки – и , то >0, то P(K<- )=P(K> ), и из Р(К<k1)+P(K>k2)=a следует P(K> )=a/2.Это соотношение и служит для отыскания критических точек двустороннейкритической области.

16 Проверка гипотез о среднем значении нормально распределенной СВ при известной дисперсии
Пусть имеется генеральная совокупность X, распределенная по нормальному закону с известной дисперсией 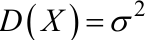(т.е. σ известно). Генеральная средняя a неизвестна, но есть основания предполагать, что она равна предполагаемому значению 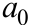. Из нормальной генеральной совокупности X извлечем выборку объема n, по которой найдем 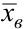. При этом дисперсия 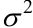известна . Поскольку предполагается, что как СВ 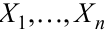взаимно независимы, то они имеют одинаковые нормальные распределения, а следовательно, и одинаковые характеристики ( мат ожидание, дисперсию, и т.д .). Необходимо по известному 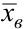при заданном уровне значимости α проверить гипотезу 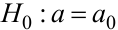о равенстве генеральной средней a гипотетическому значению 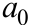. Сформулируем правила проверки гипотезы 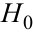обозначив через 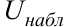значение критерия, вычисленное по данным наблюдений.

Правило 1. Для того чтобы при заданном уровне значимости α проверить гипотезу 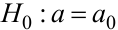о равенстве неизвестной генеральной средней a нормальной совокупности с известной дисперсией 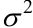гипотетическому значению 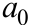при конкурирующей гипотезе 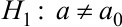, необходимо вычислить 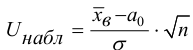(3,5)
и по таблице значений функции Лапласа найти критическую точку двусторонней критической области из равенства 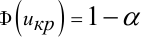(3,6)
Если 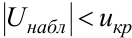– нет оснований отвергнуть гипотезу 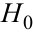; если 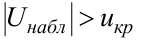– гипотезу 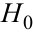отвергают.

Правило 2. При конкурирующей гипотезе 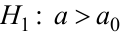критическую точку 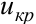правосторонней критической области находят из равенства 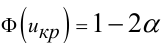(3,7)
Если 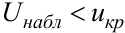– нет оснований отвергнуть гипотезу; если 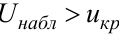– гипотезу 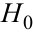отвергают.

Правило 3. При конкурирующей гипотезе 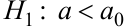критическую точку 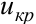находят по правилу 2, а затем полагают границу левосторонней критической области 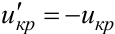. Если 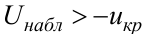– нет оснований отвергнуть гипотезу 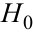; если 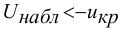– гипотезу 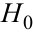отвергают.

Замечание. Из правила 1 следует, что если область принятия гипотезы 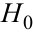есть интервал 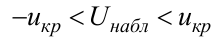, то область ее отклонения –