Определение доверительных интервалов.

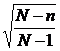- множитель, который корректирует (корректировочный коэффициент)

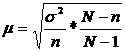- скорректированная на бесповторном отборе ошибка.

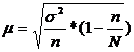
Особенности отбора ошибки выборки при различных видах выборки.

Правило сложения дисперсий использ. Разные виды дисперсий при расчете различных видов выборки.

Правило сложения дисперсий : общая дисперсия это сумма межгрупповой 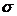и внутригрупповой .

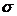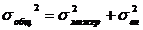
Все виды дисперсии могут быть рассчитаны по аналитической группировке.

Общая дисперсия- 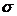признака-резльтата обусловленная вариацией всех признаков влияющих на величину результативного признака.

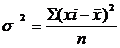
Межгрупповая дисперсия- 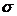признака-резльтата обусловленная вариацией признака-фактора, кот. положен основу группировки

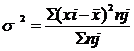
Внутригрупповая дисперсия - 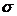признака-резльтата обусловленная прочими факторами, за исключением того фактора кот. Положен основу группировки.

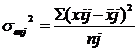
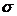каждой j-той группы.

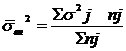
При серийной выборке используют межгрупповую дисперсию.

n- число отобранных серий

При проведении серийной выборки при расчете средней ошибки

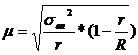
r- число серий отобранных в выборку.

R- число серий выделенных в ГС.

При организации собственно случайной выборки в формуле средней ошибки выборки используют величину общей дисперсии.

При стратифиц. выборке в формуле средней ошибки использ. Величина средней из внутригрупповых дисперсий.

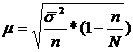
Формула средней ошибки выборочной средней выборочной относит. Величин (доля единиц)

При исследовании альтернативного признака (дихотомическая переменная)

Т.е. единицы совокупности либо обладают данным признаком либо нет.

Опред. доля единиц, которые обладают и не обладают данным признаком.

Виды выборки	Средняя ошибка выборочной средней	Средняя ошибка выбор. Относит. Величины.
Случайная выборка (повторная) отбор единиц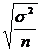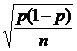
Бесповторная выборка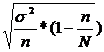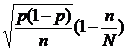
Серийная выборка ( не районированная)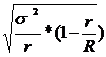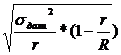
Районированная (стратифицированная) без повтора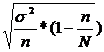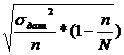
Районированная (серийная) без повтора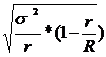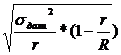

Чтобы понять целесообразность районированного отбора воспользуемся корреляционным отклонением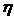

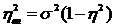
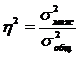
Корреляц Отношение характеризует долю объясненной дисперсии к общей дисперсии.

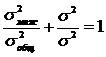
Объясненная дисперсия – дисперсия признака-результата, обусловленная вариацией признака-фактора.

Факторная дисперсия – это дисперсия результативного признака, обусловленная факторами, включенными в анализ, то есть это доля объясненной дисперсии результативного признака.

Остаточная дисперсия – это дисперсия признака-результата, обусловленная факторами, влияние которых не учитывается, то есть не включенными в анализ.

Применение районирования выборки изменять предельную ошибку на 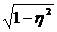и крреляц отношение можно использовать при 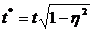корректировки величины .

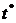Многие выборки формируются как многоступенчатые, их можно представить так:

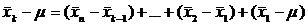
На практике используется

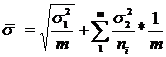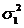где - дисперсия признака х по совокупности.

21.

Расчет объема выборки.

На этапе планирования ВН опред необходимый объем выборочной совокупности.

Формула опред V выборки кот может быть выделена из ф-лы lim ошибки выборки.

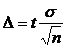
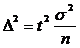
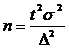
Величина ошибки задается исследователем исходя из цели исследования и специфики изучаемой совокупности и конкретного признака.

Величина t получается из выбранного уровня вероятности.

С повышением уровня доверительной вероятности или уменьшении предельной ошибки выборки предельно допустимой приводит к увеличению V выборки . Не стоит стремиться к высоким цифрам вероятности и минимальной ошибке т.к. получ. При этом большой объем выб. Совокупности может свести к 0 преимущество самого выборочного наблюдения. Величина дисперсии 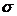в формуле v выборки берется:

1) по результатам предшествующих аналогичных исследований при условии что не изменилось условия существования изучаемойсовокупности, т.е. в самой сов-ти не произошло существенных коренных изменений.

2)Проведение пробного (пилотного) исследования

3)условный расчет величины дисперсии исходя из правила 3-х сигм.

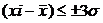
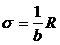
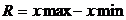
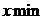
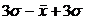
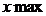
Если в сов-ти заведомо присутствует асимметрия , то величина стандартного отклонения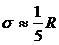

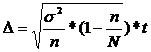
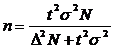- Для бесповторного объема.

Малая выборка.

Большая выборка (БВ) - выборка объемом более 100 единиц.

Малая выборка (МВ)- выборка объемом менее 30 единиц.

При использовании большой выборки независимо от того, как распределены единицы генеральной совокупности (ГС), распределение ошибки выборки всегда подчинено закону нормального распределения.

При расчете предельной ошибки выборки величина t берется из таблицы Лапласа.

Если в генеральной совокупности (ГС) неизвестно распределение единиц генеральной совокупности (ГС), то распределение ошибки выборки подчинено специфическому закону распределения, который был выведен Госсет (Стьюдент).

Т.о. распределение ошибки выборки в условиях малой выборки(МВ) подчиняется закону t- распределение Стьюдента.

t-распределение Стьюдента симметрично, как и нормальное распределение, но его ветви более пологи, т.е. медленнее приближаются к оси ОХ. След-но, t-распределение Стьюдента большее отклонение от центра распределения более вероятны, чем в условиях нормального распределения.

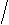
t-распределение Стьюдента

Значения t-распределение Стьюдента табулированы, кодом в таблице является число степеней свободы, d.f.=n-1

t-распределение Стьюдента полностью зависит от объема совокупности и n-объема выборки.

Если сравнивать значения таблиц нормального распределения и t-распре-деление Стьюдента, интегралы Лапласа, то при n³10 значения таблицы Лапласа полностью совпадают.

При n от 30 до 100 значения расходятся несущественно.

При n<30 значительные отличия.

Поэтому малая выборка - выборка объемом менее 30 единиц.

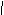При организации малой выборки, при расчете предельной ошибки выборки, величина t берется из таблицы t-распределение Стьюдента.

m=Ös/n

2 2

s=S*(n/n-1)

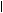
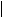При расчете средней ошибки выборки по малой выборки следует сомножитель, с целью корректировки величины выборочной дисперсии.

2

m=Ö(S/n)*(n/n-1)

m=Ö(S/n-1)

Виды связей.

Одна из важнейших задач статистики - измерение взаимосвязей социально-экономических явлений.

Измерение взаимосвязей имеет не только познавательное, но и важное практическое значение, т.к. от объяснения факторов позволяет перейти к управлению ими.

Признак характеризующий следствие - результативный (У).

Признаки характеризующие факторы - факторные (Х).

Главная цель статистического измерение взаимосвязей, обнаружение и количественная характеристика причинно-следственных связей.

Все существующие связи и зависимости делятся на 2 группы:

1- функциональные (жестко детерминированные) связи, когда значению признака-фактора соответствует однозначно определяемая значение признака-результата.

2- статистические (стахостически детерминированные) связи, когда одному значению признака-фактора соответствует множество значений признака-результата, но при этом закономерным образом изменяется среднее значение результативного признака.