Сводка и группировка как этапы статистического исследования.
Статистическая сводка- второй этап статистического исследования, на котором осуществляется сжатие уплотнение исход стат информации. Основным прем сводки- группировка т.е расчленение е.с на отдельные группы по одному или нескольким основным признакам. Признак положен в основу группировки – группировочный признак. Если она проводится по 1-му признаку- простая, если по нескольким признакам – комбинационная. Простая если сов-ть промышленных предприятие разбить по отраслям (признак - отрасль), комбинаторная по формам собственности и размеру отрасли. Учитывая сложность социальной эконом явлений предпочтение следует отдать комбинаторной группировке но при этом необходимо учитывать 2 момента:
1. обозримость таблицы , чем больше кол-во признаков используется в комбинаторной группировки тем менее информативным она становится,
2. наполняемость группировки, группы не должны быть пустыми и малонаполнеными, чем меньше единиц совокупности попадает в выделенные группы, тем менее надежными становятся выводы на основе проведенной группировки.
С помощью группировок решаются 3 основные задачи:
1. выделение объёктивно существующих типов и групп
2. изучение структуры совокупности и структуры сдвигов
3. изучение связи и зависимости
Решение этих задач:
1. решается путем построения типологических группировок
2. с помощью структурной группировки. Оценивают структуру изучаемой совокупности, строиться путем вычисления доли каждого типа или группы в общем объёме совокупности.
3. решается с помощью аналитической группировки. В них в качестве группировочного признака используется признак фактор(факт признак т.е признак изменение которого влияет на изменение другого признака- признака результата) По группам выдел по признаку фактору рассчитывают среднее значения признака рез-та. Вывод о наличие связи м\у признаком фактором и признаком рез-м делается при условии закономерного изменения среднего значений признака рез-та.
На основе аналитической группировки делается вывод о наличие связи или ее отсутствие, о напр-сти зависимости и м.б. рассчитаны показатели тесноты связи (эмпирическое корреляционное отношение и коэффициент детерминации) показатели силы связи.
Некоторые проблемы построения группировок
При построении решаются 3 проблемы:
- выбор группировочного признака
- определение числа выделяемых групп
- для количественных переменных определяется величина интервала группировки.
1- определяется целями и задачами исследования
2- решение связанное с характеров группировочного признака
Если это атрибутивный признак, то число групп соответствует числу имеющихся градаций данного признака
Если признак количественный дискретный и число вариантов значений не велико, то число групп соответствует числу имеющихся вариантов.
Основная проблема выбора числа групп связана с количественным непрерывным признаком. Число групп определяется исходя из предыдущего опыта, интуиции. Может быть использована формализованный подход к определению числа групп при построении группировок, а именно формула Стреджесса.
К=1+3,322*lnN
К - число групп
N – объем совокупности, т.е. число единиц, входящих в совокупность
В этой формуле число групп на прямую зависит от объема совокупности. Она дает хорошие результаты при условии большого объема совокупности.
3 – величина группировочного интервала определяется:
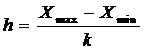
h – величина группировочного интервала
x – max и min значение интервала
k – число групп
Исходя из содержания изучаемой совокупности и сути случайного явления м.б. построены интервалы равные, прогрессивно – возрастающие, прогрессивно – убывающие и специализированные интервалы. Интервалы м.б. открытыми и закрытыми.
6.
Группировка - расчленение единиц совокупности на отдельные группы по одному или нескольким основным признакам. Признак положен в основу группировки – группировочный признак. Если она проводится по 1-му признаку- простая, если по нескольким признакам – комбинационная. Простая если сов-ть промыш предприятие разбить по отраслям (признак - отрасль), комбин по формам собственности и размеру отрасли.Учитывая сложность соц эконом явлений предпочтенее следует отдать комбин групп-ке но при этом необходимо учитывать 2 момента: 1 обозримость табл , чем больше кол-во признаков исп в комбин гр-ки тем менее информ она становится, 2 наполнимость гр-ки, группы не должны быть пустыми и малонаполнеными, чем меньше е.с попадает в выд-ные группы тем менее надежными становятся выводы на основе проведенной групп-ки.
С помощью группировок решаются 3 основные задачи:
1. выделение объёктивно существующих типов и групп
2. изучение структуры совокупности и структуры сдвигов
3. изучение связи и зависимости
Решение этих задач:
1. решается путем построения типологических группировок
2. с помощью структурной группировки. Оценивают структуру изучаемой совокупности, строиться путем вычисления доли каждого типа или группы в общем объёме совокупности.
3. решается с помощью аналитической группировки. В них в качестве группировочного признака используется признак фактор(факт признак т.е признак изменение которого влияет на изменение другого признака- признака результата) По группам выдел по признаку фактору рассчитывают среднее значения признака рез-та. Вывод о наличие связи м\у признаком фактором и признаком рез-м делается при условии закономерного изменения среднего значений признака рез-та.
На основе аналитической группировки делается вывод о наличие связи или ее отсутствие, о напр-сти зависимости и м.б. рассчитаны показатели тесноты связи (эмпирическое корреляционное отношение и коэффициент детерминации) показатели силы связи.
Некоторые проблемы построения группировок
При построении решаются 3 проблемы:
- выбор группировочного признака
- определение числа выделяемых групп
- для количественных переменных определяется величина интервала группировки.
1- определяется целями и задачами исследования
2- решение связанное с характеров группировочного признака
Если это атрибутивный признак, то число групп соответствует числу имеющихся градаций данного признака
Если признак количественный дискретный и число вариантов значений не велико, то число групп соответствует числу имеющихся вариантов.
Основная проблема выбора числа групп связана с количественным непрерывным признаком. Число групп определяется исходя из предыдущего опыта, интуиции. Может быть использована формализованный подход к определению числа групп при построении группировок, а именно формула Стреджесса.
К=1+3,322*lnN
К - число групп
N – объем совокупности, т.е. число единиц, входящих в совокупность
В этой формуле число групп на прямую зависит от объема совокупности. Она дает хорошие результаты при условии большого объема совокупности.
3 – величина группировочного интервала определяется:
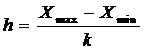
h – величина группировочного интервала
x – max и min значение интервала
k – число групп
Исходя из содержания изучаемой совокупности и сути случайного явления м.б. построены интервалы равные, прогрессивно – возрастающие, прогрессивно – убывающие и специализированные интервалы. Интервалы м.б. открытыми и закрытыми.
