Предмет, метод, задачи статистики

Предмет, метод, задачи статистики

Статистика-наука и искусство сбора, обработки и анализа массовой информации.

«Статистика» имеет несколько значений-

-это система объективной информации о состоянии и развитии соц.-экономических объектов и процессов.

-это особый вид деятельности, связанный со сбором, обработкой и анализом.Система органов статистики всегда государственная. В РФ высший орган- ГОС.КОМ.СТАТ.Остальные органы- в соответствии с территориальным делением РФ. В каждой территориальной еденицы есть комитеты гос. Статистики.

Ежегодно ГОС,КОМ,СТАТОМ разрабатывается программа статистических работ и методологий их проведения. Это позволяет получать сопоставимые показатели, что дает возможность их обобщения на всех уровнях управления. В связи с превращением регионов РФ эк. Самоуправляемые территории возрастает значение региональной статистики.

В иерархии уровней управления региональная статистика занимает промежуточное место между макроэкономической статистикой и статисти-ой фирм.

- статистика, как наука .Это многоотраслевая наука:экономическая и социальная статистика:

ЭКОНОМИЧЕСКАЯ статистика разрабатывает и анализирует макроэк. показатели, и показатели, учитывающие особенности определенных видов деятельности и отдельных отраслей.Состав:

1.статистика промышленности

2.с\х

2.транспорта.

4.банков

5.цен и тарифов

6.финансовая

СОЦИАЛЬНАЯ статистика- статистика народо-населения,здравоохранения, культуры,науки,образования,спорта, туризма.

Эк. и соц.статистика основывается на общих принципах и методах разработки общих теорий статистики.

Общая теория статистики разрабатывает основные принципы и методы сбора, обраб. И анализа информаций.

Общая теория статистики базируется на мат. Статистике и теорий вероятностей.

Предмет статистики- количественная сторона массовых соц.-эк.явлений в неразрывной связи с их качественной стороной,т.е. статистика всегда оперирует цифрами, но в отличии от математических чисел любой статистический показатель отражает качество явления или процесса,т.е. эк-статист. показатель-единство качества и количества.

Объектом изучения статистики выступает статистическая совокупность-это множество однокачественных варьирующих явлений.

Необходимость изучения множества явлений диктуется основной задачей статистики-выявить и дать количественную характеристику закономерности.

В закономерности в отличии от закона проявляется только в массе явлений в виде тенденции.

Методология статистики – совокупность принципов и методов статистического исследования.

Принципы:

1. любое статистическое исследование должно начинаться с глубокого теоретического анализа объекта изучения, т.е. на основе положений экономической науки, нужно определить внутренние и внешние связи и зависимости, факторы, определяющие состоянии и развитие изучаемого объекта или явления. И только после этого выбираются необходимые т возможные методы статистического анализа.
2. опираясь на диалектический метод познания, статистика все изучает в сравнении, во взаимосвязи и в развитии. Исходя из этого статистической наукой разработаны специальные методы, позволяющие проводить анализ по отличительным направлениям.

ЗБЧ

Выявить закономерность при изучении массовых явлений позволяет действия закона больших чисел(ЗБЧ).

СУТЬ закона больших чисел- при расчете показателей по большим совокупностям происходит взаимопогашение индивидуальных различных признаков у единиц совокупности сформированных под влиянием случайных факторов. Их случайность переходит в свою противоположность-необходимость и таким образом в средних величинах, рассчитанных по большим совокупностям, проявляется закономерность, т.е. средние величины - типический уровень признаков в совокупности.

Единица совокупности – предел деления статистической совокупности при условиях сохранения всех её основных свойств. Единицы совокупности являются носителями признаков, которые могут быть классифицированы по разным основаниям.

6.

Группировка - расчленение единиц совокупности на отдельные группы по одному или нескольким основным признакам. Признак положен в основу группировки – группировочный признак. Если она проводится по 1-му признаку- простая, если по нескольким признакам – комбинационная. Простая если сов-ть промыш предприятие разбить по отраслям (признак - отрасль), комбин по формам собственности и размеру отрасли.Учитывая сложность соц эконом явлений предпочтенее следует отдать комбин групп-ке но при этом необходимо учитывать 2 момента: 1 обозримость табл , чем больше кол-во признаков исп в комбин гр-ки тем менее информ она становится, 2 наполнимость гр-ки, группы не должны быть пустыми и малонаполнеными, чем меньше е.с попадает в выд-ные группы тем менее надежными становятся выводы на основе проведенной групп-ки.

С помощью группировок решаются 3 основные задачи:

1. выделение объёктивно существующих типов и групп

2. изучение структуры совокупности и структуры сдвигов

3. изучение связи и зависимости

Решение этих задач:

1. решается путем построения типологических группировок

2. с помощью структурной группировки. Оценивают структуру изучаемой совокупности, строиться путем вычисления доли каждого типа или группы в общем объёме совокупности.

3. решается с помощью аналитической группировки. В них в качестве группировочного признака используется признак фактор(факт признак т.е признак изменение которого влияет на изменение другого признака- признака результата) По группам выдел по признаку фактору рассчитывают среднее значения признака рез-та. Вывод о наличие связи м\у признаком фактором и признаком рез-м делается при условии закономерного изменения среднего значений признака рез-та.

На основе аналитической группировки делается вывод о наличие связи или ее отсутствие, о напр-сти зависимости и м.б. рассчитаны показатели тесноты связи (эмпирическое корреляционное отношение и коэффициент детерминации) показатели силы связи.

Некоторые проблемы построения группировок

При построении решаются 3 проблемы:

1. выбор группировочного признака
2. определение числа выделяемых групп
3. для количественных переменных определяется величина интервала группировки.

1- определяется целями и задачами исследования

2- решение связанное с характеров группировочного признака

Если это атрибутивный признак, то число групп соответствует числу имеющихся градаций данного признака

Если признак количественный дискретный и число вариантов значений не велико, то число групп соответствует числу имеющихся вариантов.

Основная проблема выбора числа групп связана с количественным непрерывным признаком. Число групп определяется исходя из предыдущего опыта, интуиции. Может быть использована формализованный подход к определению числа групп при построении группировок, а именно формула Стреджесса.

К=1+3,322*lnN

К - число групп

N – объем совокупности, т.е. число единиц, входящих в совокупность

В этой формуле число групп на прямую зависит от объема совокупности. Она дает хорошие результаты при условии большого объема совокупности.

3 – величина группировочного интервала определяется:

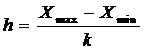
h – величина группировочного интервала

x – max и min значение интервала

k – число групп

Исходя из содержания изучаемой совокупности и сути случайного явления м.б. построены интервалы равные, прогрессивно – возрастающие, прогрессивно – убывающие и специализированные интервалы. Интервалы м.б. открытыми и закрытыми.

Статистические показатели

Сложный характер социально-экономических явлений диктует необходимость расчета системы взаимосвязанных и взаимодополняющих показателей.

Выделяют группы:

1. абсолютные
2. относительные
3. средние величины

АБСОЛЮТЫЕ – показатели характеризующие объем совокупности или отдельных ее типов и групп, а так же объем признака в совокупности или группах.

Первые получаются путем суммирования единиц совокупности, вторые – суммированием значений признаков.

Всегда именованные величины. Несут определенную аналитическую нагрузку, а так же являются базой для расчета относительных и средних характеристик.

ОТНОСИТЕЛЬНЫЕ – м.б. получены путем сопоставления одноименных относительных величин. В результате получаются следующие показатели: показатель динамики, показатель структуры(отношение части к целому), показатель планового задания и выполненного плана, относительный показатель координации(сопоставление частей одного целого), показатель наглядности(сопоставление одноименных показателей в производстве).

Все перечисленные относительные показатели не именованные относительно величины. При сопоставлении разноименных абсолютных величин получают относительный показатель – показатель интенсивности, который характеризует степень распространенности (показатель уровня жизни населения, обеспеченности товарами) – именованные величины.

(8. Типы средних)СРЕДНИЕ ВЕЛИЧИНЫ: необходимо рассчитать средние характеристики обусловленные природой социально-экономических явлений. С одной стороны они устойчивы в массе, с другой стороны – сугубо индивидуальны. Это связано с тем, что формируются они под влиянием множества факторов. Одни из факторов называются основными – определяют типический, характерный для совокупности признак. Другие, случайные факторы, формируют отклонение отдельных значений этого типического уровня. В средних величинах происходит взаимопогашение отклонений, и поэтому средние значения характеризуют типический уровень признака в случайной совокупности. Отражают типический уровень только при условии, что они рассчитаны по однокачественной совокупности явлений и при решении ряда задач необходимым условием является количественная однородность изучаемой совокупности. Средние показатели рассчитываются на единицу совокупности, но характеризуют совокупность в целом. Китле: «Статистические средние представляют собой категорию объективной действительности. Типическое среднее – это истинная величина, отклонение о которой может быть только случайным».

Средние величины м.б. 2-х видов:

1. структурное среднее
2. степенные средние

2-среднее арифметическое, среднее гармоническое, среднее геометрическое, среднее квадратичное.

1-мода и медиана, т.к. их величина не зависит от значения признака по каждой единицы совокупности, а представлена составом(структурой) изучаемой совокупности.

Средняя арифметическая простая:

Таким образом средняя арифметическая это отношение объема признака к объему совокупности. Используется при расчете средних показателей по абсолютным, не сгруппированным данным.

Средняя арифметическая взвешенная:

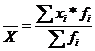
f_i – вес или частота, характеризует как часто в совокупности встречается то или иное значение признака

Среднее арифметическое взвешенное используется при расчете средних характеристик по сгруппированным показателям, а так же для определения средних значений по относительным величинам, при условии, что известен знаменатель исходной формулы усредняемого показателя.

Среднее гармоническое:

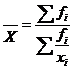
Средне гармоническая величина используется для характеристики типического значения, рассчитанного по относительным показателям, при условии, что известен числитель исходной формулы усредняемого показателя.

Среднее геометрическое:

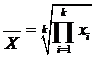k - число сомножителей подкоренного выражения

Используется в анализе рядов динамики при расчете средних темпов роста.

Среднее квадратическое:

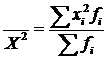
Свойства средней арифметической:

1. Произведение средней арифметической на сумму частот = сумме произведений индивидуальных значений на соответствующие частоты (Средняя арифметическая величина – это значение признака, которым обладала бы каждая единица совокупности, если бы V признака был равномерно распределен в изучаемой совокупности).

2. Сумма отклонений индивидуального значения признака от средней величины всегда =0

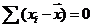Сумма отклонений с “+” и “-” равные

3. Сумма квадратов отклонений индивидуальных значений от средний величины всегда меньше суммы квадратов отклонений индивидуального значения от любой другой положительной величины.

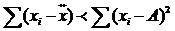
4. Если все значения в совокупности меньше или больше на одну и ту же величину, то средняя арифметическая изменится на эту же величин.

5. Если все частоты или веса меньше или больше на одну и ту же величину средняя арифметическая не изменится.

Показатели вариации

Вариация - различия в индивидуальных значениях признака у единиц совокупности. Наличие вариации и вызывает саму необходимость стат изучения соц-экономических явлений.

Существуют 2 типа показателей вариации:

1 абсолютные

1.1 Размах вариации

R=Xmax-Xmin

Разность между max и min значениями признака.

Он характеризует границы существования признаков совокупности. Прежде чем рассчитывать этот показатель надо оценить изучаемую совокупность на наличие выбросов и может исказить величину этой характеристики.

1.2 Среднее линейное отклонение

d= (Σ |‌‌‌‌‌‌‌‌Xi-X|)/n (по средней арифмет простой)

d= (Σ |Xi - X| fi) / Σ fi (по средней арифмет взвешенной)

Xi- индивидуальные значения признака

1.3 Дисперсия

G² = (Σ (Xi- X) ² fi) / Σ fi ( по средн квад-й)

1.4 Среднее квадратическое

G =√G² = √ (Σ (Xi - X)² fi) / Σ fi

‌Вышеперечисленные показатели, именованные величины измеряются в тех же единицах что и показатель вариации кот изучается.

Показатель дисперсия содержательно не интерпретируется, но используется во многих методах стат. анализа.

В нормально распределенных совокупностях между показателями средняя линейная и средняя квадратическая существует следующее соотношение: G= 1.250 t

Соотношение этих показателей рассчитанных по анализируемой совокупности позволяет предположить наличие или отсутствие эмпирического распределения нормальному.

В нормально распределенной совокупности существуют следующие соотношения между величиной среднего квадратического и числом единиц совокупности.

X+ 1G→68.3%

X+ 2G→95.4%

X+ 3G→99.7%

Это соотношение получило название трех сигм (3-x G) Суть: в совокупности распределения кот соответствует закону нормального распределения, практически не встречаются отклонения превышающие величину 3-х G.

X = 20000

G=1500

3G=4500

18500-21500

15500-24500- предельные изменения признаков совокупности

На основе абсолютных показателей вариации нельзя сравнить степень вариации разных признаков в пределах одной совокупности, а также вариацию одного и того же признака по разным степеням.

2 относительные

Рассчитываются как отношение абсолютных показателей вариации к средней величине по совокупности.

2.1 Коэффициент

Kr= R/X

2.2 Относительное линейное отклонение

Kd= d /X

2.3 Коэффициент вариации

V=G/X

Наиболее аналитические значения имеет коэф вариации. Он чаще всего выражается в %, если он меньше 33 % изучаемая совокупность признается количественно однородной т. е степень разброса значений признака не существенный, если более 33 % совокупность признается неоднородной разброс значений существенный.

Правило сложения дисперсий

Особенности отбора ошибки выборки при различных видах выборки.

Правило сложения дисперсий использ. Разные виды дисперсий при расчете различных видов выборки.

Правило сложения дисперсий : общая дисперсия это сумма межгрупповой 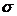и внутригрупповой .

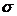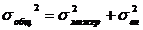
Все виды дисперсии могут быть рассчитаны по аналитической группировке.

Полигон распределения

Этот график классически используется для изображения вариационного ряда построенного по дискретному признаку. Если полигон распределения стремится к интервальному вариационному ряду то в кач-ве варианта используется значение соответствующее серединам интервала.

РИС

Гистограмма

Данный график используется для изображения интервальных вариационных рядов. Основание столбиков соответствуют величине интервала, а высота частоте по каждому интервалу. На гистограмме можно найти значение моды.

Мода - наиболее часто встречающееся значение признаков совокупности.

РИС

Кумулята

Строиться по накопленным частотам или частостям. При построение графика условно нижней границей 1-ого интервала присваивается 0-я частота, верхней границе частота 1-ого интервала, верхней границы 2-ого интервала соответствует накопленная частота 2-ого интервала и тд. При построение кумуляты распределения можно найти значение медианы.

РИС

Расчет объема выборки.

На этапе планирования ВН опред необходимый объем выборочной совокупности.

Формула опред V выборки кот может быть выделена из ф-лы lim ошибки выборки.

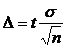
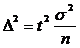
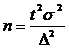
Величина ошибки задается исследователем исходя из цели исследования и специфики изучаемой совокупности и конкретного признака.

Величина t получается из выбранного уровня вероятности.

С повышением уровня доверительной вероятности или уменьшении предельной ошибки выборки предельно допустимой приводит к увеличению V выборки . Не стоит стремиться к высоким цифрам вероятности и минимальной ошибке т.к. получ. При этом большой объем выб. Совокупности может свести к 0 преимущество самого выборочного наблюдения. Величина дисперсии 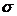в формуле v выборки берется:

1) по результатам предшествующих аналогичных исследований при условии что не изменилось условия существования изучаемойсовокупности, т.е. в самой сов-ти не произошло существенных коренных изменений.

2)Проведение пробного (пилотного) исследования

3)условный расчет величины дисперсии исходя из правила 3-х сигм.

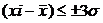
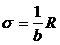
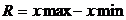
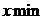
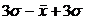
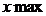
Если в сов-ти заведомо присутствует асимметрия , то величина стандартного отклонения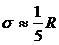

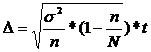
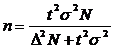- Для бесповторного объема.

Малая выборка.

Большая выборка (БВ) - выборка объемом более 100 единиц.

Малая выборка (МВ)- выборка объемом менее 30 единиц.

При использовании большой выборки независимо от того, как распределены единицы генеральной совокупности (ГС), распределение ошибки выборки всегда подчинено закону нормального распределения.

При расчете предельной ошибки выборки величина t берется из таблицы Лапласа.

Если в генеральной совокупности (ГС) неизвестно распределение единиц генеральной совокупности (ГС), то распределение ошибки выборки подчинено специфическому закону распределения, который был выведен Госсет (Стьюдент).

Т.о. распределение ошибки выборки в условиях малой выборки(МВ) подчиняется закону t- распределение Стьюдента.

t-распределение Стьюдента симметрично, как и нормальное распределение, но его ветви более пологи, т.е. медленнее приближаются к оси ОХ. След-но, t-распределение Стьюдента большее отклонение от центра распределения более вероятны, чем в условиях нормального распределения.

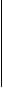
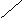
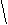
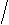
t-распределение Стьюдента

Значения t-распределение Стьюдента табулированы, кодом в таблице является число степеней свободы, d.f.=n-1

t-распределение Стьюдента полностью зависит от объема совокупности и n-объема выборки.

Если сравнивать значения таблиц нормального распределения и t-распре-деление Стьюдента, интегралы Лапласа, то при n³10 значения таблицы Лапласа полностью совпадают.

При n от 30 до 100 значения расходятся несущественно.

При n<30 значительные отличия.

Поэтому малая выборка - выборка объемом менее 30 единиц.

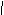При организации малой выборки, при расчете предельной ошибки выборки, величина t берется из таблицы t-распределение Стьюдента.

m=Ös/n

2 2

s=S*(n/n-1)

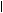
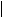При расчете средней ошибки выборки по малой выборки следует сомножитель, с целью корректировки величины выборочной дисперсии.

2

m=Ö(S/n)*(n/n-1)

m=Ö(S/n-1)

Виды связей.

Одна из важнейших задач статистики - измерение взаимосвязей социально-экономических явлений.

Измерение взаимосвязей имеет не только познавательное, но и важное практическое значение, т.к. от объяснения факторов позволяет перейти к управлению ими.

Признак характеризующий следствие - результативный (У).

Признаки характеризующие факторы - факторные (Х).

Главная цель статистического измерение взаимосвязей, обнаружение и количественная характеристика причинно-следственных связей.

Все существующие связи и зависимости делятся на 2 группы:

1- функциональные (жестко детерминированные) связи, когда значению признака-фактора соответствует однозначно определяемая значение признака-результата.

2- статистические (стахостически детерминированные) связи, когда одному значению признака-фактора соответствует множество значений признака-результата, но при этом закономерным образом изменяется среднее значение результативного признака.

Условия применения корреляционно-регрессионного анализа (КРА).

1 - достаточно большой объем статистической совокупности.

2 - объем совокупности должен быть в 6-8 раз (идеально в 10 раз) больше,

числа факторов включаемых в анализ.

3 - изучаемая совокупность должна быть однородна.

4 - признаки включаемые в анализ должны иметь количественное выражение

(возможно включение фиктивных переменных по атрибутивному признаку).

5 - методы корреляции и регрессии ориентированы на закон нормального распределения.

Комплексный корреляционно-регрессионный анализа предполагает:

1 - глубокий теоретический анализ изучаемого объекта или процесса, в ходе которого выявляются внешние и внутренние связи и зависимости, определяются факторы влияющие на состояние и изменение изучаемого объекта.

2 - на основе элементарных статистических приемов выдвигается гипотеза о наличии или отсутствии корреляционной зависимости между исследуемыми признаками.

3 - на основе показателей корреляции делается вывод о наличии или

отсутствии статистически значимых связей и зависимостей.

4 - на основе уравнения регрессии оценивается сила влияния признаков-факторов на результат, осуществляемый ранжирование факторов по силе влияния на результат.

5 - практическое использование результатов КРА и прогнозирование на основе регрессионных моделей.

Перечисленные задачи решаются с использованием корреляции и регрессии.

Поскольку, у этих методов одна общая цель и много общих вычислительных процедур, анализ проводимый с их использованием называется корреляционно-регрессионный анализ (КРА).

Приемами, которыми позволяют выдвинуть гипотезу о наличии или

отсутствии связей:

1 - построение параллельных рядов.

2 - построение групповых и корреляционных таблиц (небольшая

неоднородная групповая таблица).

3 - построение поля корреляции (графическое изображение корреляционной зависимости).

ОХ - значение признака-фактора.

ОУ - значение признака-результата.

. .

. · .

· . · ·

· . .

· ·

Точки на графике соответствуют значению признака-результата при конкретном значении признака-фактора.

На основании изображения поля корреляции, можно сделать предположение о направленности корреляционной зависимости, о наличии или отсутствии связи, а также о степени тесноты корреляционной зависимости, о форме зависимости.

. . . · . · . . · . · . · · · . . ..

. · . · . . · . . · . . · . · . · ·. .

· . · · · . . · . · . · . . .· .· . .· ·.

· . . · . · . · . · . · . . · · ·. . .· ·

· · . . · · · ·. · · ·

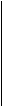
прямая обратная нелинейная зависимость

зависимость зависимость зависимость отсутствует

Практические задачи, решаемые с помощью корреляционно-регрессионный анализа (КРА):

1 - наличие причинно-следственной связи, однозначно определяется зависимая переменная (т.е. признак-результат), и независимая переменная (т.е. признак-фактор).

признак-результат - следствие (объем пр-ва)

признак-фактор - причина (производительность)

2 - наличие взаимосвязи между признаками, изменение одного признака ведет к изменению другого признака, но при этом однозначно не определить, что причина, а что следствие.

3 - наличие ложной корреляции. Ложная корреляция - параллельное изменение двух признаков обусловленное одновременным влиянием на них третьего признака.

Показатели тесноты связи.

Показатели корреляции позволяют подтвердить или опровергнуть наличие корреляционной зависимости между изучаемыми признаками, а также измерить степень тесноты корреляционной зависимости.

Первый коэффициент корреляции - парный коэффициент корреляции Пирсена.

Коэффициент корреляции строится исходя из оценки совместного варьирования двух признаков.

(yi-y)*(xi-x) - среднее произведение этих признаков - ковариация.

Показатель ковариации трудно интерпретировать содержательно, поэтому на практике статистического анализа практически не используется.

Путем стандартизации показатели ковариации получаем коэффициент корреляции Пирсена.

r- коэффициент корреляции Пирсена.

r=[å(yi-y)*(xi-x)/n*6y*6x]

r=(yi*xi-x*у)/(6y*6x)

Парный коэффициент корреляции изменяется в пределах от 0 до 1 по модулю (0£|х|£1)

Коэффициент корреляции может быть отрицательным и положительным.

Знак коэффициента корреляции характеризует направленность зависимостей.

Если коэффициент корреляции отрицательный, то зависимость между изучаемыми признаками обратная.

Если коэффициент корреляции положительный, то зависимость между изучаемыми признаками прямая.

Близость коэффициента корреляции к нулю означает отсутствие связи.

Близость коэффициента корреляции к единице означает, что связь тесная.

Если коэффициент корреляции равен единице, то связь функциональная.

0£|r|£0,3 - связь практически отсутствует

0,3£|r|£0,5 - связь заметная

0,5£|r|£0,7 - связь умеренная

|r|>0,7 - связь тесная

Значимость коэффициента корреляции от объема изучаемых признаков.

(28. Множественный и частный коэффициент)Парный коэффициент корреляции оценивает тесноту связи между парой признаков. При изучении множественной зависимости множественный коэффициент корреляции, кот. характеризует степень тесноты связей между признаком-результатом или некоторыми признаками-факторами.

r - коэффициент детерминации, характеризует долю объясненной дисперсии признака-результата.

Объясненная дисперсия - факторная дисперсия, т.е. дисперсия признака-результата обусловленная вариацией признака-фактора.

r =0,78, т.е. вариация оборота продукции на 78% связано с производительностью труда.

При двухфакторной модели связей множественный коэффициент корреляции - Ry1x1x2

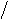2 2 2 2 2 2

Ry1x1x2=Ö(rух1+rух2-2rух1*rух2*rх1х2)/(1-rх1х2)

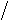Если число анализируемых факторов больше 2, то множественный коэффициент корреляции

2 2

Ry1x1x2xn=Ösф/sобщ

На основе факторной и общей дисперсии.

R - множественный коэффициент детерминации, характеризует долю объемной (факторной) дисперсии, результативного признака в общей дисперсии признака-результата.

Множественный коэффициент корреляции изменяется в пределах от 0 до 1.

При изучении множественной корреляционной зависимости часто возникает необходимость рассчитать частные коэффициенты корреляции, которые оценивают степень тесноты с одним из анализируемым фактором при условии эллеминирования влияния других факторов, включенных в анализ.

Эллеминирование выполняется путем закрепления значений фактора на определенном (как правило на среднем уровне) уровне.

При изучении двухфакторной корреляционной зависимости рассчитывают 2 коэффициента частной корреляции.

2 2

Ryx1,x2=(ryx1-ryx2*rx1x2)/[(1-ryx2)*(1-rx1x2)

Данный коэффициент оценивает тесноту зависимости у от х1 при условии эллеминирования (х2).

2 2

Ryx2,x1=(ryx2-ryx1*rx1x2)/[(1-ryx1)*(1-rx1x2)

Оценивает тесноту связи между (у) и фактором (х2), при условии эллеминирования влияния фактора х(1).

Рассмотренные выше коэффициенты корреляции дают надежные оценки при наличии линейной зависимости между признаком-результатом и признаками-факторами.

Если связь между изучаемыми признаками нелинейная, то при оценке тесноты связи предпочтение следует отдать показателю корреляционному отношению.

Если корреляционное отношение считается по результатам регрессионного анализа, то оно называется теоретическое.

Если по результатам аналитической группировки: эмпирическое.

Теоретическое корреляционное отношение - это отношение факторной дисперсии к общей дисперсии результативного признака.

2 2

h=sфакт/sобщ

2 2

sобщ=å(yi-y)/n

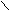2 2

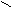
sфакт=å(yi-y)/n

у- теоретическое значение

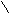
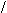2 2

sост=å(yi-y)/n

Остаточная дисперсия - это дисперсия признака-результата обусловленная прочими факторами не включенными в анализ.

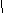
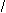
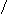2 2

h=Öå(yi-y)/å(yi-y)

Теоретически корреляции изменилась от 0 до1. Чем ближе значение корреляционного отношения к 1, тем теснее зависимость между изучаемыми признаками.

h - коэффициент детерминации и характеризует долю дисперсионного результативного признака, объясненную вариацией анализируемого признака-фактора, т.к. рассчитывается как отношение дисперсии факторной к общей результативного признака.

Эмпирическое корреляционное отношение рассчитывается по данным аналитической группировки, как отношение межгрупповой дисперсии к общей дисперсии результативного признака.

Сравнивая значение коэффициента корреляции с теоретическим корреляционным отношением можно сделать вывод о правомерности использования уравнения линейной зависимости для описания связи между изучаемыми признаками, т.к. в условиях линейной зависимости величина коэффициента корреляции относительно совпадает.

Индекс корреляции (r)- показывает тесноты связи.

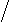2 2

r=Ö1-sост/sобщ

Расчет показателя вариации следует предварять анализам корреляционного поля с целью выявления «выбросов».

Если на поле корреляции выделяются 2 и более группы, то говорят, что в изучаемой совокупности присутствуют кластеринг.

В этом случае совокупность разбивается на группы (кластеринг) показывается корреляции и анализ ведется в разрезе отдельных групп.

Парная линейная регрессия.

Задачи: регрессионный анализ лежит в сфере установленных форм зависимости, определенными факторами регрессии, использования уравнения для оценки неизвестных значений зависимой переменной.

у - признак-результат, зависимая переменная

х - признак-фактор, независимая переменная

Существует достаточно важная характеристика связей с точки зрения в