Воп.22. Парная регрессия на основе метода наименьших квадратов и метода группировок.

Парная регрессия- регрессия между двумя переменными у и х, т.е. модель вида: у = f (x)+E, где у- зависимая переменная (результативный признак); x - независимая, обьясняющая переменная (признак-фактор); E- возмущение, или стохастическая пере­менная, включающая влияние неучтенных факторов в модели. В случае парной линейной зависимости строится регрессионная модель по уравнению линейной регрессии. Параметры этого уравнения оцениваются с помощью процедур, наибольшее распространение получил метод наименьших квадратов.

Метод наименьших квадратов (МНК) - метод оценивания параметров линейной регрессии, минимизирующий сумму квадратов отклонений наблюдений зависимой переменной от искомой линейной функции.

Парная регрессия характеризует связь между двумя признаками - результативным и факторным. Аналитическая связь между ними опи­сывается следующими уравнениями:

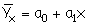прямой

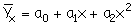гиперболы

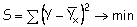параболы и т.д.

Определить тип уравнения можно, исследуя зависимость графи­чески. Однако существуют более общие указания, позволяющие выя­вить уравнение связи, не прибегая к графическому изображению. Если результативный и факторный признаки возрастают одинаково, при­мерно в арифметической прогрессии, то это свидетельствует о том, что связь между ними линейная, а при обратной связи - гиперболи­ческая. Если факторный признак увеличивается в арифметической прогрессии, а результативный - значительно быстрее, то использует­ся связь параболическая или степенная.

Оценка параметров уравнений регрессии (а₀, а₁, и а₂ в уравнении параболы второго порядка) осуществляется методом наименьших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности.

Основной принцип метода наименьших квадратов рассмотрим на следующем примере: будем считать, что две величины (два пока­зателя) X и У взаимосвязаны между собой, причем У находится в не­которой зависимости от Х. Следовательно, У будет зависимой, а Х- независимой величинами.

Сущность метода наименьших квадратов заключается в нахожде­нии параметров модели (а₀, а₁), при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений резуль­тативного признака от теоретических, полученных по выбранному уравнению регрессии: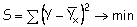

Для прямой зависимости: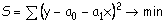

Откуда система нормальных уравнений для нахождения парамет­ров линейной парной регрессии методом наименьших квадратов при­мет следующий вид:

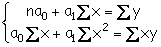
где n - объем исследуемой совокупности (число единиц наблюдений).

В уравнениях регрессии параметр а₀ показывает усредненное вли­яние на результативный признак неучтенных (не выделенных для ис­следования) факторов; параметр а₁ (а в уравнении параболы и а₂) –коэффициент регрессии показывает, насколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.

Применение метода наименьших квадратов объясняется неизбеж­ным наличием случайных ошибок в результатах опыта.

Нахождение уравнения регрессии по сгруппированным данным.Если совокупность сгруппирована по признаку x, для каждой группы найдены средние значения другого признака у, то эти средние дают представление о том, как меняется в среднем у в зависимости от х. Поэтому группировкаслужит средством анализа связи в статистике.

Групповые средние хуже отражают закономерность связи, чем уравнение регрессии, но могут быть использованы в качестве основы для нахождения этого уравнения. Умножая численность каждой группы n_ч на групповую среднюю уч мы получим сумму у в пределах группы Суммируя эти суммы, найдем общую сумму у. Несколько сложнее с суммой ху. Если при сумме ху интервалы группировки малы, то можно считать значение x для всех единиц в рамках группы одинаковым Умножив на него суммуу, получим сумму произведений x на у в рамках группы и, суммируя эти суммы, общую суммуxу. Численность n_x, здесь играет такую же роль, как взвешивание в вычислении средних.