Цифровые комбинационные устройства.

Цифровыми устройствами комбинационного типа или цифровыми автоматами без памяти называются цифровые устройства, логические значения на выходе которых однозначно определяются совокупностью или комбинацией сигналов на входах в данный момент времени. К ним относятся суммирующие схемы, шифраторы и дешифраторы, мультиплексоры и демультиплексоры, цифровые компараторы и другие устройства. Цифровые устройства комбинационного типа выпускаются в виде интегральных микросхем или входят в состав больших интегральных микросхем, таких как процессоры, запоминающие и другие устройства.

Последовательные цифровые устройства. Схемы с памятью.

Цифровые устройства последовательностного типа или цифровые автоматы с памятью — это электронные цифровые устройства, логические значения на выходах которых определяются не только совокупностью логических сигналов на входах в данный момент времени, но и состоянием внутренних элементов памяти по результатам его предшествующей работы. Запоминание предшествующих состояний выполняется при помощи триггеров и регистров памяти.

Типичными примерами логических автоматов с памятью являются счётчики импульсов и сдвиговые регистры.

Схема с памятью – это схема, в которой выходные сигналы Y=(y₁,…,y_m) определяются не только совокупностью входных сигналов X=(x₁,…,x_n), но и совокупностью состояний элементов памяти M=(m₁,…,m_k). Возможность запоминать промежуточные состояния, позволяет использовать информацию для дальнейших преобразований. Получение выходных сигналов в такой схеме происходит с помощью входных сигналов в момент времени t и сигналов элементов памяти в предыдущий момент времени (t-1).

Примерами схем с памятью являются всевозможные последовательные и параллельные регистры, счетчики и др.

В качестве простейшего элемента памяти используют схемы, способные сохранять в течение необходимого времени один разряд двоичного числа (ноль или единицу). В современных ЭВМ таким элементом является триггер. Триггер является основным устройством, способным запоминать информацию. Он имеет два устойчивых состояния – 1 или 0. Наибольшее распространение получили полупроводниковые триггеры, выпускаемые в виде интегральных микросхем и представляющие собой двухкаскадные усилители постоянного тока с положительной обратной связью.

Математическая модель микропроцессора

Система автоматического управления, блок управления которой выполнен в виде микропроцессорной системы, является дискретной САУ. Из курса ТАУ известно, что математическая модель дискретной САУ выглядит следующим образом (рис. 1):

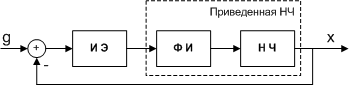Рис. 1.

Однако корректное использование математической модели цифровой системы невозможно, если неизвестно точное соответствие частей модели структурным единицам и блокам МПС. Обобщенная структурная схема МПС представлена на рис. 2.

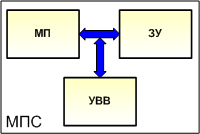Рис. 2.

На первый взгляд, соответствие структурной схемы (рис. 2) и математической модели (рис. 1) не просматривается. Попробуем его найти.

Рассмотрим частный случай цифровой САУ — цифровой электропривод (рис. 3):

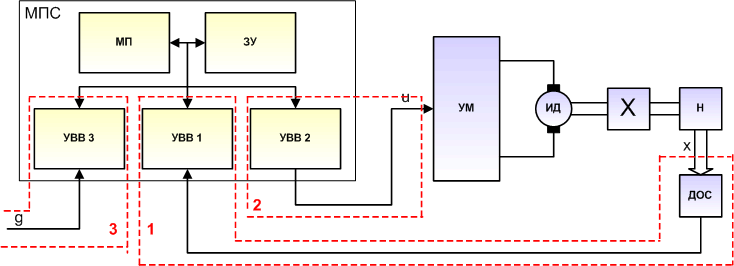Рис. 3.

Как видно, САУ состоит из микропроцессорной системы (микропроцессор, запоминающее устройство и 3-х УВВ) и непрерывной неизменяемой части (усилитель мощности, исполнительный двигатель, редуктор, нагрузка и датчик обратной связи). Выделим в этой системе четыре элемента:

1. Канал обратной связи (УВВ 1, ДОС и линии связи);

2. Канал управляющих сигналов (УВВ 2 и линии связи);

3. Канал входных сигналов (УВВ 3 и линии связи);

4. Цифровой фильтр (микропроцессор и запоминающее устройство).

Таким образом, МПСУ состоит из цифрового фильтра, трех каналов связи и непрерывной неизменяемой части.

Почему микропроцессор и запоминающее устройство названы цифровым фильтром? В технике принято называть фильтром любое устройство, если при прохождении через него синусоидального сигнала амплитуда этого сигнала меняется. Любое корректирующее устройство представляет собой фильтр. В запоминающем устройстве хранится программа, реализующая алгоритм управления, а следовательно – осуществляющая фильтрацию сигналов, проходящих через МПС. Эта фильтрация называется цифровой, поскольку микропроцессор выполняет команды за конечное время и работает с дискретными величинами. Имеет место квантование по времени и по уровню. Следовательно, микропроцессор работает как цифровой фильтр.

Рассмотрим более подробно структуру трех перечисленных каналов связи и попытаемся получить их математическое описание.

Канал обратных связей (КОС)

Согласно схеме, приведенной на рис. 3. КОС имеет следующую структуру (рис. 4):

Рис. 4.

Здесь Д— датчик обратной связи. Датчик может быть непрерывным и дискретным. Рассмотрим эти два варианта отдельно.

КОС с непрерывным датчиком

В этом случае датчик может быть представлен в виде усилительного звена с некоторым коэффициентом усиления, которое путем структурных преобразований может быть перенесено в прямую цепь контура САУ. В результате структура КОС оказывается следующей (рис. 5):

Рис. 5.

Здесь 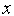— сигнал обратной связи, приходящий с датчика, 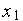— данные, передаваемые по шине данных и представленные в числовом виде. Из-за ограниченности разрядной сетки число 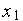не может принимать любые значения в диапазоне своего изменения, имеет место квантование по уровню. Следовательно, КОС должен содержать устройство, обеспечивающее квантование сигнала по уровню. Такое устройство называется аналого-цифровым преобразователем (АЦП).

Блок-схема алгоритма управления для цифровой системы имеет вид (рис. 6):

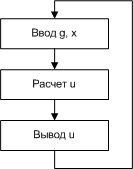Рис. 6.

Так как каждый шаг алгоритма состоит из набора команд микропроцессора и выполняется за конечное время, ввод сигнала 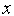производится в дискретные моменты времени, отстоящие друг от друга на величину 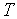, которая равна общей длительности выполнения одного цикла алгоритма управления. Следовательно, сигнал 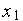(см. рис. 5) квантован по времени. Поэтому в математической модели КОС должен присутствовать импульсный элемент, отражающий факт квантования сигнала по времени (рис. 7).

Рис. 7.

Здесь 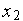— сигнал, квантованный по уровню, 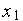— сигнал, квантованный по времени и уровню. Схема на рис. 7 представляет собой математическую модель канала обратной связи с непрерывным датчиком.

Следует обратить внимание, что физически импульсного элемента не существует. Присутствие его в математической модели лишь отражает факт квантования сигнала по времени. Физически это квантование осуществляет сам микропроцессор, выполняя ввод данных в дискретные моменты времени.

КОС с дискретным датчиком

В дискретном датчике преобразование непрерывного сигнала в дискретный и соответствующее квантование по уровню происходит внутри самого датчика, сигнал на его выходе представляется уже в цифровом виде. Поэтому мы можем рассматривать дискретный датчик как АЦП, понимая под АЦП здесь любое устройство, осуществляющее квантование по уровню. Следовательно, в случае дискретного датчика КОС также описывается схемой, представленной на рис. 7.

АЦП и его характеристики

Обычно АЦП рассматривают как статический элемент, то есть предполагают, что запаздывание сигналов, проходящих через него, очень мало. Однако в высокоскоростных системах приходится учитывать конечность времени преобразования в АЦП непрерывного сигнала в соответствующий цифровой код.

Реальный АЦП имеет следующую характеристику (рис. 8):

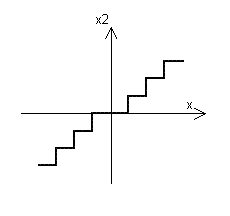Рис. 8.

То есть он является нелинейным элементом. Горизонтальный размер ступеньки на характеристике называется ценой младшего разряда АЦП ( 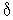). Чем меньше цена младшего разряда, тем большее число разрядов двоичного числа необходимо для представления преобразованного значения при одном и том же диапазоне его изменения. На практике цена младшего разряда выбирается исходя из максимально допустимой ошибки (они должны быть примерно равны): .

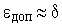Наличие нелинейного элемента в цепи обратной связи будет приводить к возникновению автоколебаний, амплитуда которых сравнима с ценой младшего разряда АЦП. Однако колебания могут демпфироваться силами трения в опорах, которые играют роль нелинейного элемента с зоной нечувствительности. На практике, для того, чтобы уйти от эффекта автоколебаний, увеличивают разрядность АЦП на 2-3 разряда по сравнению с той, которая необходима для обеспечения требуемой точности системы. В расчетах часто используется линеаризованную статическую характеристику АЦП, представляя его усилительным звеном с коэффициентом усиления .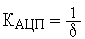

Подобная линеаризация оправдана при условии большого количества разрядов АЦП и малого значения 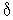.Влияние нелинейных факторов на работу скорректированной системы оценивается отдельно.

Канал входных сигналов

Если сигнал g подается на вход МПСУ в непрерывном (аналоговом) виде, структура канала входных сигналов (КВС) такая же, как и КОС (рис. 7).

Если же входной сигнал передается от другой МПС (ЭВМ), на первый взгляд он является сразу квантованным по уровню, и АЦП в канале не нужен. Но, принимая во внимание, что по своей физической сути сигнал 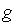– непрерывная величина (мы рассматриваем цифровой привод), можно сказать, что квантование по уровню все равно имело место (было выполнено в ЭВМ верхнего уровня), а, следовательно, математическая модель КВС должна содержать АЦП (хотя физически — как отдельного устройства — его нет).

Таким образом, КВС описывается следующей схемой (рис. 9):

Рис. 9.

Здесь 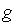— непрерывный входной сигнал, 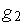— входной сигнал, квантованный по уровню, 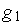— входной сигнал, квантованный по уровню и времени.

Канал управляющих сигналов

На входе этого канала (КУС) всегда находится сигнал, квантованный по уровню. На вход усилителя мощности необходимо подавать непрерывный сигнал. Следовательно, сигнал должен быть преобразован из квантованного по уровню в непрерывный. Для этого используется цифро-аналоговый преобразователь (ЦАП). Под ЦАП будем понимать любое устройство, преобразующее квантованный по уровню сигнал в непрерывный.

Кроме этого, выдача сигнала происходит в дискретные моменты времени в соответствии с алгоритмом работы МПС (см. рис. 10).

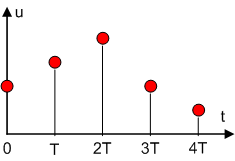Рис. 10.

Выдача сигнала на усилитель мощности в дискретные моменты времени может привести к появлению высокочастотных колебаний в приводе. Следовательно, выдаваемый сигнал должен присутствовать на выходе и в промежутках между выдачами рассчитанного значения. Для этой цели используется экстраполятор — устройство, преобразующее сигналы, дискретные по времени, в непрерывные. Наиболее часто применяются в МПС экстраполяторы нулевого порядка, заполняющие интервал постоянным значением (рис. 11):

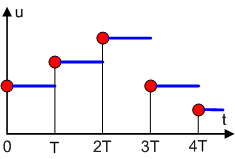Рис. 11.

Экстраполятор нулевого порядка технически может быть реализован в виде регистра, хранящего последнее рассчитанное значение.

Таким образом, канал управляющих сигналов может быть описан следующей структурной схемой:

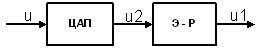Рис. 12.

Здесь 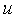— сигнал, квантованный по времени и уровню, 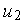— сигнал, квантованный по времени, 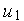— непрерывный сигнал на выходе канала.

ЦАП и его характеристики

Цифро-аналоговый преобразователь имеет нелинейную характеристику, аналогичную АЦП (рис. 8). Все рассуждения, проводившиеся для АЦП относительно возможности возникновения автоколебания и выборе цены младшего разряда, справедливы и для ЦАП. При расчетах он также условно представляется линейным элементом (усилительным звеном) с коэффициентом усиления .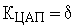

Математическая модель МПСУ

Теперь, когда мы нашли описания всех каналов связи, представим их на единой структурной схеме, взяв за основу структурную схему МПСУ (рис. 13).

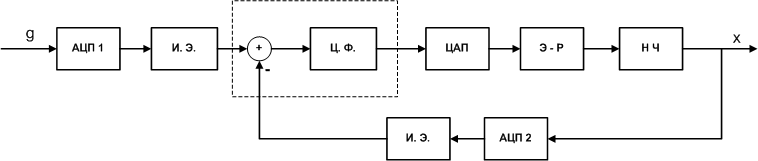Рис. 13.

Операция вычисления ошибки реально выполняется микропроцессором (цифровым фильтром) в соответствии с алгоритмом управления. На приведенной выше схеме она вынесена за пределы ЦФ исключительно для удобства моделирования МПС (физически представленный на схеме сумматор не существует).

АЦП 1 и АЦП 2 имеют разрядност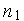и и 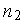соответственно. На практике, как правило, их разрядности совпадают, так как в противном случае при вычислении ошибки неизбежно будет возникать погрешность. Поэтому мы тоже можем допустить, что разрядности АЦП 1 и АЦП 2 совпадают.

Рассмотрим теперь работу во времени импульсных элементов в каналах ОС и ВС.

Времена их срабатывания соответствуют моментам ввода сигнала 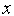и сигнала 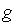(рис. 6). Если предположить, что время выполнения расчета намного больше, чем время ввода 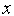и 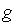(а так и бывает в большинстве случаев), можно считать, что импульсные элементы срабатывают одновременно (то есть работают синхронно и синфазно).

С учетом приведенных рассуждений, схема рис. 13 может быть преобразована к следующему виду (рис. 14):

Рис. 14.

Представим АЦП в виде усилительного звена с коэффициентом усиления 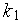, ЦАП — в виде усилительного звена с коэффициентом усиления 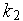. Тогда при условии, что в ЦФ реализуются линейные алгоритмы коррекции, схема рис. 14 может быть представлена в следующем виде (рис. 15):

Рис. 15.

Если пренебречь известным эффектом реализации линейных корректирующих устройств в МПС, когда дискретная реализация дает заведомо худшие показатели качества СУ, можно заменить ЦФ неким непрерывным корректирующим устройством, присоединенным к непрерывной части системы. С учетом того, что экстраполятор — то же самое, что и формирователь импульса, получим из рис. 15 следующую модель (рис. 16):

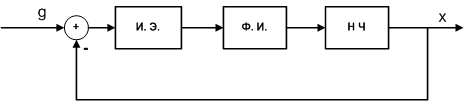Рис. 16.

Таким образом, мы пришли к классической математической модели дискретной САУ (рис. 1).

Еще раз повторим тем допущения, которые были сделаны при нахождении математической модели МПСУ:

1. Разрядности АЦП в каналах ОС и ВС одинаковы.

2. Пренебрегаем нелинейностью характеристик ЦАП и АЦП, заменяя их линейными усилительными звеньями.

3. Ввод данных в микропроцессор происходит намного быстрее, чем расчет управляющего сигнала, поэтому срабатывание импульсных элементов в каналах ОС и ВС можно считать одновременным.

4. В цифровом фильтре реализованы линейные алгоритмы управления.