Какой смысл коэффициента эксцесса.

Характеризует меру затянутости хвостового распределения.

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНОГО ВЕКТОРА.

Как определяются начальные моменты случайного вектора?

α_{k1, k2,..., kn}(x₁, x₂,..., x_n)=

=M(x₁^k1 x₂^k2... x_n^kn)

Как определяются центральные моменты случайного вектора?

X^○=X-M(X)

μ(k₁, k₂,..., k_n)=M((x₁^○)^k1(x₂^○)^k2...(x_n^○)^kn)

Записать формулы для вычисления начальных моментов двумерных дискретных случайных величин.

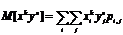
Записать формулы для вычисления начальных моментов двумерных непрерывных случайных величин.

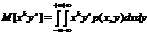
Чему равны начальные и центральные моменты нулевого порядка двумерной случайной величины?

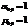
Чему равны начальные и центральные моменты первого порядка двумерной случайной величины?

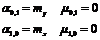
Чему равны центральные моменты второго порядка двумерной случайной величины?

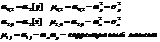
Дать определение корреляционного момента.

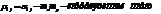Корреляционный момент характеризует степень тесноты линейной зависимости величин X и Y и рассеивание их значений относительно точки (m_X, m_Y).

Перечислить основные свойства корреляционного момента.

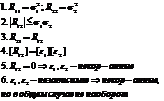
Записать формулу для вычисления корреляционного момента дискретных случайных величин.

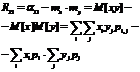
Записать формулу для вычисления корреляционного момента непрерывных случайных величин.

?

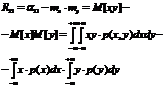Чему равна дисперсия суммы двух случайных величин?

D(x+y)=M((x+y)²)-M²(x+y)= =M(x²)+2M(xy)+M(y²)-(M(x)+M(y))²= =D(x)+D(y)+2R₁₂,

где R₁₂ – корреляционный момент

Чему равно математическое ожидание произведения двух случайных величин?

M(xy)=M(x)M(y)+R₁₂,

где R₁₂ – корреляционный момент

Как связаны понятия независимости и некоррелированности случайных величин? Ответ обосновать.

Если величины независимы – они некоррелированы, но обратное в общем случае неверно:

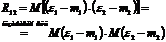
Дать определение коэффициента корреляции.

Коэффициент корреляции 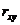характеризует степень линейной зависимости величин и равен: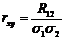

Перечислить основные свойства коэффициента корреляции.

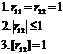
В каких границах могут находиться значения корреляционного момента и коэффициента корреляции?

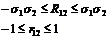
Чему равен коэффициент корреляции двух случайных величин, связанных линейной зависимостью?

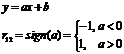
Каков смысл корреляционного момента и коэффициента корреляции?

Корреляционный момент характеризует степень тесноты линейной зависимости величин X и Y и рассеивание их значений относительно точки (m_X, m_Y). Коэффициент корреляции 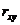характеризует степень линейной зависимости величин.

Дать определение корреляционной матрице. Какие у неё свойства?

Корреляционной матрицей называется матрица такого вида:

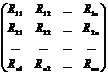
со следующими свойствами: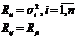

Дать определение матрице коэффициентов корреляции. Какие у неё свойства?

Матрицей коэффициентов корреляции называется матрица такого вида:

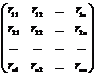со следующими свойствами: ?

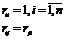ОСНОВНЫЕ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН.