Диаграмма предельных амплитуд
Для построения диаграммы предельных амплитуд необходимо иметь пределы выносливости при различных значениях параметра “ 
” (коэффициент асимметрии). Введение значительно усложняет эксперимент, т.к. теперь уже необходимо иметь несколько десятков образцов, каждый десяток из которых испытывается при 
. Задавая постоянное значение 
, находим путем последовательных испытаний образцов такое наибольшее значение амплитуды, при котором материал способен еще выдержать неограниченное число циклов. В результате испытаний одного десятка образцов получаем одну точку на диаграмме предельных амплитуд. Произведя испытания следующей группы образцов, мы получаем еще одну точку и т.д. (рис.11.7).
Рис. 11.7
Смысл диаграммы предельных амплитуд очевиден. Пусть цикл характеризуют напряжения 
и , которые будем рассматривать как координаты рабочей точки. Нанеся рабочую точку на диаграмму, мы можем судить о прочности образца. Если рабочая точка располагается ниже предельной кривой, то образец выдержит бесконечно большое число циклов (не менее базового). Если Р.Т. находится выше кривой, то образец разрушится при каком-то числе циклов, меньшем базового.
Построение диаграммы предельных амплитуд 
очень трудоемко, поэтому ее часто схематизируют отрезками прямых. Точка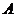 
отражает соответствующее испытание образцов при симметричном цикле. Точка 
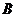соответствует статическому испытанию образцов. Для хрупких материалов она определяется по пределу прочности 
. Для пластичных материалов ограничение может быть как по пределу текучести 
, так и пределу прочности .
Для построения левой части диаграммы нужна еще хотя бы одна точка, например, для пульсационного цикла, либо знать угол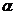 
наклона прямой. Введем понятие углового коэффициента 
= 
. Опытами доказано, что значение углового коэффициента для углеродистых сталей лежит в пределах 0,1÷0,2 и для легированных 0,2÷0,3.
Таким образом, уравнение левой прямой имеет вид 
. Правая часть диаграммы аппроксимируется прямой, проходящей через точку 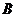и составляющей угол 45 
с осями и
Следовательно, при схематизации диаграмма предельных амплитуд, заменяется двумя прямыми 
и 
.
Построенная диаграмма пока не позволяет рассчитывать детали на прочность, т.к. усталостная прочность зависит еще от многих факторов. 
Факторы, влияющие на усталостную прочность
Концентрация напряжений
Концентрацией называют явление скачкообразного увеличения напряжений вблизи резких смен формы детали, отверстий, выточек (Рис. 11.8)
Рис. 11.8
Мерой концентрации является теоретический коэффициент концентрации напряжений равный:
при растяжении, изгибе, 
при кручении,
— так называемое номинальное напряжение, определяемое по формулам сопротивления материалов, 
— наибольшее местное напряжение. Данные о теоретическом коэффициенте концентрации напряжений приводятся в справочниках по машиностроению. Концентрация напряжений оказывает на прочность детали различное влияние в зависимости от свойств материала и условий нагружения. Поэтому вместо теоретического коэффициента концентрации напряжения 
вводят эффективный коэффициент концентрации напряжений 
и 
.
Для симметричного цикла эффективный коэффициент концентрации напряжений определяют отношением
,
где 
— пределы выносливости гладкого образца,
— пределы выносливости подсчитанных по номинальным напряжениям для образцов, имеющих концентрацию напряжения, но такие же размеры поперечного сечения как и у гладкого образца. 
определяют по таблицам.
В тех случаях, когда нет экспериментальных данных, по прямому определению и прибегают к приближенным оценкам. Например, по формуле
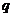— коэффициент чувствительности материала к концентрации напряжений. Он зависит в основном от материала. Для конструкционных сталей 
.
Масштабный эффект
Если из одного и того же материала изготовить несколько образцов разного диаметра, то после испытания на усталость можно обнаружить, что предел выносливости с увеличением диаметра уменьшается. Снижение предела выносливости с увеличением размеров детали получило название масштабного эффекта.
Мерой этого понижения служит коэффициент масштабного фактора
; 
, где
— предел выносливости образца с диаметром, как и деталь
— предел выносливости образца d=7,5мм.
На рис. 11.9 дается ориентировочная зависимость масштабного фактора от диаметра вала для случая изгиба и кручения.
Рис. 11.9
Кривая 1 получена для углеродистой стали, 2 — для легированной.