Потенциальная энергия деформации

Рассмотрим процесс деформирования упруго тела с энергетической точки зрения. Внешние силы, приложенные к упругому телу, совершают работу — 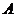. В результате этой работы накапливается потенциальная энергия — 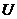. Также работа идет на сообщение скорости массе тела, т.е. кинетической энергии .

.

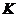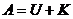Если скорость неограниченно мала, т.е. процесс статический, то

.

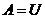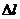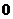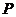Поскольку на пути сила меняется от до (рис. 2.5), то работа должна быть определена интегрированием по элементарным участкам пути.

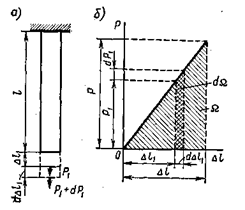
Рис. 2.5

На элементарном пути 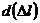работа текущей силы 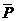равна .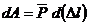

Очевидно, работа на перемещение 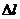численно равна площади заштрихованного треугольника, т.е. 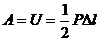, но 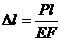, тогда .

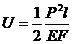Подставляя вместо внешней силы 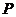, равной ей внутреннюю силу 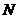получим:

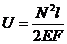, (2.9)

если 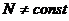, то 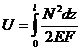. (2.9’)

Анализ напряженного состояния при растяжении (сжатии)

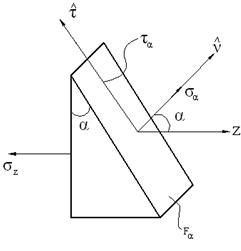
Возьмем растянутый брус (рис. 2.6,а). Из него вырежем параллелепипед с гранями 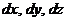. На гранях этого параллелепипеда будет действовать только нормальное напряжение — 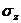. Такое напряженное состояние называется растяжением.

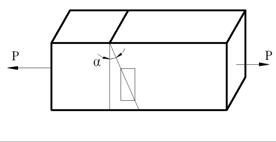
а) б)

Рис. 2.6

Рассечем параллелепипед наклонной плоскостью и рассмотрим равновесие одной из частей (рис. 2.6,б). Разложим вектор полного напряжения

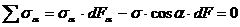
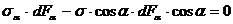
После сокращения получим 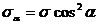. (2.10)

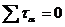
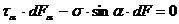, т.к.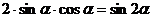

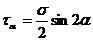. (2.11)

Из этих формул видно, что нормальные напряжения имеют максимальное значение при 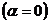, , 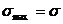а касательное напряжение в поперечных сечениях отсутствует. Касательные напряжения имеют максимальные значения при .

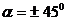Статически определимые и статически неопределимые задачи при растяжении и сжатии

Задача называется статически определимой, если все опорные реакции, а также внутренние силовые факторы в любом сечении, можно определить только с помощью уравнений статики.

Статически неопределимые называются задачи, которые нельзя решить с помощью только уравнений статики. Дополнительные уравнения составляются из рассмотрения деформаций системы.

Назовем степенью статической неопределенности разность между числом неизвестных и числом независимых уравнений статики, которые можно составить для данной задачи.

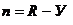. (2.12)

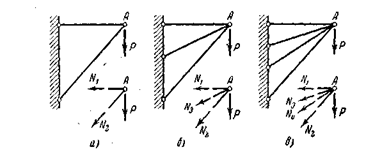
Рис. 2.7

На рис. 2.7 представлены системы: а) статически определимая, б) один раз статически неопределима 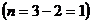, в) два раза статически неопределима .

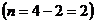Покажем другие системы (рис. 2.8, 2.9).

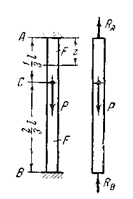
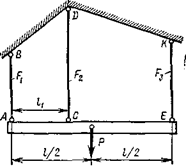
Рис. 2.8 Рис. 2.9

На данные системы наложены по одной “лишней” связи, т.е. они являются один раз статически неопределимыми.

Диаграмма растяжения

Для изучения свойств материалов под нагрузкой производят испытания образцов, изготовленных из этих материалов. Эти испытания проводят с целью определить числовые характеристики, позволяющие оценить прочность и пластичность материала. Такие характеристики называют механическими.

Важнейшие механические свойства реальных тел могут быть выявлены из опытов на растяжение — сжатие. Эти опыты проводят на специальных машинах. На рис. 2.10 приведена схема одной из испытательных машин ZD-10/90.

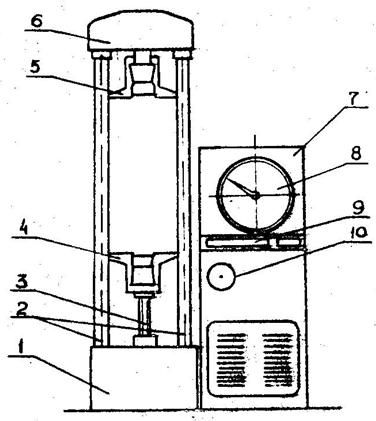
Рис. 2.10

Данная машина предназначена для проведения испытаний на растяжение, сжатие и изгиб с максимальным усилием до 100 кН. Она состоит из самой машины и пульта управления. Основные узлы: 1 — основание; 4, 5 — нижняя и верхняя траверса; 6 — поперечная траверса; 7 — пульт управления. Основание (1) выполнено в виде литой конструкции, где установлены колонны (2) и червячный привод. Приводной двигатель расположен на основании пульта управления (7), который через клиноременные шкивы передает вращение на вал червячной передачи. Червячное колесо надето на гайку ходового винта (3). Ходовой винт соединен через съемный шпиндель с нижней траверсой (4). Направление движения траверсы осуществляется по ходовым каткам. Верхняя траверса (5) закреплена на поперечной траверсе (6) и жестко соединена с датчиком измерения усилия. На верхней и нижней траверсе устанавливаются захваты для испытываемых образцов. На пульте управления (7) размещаются: стрелочный динамометр (8), панель управления, ручной привод (10), регистрирующее устройство (9). Общий вид машины представлен на рис. 2.11.

Рис. 2.11

Испытания проводят на стандартных образцах круглой или плоской формы (рис. 2.12,а, б).

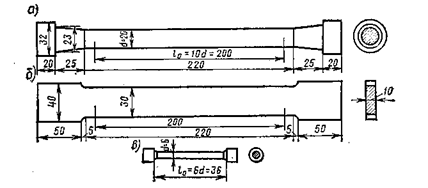
Рис. 2.12

На рис. 2.13 показана типичная для углеродистой стали диаграмма растяжения, полученная в результате испытания.

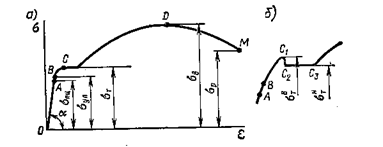
Рис. 2.13

Напряжения вычисляем по формуле 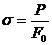, 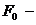первоначальная площадь.

Деформации вычисляем по формуле:

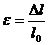, где 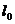— первоначальная длина образца.

На участке справедлив закон Гука 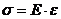, т.е. напряжения, растут прямо пропорционально деформации. Пределом пропорциональности 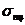называют наибольшее напряжение, при котором справедлив закон Гука. (Для стали Ст3 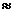21 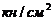). Угол наклона этой прямой можно определить как .

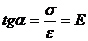Выше точки 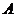диаграмма искривлена и нарушается закон Гука. Очень близко к точке 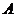, на криволинейном участке, можно отметить точку 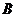, соответствующую пределу упругости. Пределом упругости 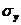называют максимальное напряжение, при котором в материале не возникает остаточной деформации, определяемой при разгрузке. По Госту условным пределом упругости называют напряжение, при котором остаточная деформация достигает 0,05 % и обозначают 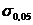. Точка 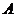находится вблизи точки 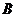поэтому их часто считают совпадающими.

Начиная с некоторой точки 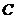диаграмма имеет почти горизонтальный участок, на нем деформации растут без увеличения нагрузки 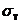. Пределом текучести называется напряжение при котором деформации растут без увеличения напряжения. Для стали Ст3

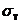=24 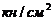. Площадка текучести наблюдается только для малоуглеродистых сталей. Большинство материалов не имеет площадки текучести.

После площадки текучести нагрузка на образец, а, следовательно, напряжения, вновь начинают расти. Происходит самоупрочение материала до точки 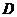. Пределом прочности (временным сопротивлением) 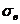называют отношение наибольшей нагрузки, выдерживаемой образцом, к первоначальной площади поперечного сечения. Предел прочности является некоторой условной характеристикой, т.к. она не является напряжением, при котором материал разрушается, т.к. площадь поперечного сечения при разрушении значительно меньше (для стали Ст3 ).

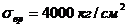До точки 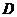деформация стержня является равномерной. После точки 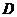она концентрируется в одном месте (наиболее слабом) начинает образовываться шейка — местное сужение образца (рис. 2.14,а). Наконец в точке 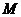наступает разрыв образца. Этой точке соответствует 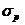— условное напряжение при разрыве.

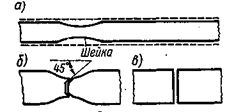
Рис. 2.14

При разрыве на одной части образца виден конус, а на другой кратер (рис. 2.14,б): угол с осью 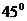. Такая форма разрушения образцов из малоуглеродистой стали, показывает, что разрушение связано со сдвигом по площадкам, наклоненным под 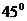к оси стержня, где касательные напряжений будут наибольшими. Такой тип разрушения пластичных материалов называют разрушение путем сдвига.

Для сравнения диаграмм растяжения на рис. 2.15 представлены диаграммы некоторых других материалов.

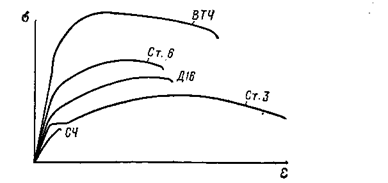
Рис. 2.15

Сталь Ст.6 по сравнению со сталью Ст.3 обладает значительно более высокими характеристиками прочности. Площадка текучести у высокопрочных сталей, как правило, отсутствует или имеет очень малую протяженность. Высокими механическими свойствами обладает титановый сплав ВТ4. Диаграмма растяжения чугуна (С4) вообще не имеет прямого участка, она искривляется уже в самом начале. Чугун, строго говоря, вообще не подчиняется закону Гука.

Диаграмма сжатия

Для изучения “поведения” материалов при сжатии строятся диаграммы сжатия. Испытания металлов на сжатие производятся на образцах в виде цилиндров, высота которых равна их диаметру (обычно d=h=20 мм). Для других материалов (дерево, цемент, бетон) применяют образцы в виде кубиков.

Рассмотрим диаграммы сжатия, стали и чугуна. Для наглядности изобразим их на одном рисунке с диаграммами растяжения (рис. 2.16).

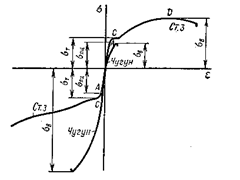
Рис. 2.16

При испытании Ст3 на сжатие σ_нц , σ_у, σ_т примерно такие же как и их растяжение. Затем образец в силу наличия трения по торцам приобретает форму бочонка и дальше расплющивается (рис. 2.17), но разрушить его не удается, поэтому предел прочности установить нельзя. Условно принимают предел прочности при сжатии такой же, как и растяжения.

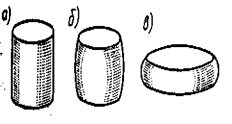
Рис. 2.17

Диаграмма сжатия чугуна по форме напоминает диаграмму растяжения. Она криволинейна с самого начала. Однако предел прочности при сжатии чугуна примерно в 4-5 раз выше предела прочности при растяжении. При испытании чугунного образца (рис. 2.18, а) продольные деформации его незначительны. Образец несколько выпучивается в средней части, принимая слегка бочкообразную форму, после чего в нем появляются трещины под углом примерно 45⁰ к оси по площадкам с наибольшими касательными напряжениями (рис. 2.18, б).

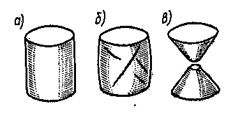
Рис. 2.18

В это время нагрузка резко падает и диаграмма обрывается. В момент разрушения боковые части образца отделяются и он принимает вид двух усеченных конусов (рис. 2.18, в).