Коррелированность и зависимость составляющих X,Y двумерной СВ X,Y

Две СВ X,Y наз-т коррелированными,если их корреляционный момент (или,что то же ,коэффициент корреляции) отличен от нуля,X,Y наз-т некоррелированными величинами,если их корреляционный момент равен нулю

Две коррелированные величины также и зависимы.Действительно,допустим противное,мы должны заключит,что µxy = 0, а это противоречит условию,так как для коррелированных величин µxy не равно 0.Обратное прелположение не всегда имеет место,т.е. если две величины зависимы,то они могут быть как коррелированными,так и некоррелированными. Другими словами ,коррелированный момент двух зависимых величин может быть не равен нулю,но может и равняться нулю.

2.29. Лин.регресссияПрямые среднеквадорат. Регрессии.Коэффиц. регрессии.Остаточная регрессия.Центр совместного распределения.

Рассмотрим двумерную величину СВ (Х,У),где Х и У-зависимые СВ будем полагать 1 из них как ф-ю другой.Уz g(x)=kX+b, где к и b-подлежащие определению коэф-ты.Для их определ. Применяют метод наименьших квадратов,закл. В том, что мат. Ожидание М(У-g(х))² приняло как можно меньше знач.мод наз. Среднеквадр. Регрессией величины У относит. Х.Исследовав ф-ю М((У-g(х))²)=М((У-кХ-b²))получим, что наимен. Ее знач. =σх²(1-τ_ху²) если k= τ_ху и b=М(У)- τ_ху М(Х). Величина σ_у²(1-τ²_ху)наз. Остаточной дисперсией У относит. Х,она характеризует ошибку,кот. Достигается при замене У на g(х).Если τ_ху = 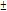1,то остаточная дисперсия =0. K - коэф-т регрессииУ относит. Х, а прямую заданную уравнением у= τ_ху (x-m_х)+m_уназ. Прямой среднеквадрат. Регрессии У относит.Х. Аналогично можно получить прямую среднеквадрат. Регрессии Х относит. У: Х= τ_ху (у-m_у)+m_x. Коэф-т регрессии Х относит. У - τ_{ху .} Остаточная дисперсия Х относит. У. σ²_х(1- τ_ху²). Если τ_ху= 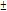1, то обе прямые регрессии совпадают. В любом случае прямые проходят через точку с координатами (m_x,m_y),кот. Наз. Центром совместного распределения Х и У).

2.30. Лин. Корреляц. Распредел. Двумерной случ. Величины.

Если обе ф-ии М(У/Х=х) и М(Х/У-у) линейны, кот. Говорят, что СВ Х и У связаны лин. Коррел. Зависимостью.Графики лин. Ф-й регрессии – прямые линии,совпадающие с прямыми среднеквадрат. Регрессии. ТЕОРЕМА. Если(Х,У)- двумерная СВ,распредел. По норм. Закону, тоХ и У связаны лин. Корреляц. Зависимостью. Док-во. F(х,у)- плотность распредел. Двумерной СВ (Х,У), f₁(х) – плотность вероятности .ψ (у/х)= 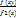= 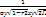. Как видно,это норм. Распредел. Мат. Ожидание равно: М(У/Х=х)=а₂+ τ_ху (х-а₁). D(У/Х=х)=/у²(1-r²ху).

3.1 Задачи мат. статистики: - указать способы сбора и группировки статистических сведений. – разработать методы анализа статистических данных, в зависимости от целей исследования.

Выборочный метод - статистический метод исследования общих свойств совокупности каких-либо объектов на основе изучения свойств лишь части этих объектов, взятых на выборку.

Генеральная совокупность – совокупность объектов, из которых производится выборка.

Выборочная совокупность – совокупность случайно отобранных объектов.

Повторной называют выборку, при которой отобранный объект возвращается в генеральную совокупность.

Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.

Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот (числа наблюдений называют частотами, а их отношение к объему выборки n_i/n=w_i – относительными частотами).

Эмпирической функцией распределения (функцией распределения выборки) называют функцию F*(x), определяющая для каждого значения х относительную частоту события Х<x. F*(x)=n_x/n, где n_x - число вариант, меньших х, n – объем выборки, Х – статистическое распределение частот количественного признака.

Полигоном частот называют ломанную, отрезки которой соединяют точки (х_1, n₁), (х_2, n₂),…, (х_k, n_k). Для построения полигона частот на оси абсцисс откладывают варианты х_i, а на оси ординат – соответствующие им частоты n_i. Точки (х_i, n_i) соединяют отрезками прямых и получают полигон частот.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению n_i/h (плотность частоты). Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии n_i/h.

3.2 Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.

Несмещенной называют статистическую ошибку Q^*, математическое ожидание которой равно оцениваемому параметру Q при любом объеме выборки, т.е. М (Q^*)=Q. Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.

Эффективной называют статистическую оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию. При рассмотрении выборок большого объема (n велико!) к статистическим оценкам предъявляется требование состоятельности.

Состоятельной называют статистическую оценку, которая при n → ∞ стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при n → ∞ стремится к нулю, то такая оценка оказывается и состоятельной.

3.3 Генеральной средней ¯Х_г называют среднее арифметическое значении признака генер. совокупности. Если все значения Х₁, Х₂,…, Х_n признака генер. совокупности объема N различны, то ¯Х_г =( Х₁+ Х₂+,…, Х_n)/N. Если значения признака Х₁, Х₂,…, Х_К имеют соответственно частоты N_1, N_{2, ….}N_{к ,} причем N₁+ N₂+_{, ….}N_к= N, то ¯Х_г =(x₁N₁+x₂N₂+…+x_kN_k)/N. Выборочной средней ¯Х_в называют среднее арифметическое значение признака выборочной совокупности. . Если все значения Х₁, Х₂,…, Х_n признака выборки объема n различны, то ¯Х_в =( Х₁+ Х₂+,…, Х_n)/n. Если значения признака Х₁, Х₂,…, Х_К имеют соответственно частоты n_1, n_{2, ….}n_{к ,} причем n₁+ n₂+_{, ….}n_к= n, то ¯Х_в =(x₁n₁+x₂n₂+…+x_kn_k)/n. Групповой средней называют среднее арифметическое значений признака, принадлежащее к группе. Общей средней ¯х назыавют среднее арифметическое значений признака, принадлежащих всей совокупности. Модой М₀ называют варианту, которая имеет наибольшую частоту. Медианой m_е (m_e= (x_k+x_k+1)/2) называют варианту, которая делит вариационный ряд на две части, равные по числу вариант. Размахом варьирования R называют разность между наибольшей и наименьшими вариантами (R= x_max-x_min). Средним абсолютным отклонением Ѳ называют среднее арифметическое абсолютных отклонений (Ѳ=(∑n_i|x_i-¯Х_в |)/∑n_i). Коэффициентом вариации V называют выражении в процентах отношение выборочного среднего квадратического отклонения к выборочной средней (V=σ_в/¯Х_в *100%).

3.5. Генеральной дисперсией D_г наз. среднее арифметич. квадратов отклонений знач. признака генер. совок-ти от их сред. знач. 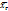. Если все значения х₁, х₂,…,х_n признака генер. совок-ти объема N различны, то 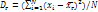_. Если все значения х₁, х₂,…,х_к имеют соответственно частоты N_!, N₂,…, N_K, причем N₁+N₂+…+N_k=N, то 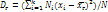, т.е. генер. дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответств. частотам. Выборочной дисперсией D_в наз. среднее арифметич. квадратов отклонений наблюдаем. значений признака от их сред. значения 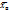. . Если все значения х₁, х₂,…,х_n признака выборки объема n различны, то 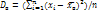_. Если все значения х₁, х₂,…,х_к имеют соответственно частоты n_!, n₂,…, n_K, причем n₁+n₂+…+n_k=n, то 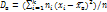, т.е. выборочная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответств. частотам. Групповой средней наз. среднее арифметич. значений признака, принадлежащих группе. Общей средней наз. среднее арифметич. значений признака, принадлежащих всей совокупности. Общая средняя равна средней арифметич. групп. средних, взвешенной по объемам групп. Модой М_о наз. варианту, кот. имеет наиб частоту. Медианой m_е наз. варианту, кот. делит вариац. ряд на две части, равные по числу вариант. Размахом варьирования R наз. разность между наибольшей и наименьшей вариантами: 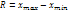. Средним абсолютным отклонением наз. сред. арифметич. абсолютных отклонений: 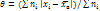. Коэффициентом вариации V наз. выраженное в процентах отношение выборочного среднего квадрат. откл. к выбороч. средней: 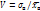*100% .

3.6 Групповой дисперсией наз. дисперсию значений признак, принадлжежащих группе, относительно групповой средней: 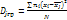, где n_j-частота значения х_i; j – номер группы; 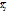-групповая средняя группы j; N_j= 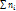-объем группы j. Внутригрупповой дисперсией наз. среднюю арифм. дисперсий, взвешенную по объемам групп: 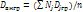, N_j-объем группы j; 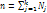-объем всей совокупности. Межгрупповой дисперсией наз. дисперсию групповых средних относительно общей средней: 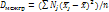, 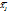– групповая средняя группы j; N_j-объем группы j; -общая средняя; 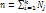-объем всей совокупности. Общей дисперсией наз. дисперсию значений признака всей совок-ти относительно общей средней: 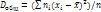. Теорема о сложении дисперсий: если совок-ть состоит из нескольких групп, то общая дисперсия равна сумме внутригру. и межгруп. дисперсий: D_общ=D_внгр+D_межгр.