К.п.д. и коэффициент мощности регулируемого электропривода.

Все способы регулирования скорости электроприводов можно разделить на две группы. 1ая- при которых скорость идеального холостого хода w₀ электродвигателя остается постоянной. 2ая - скорость идеального холостого хода w₀ электродвигателя изменяется с помощью управляющего воздействия. Для выявления особенностей к.п.д. регулируемого электропривода при w₀=const рассмотрим реостатное регулирование скорости ДПТ НВ. Запишем к.п.д ДПТ НВ в виде 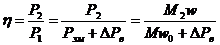,(6.70)

Для двигательного режима момент на валу М₂ можно выразить через электромагнитный момент М и потерю момента: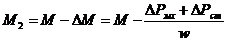

Для двигателей постоянного тока при регулировании скорости принимают

,

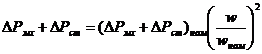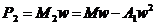, (6.73) где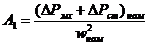

При номинальном магнитном потоке 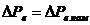.Разделим числитель и знаменатель на величину Р_НОМ=М_НОМω_НОМ, в результате получим 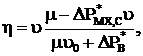(6.77)

где 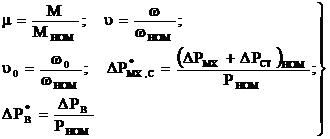(6.78)

Если определить диапазон регулирования скорости: 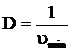(6.79)

Для электродвигателей нормального исполнения при μ=1 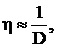(6.81)

А теперь посмотрим, как будет изменятся к.п.д. асинхронного двигателя при ω₀=const и изменении угловой скорости ротора ω за счет скольжения s. K.п.д. асинхронного двигателя: 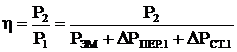(6.82)

При понижении скорости ротора с увеличением скольжения механические потери уменьшаются, а потери в стали ротора возрастают. Их сумму примерно можно считать постоянной, тогда 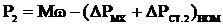(6.83)

Получаем к.п.д.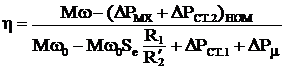

Для линейной части ест механической характеристики АД справедливо соотношение ,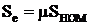

Разделив числитель и знаменатель (6.84) на Р_НОМ=ω_НОММ_НОМ и принимая во внимание (6.85), найдем 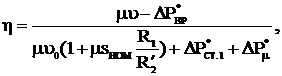(6.86)

где 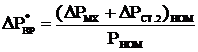(6.87) 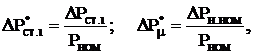(6.88)

Рассмотрим к.п.д. и коэффициент мощности регулируемого электропривода при ω₀=var.

Если регулирование скорости ДПТ НВ осуществляется изменением подводимого напряжения при постоянном токе возбуждения, равном номинальному, то постоянные потери мощности в регулируемом ДПТ НВ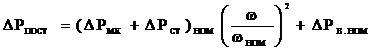

Для частотного регулирования АД по закону Ф=const имеем 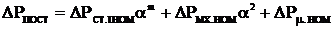(6.90) где m=1,3÷1,5; .

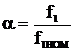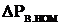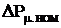Если не учитывать постоянные величины потерь на создание магнитного поля ( и ), то постоянные потери ДПТ НВ и АД будут примерно пропорциональны квадрату относительной скорости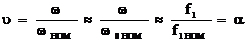

примем, что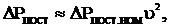

Введем коэффициент загрузки двигателя моментом 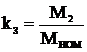(6.93)

С учетом этих обозначений определяем мощность на валу электродвигателя

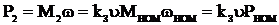и суммарные потери мощности

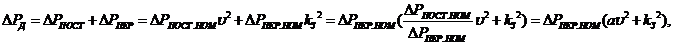
где 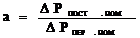К.п.д. регулируемого электродвигателя определяется отношением мощности на валу к потребляемой мощности: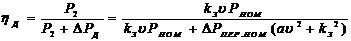

к.п.д. 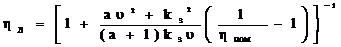является функцией двух независимых переменных ( 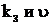), где в качестве парам выступают ном к.п.д. 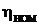и коэффициент потерь а.

Решив уравнение 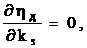найдем оптимальный коэф загрузки регулируемого эд

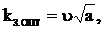(6.100) который соответствует равенству постоянных и переменных потерь.

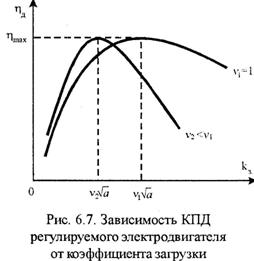Коэффициент полезного действия регулируемого электропривода включает произведение трех к.п.д.: управляемого преобразователя, электродвигателя и передаточного механизма, т.е.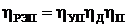

Коэффициент мощности k_M определяется выражением

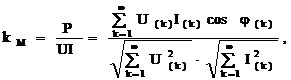где Р – активная

,

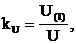
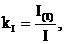
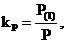
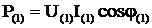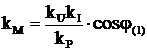
16. ПОТЕРИ ЭНЕРГИИ В ПЕРЕХОДНЫХ ПРОЦЕССАХ ЭЛЕКТРОПРИВОДА(ω₀=CONST) .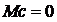

Потери энергии в переходных процессах электропривода зависят от системы электропривода и способа формирования переходного процесса и в общем случае определяются выражением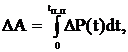

где ΔP(t) – суммарные потери мощности в данный момент времени переходного процесса, t_П.П. – время переходного процесса.

Главнейшим фактором, определяющим потери энергии в переходном процессе, является характер изменения скорости ω₀ идеального холостого хода.

В электроприводах с ω₀=const управляющее воздействие изменяется скачком. Потери мощности в якорной цепи ДПТ НВ и в роторной цепи АД: ΔР= Р_ЭМ – Р_МХ=М(ω₀–ω)

Соответственно потери энергии будут равны разности электромагнитной А₁ и полной механической А₂ энергий электропривода: ΔА= А₁ – А₂

где 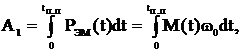(6.123)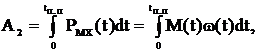

Pассмотрим частный случай при М_С=0: М=М_ДИН=J ,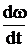

что при подстановке в (6.123) и (6.124) приводим к результату 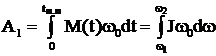(6.126) 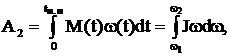(6.127)

где ω₁ и ω₂ – угловые скорости электродвигателя в начале и в конце переходного процесса, J – суммарный момент электропривода.Произведение Jω есть момент количества движения и имеет размерность H·м·с·рад.

Потери энергии в электроприводе можно записать в виде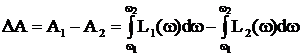

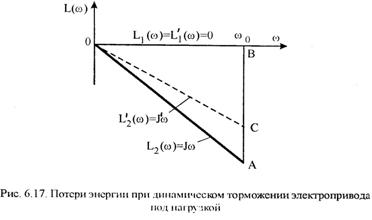
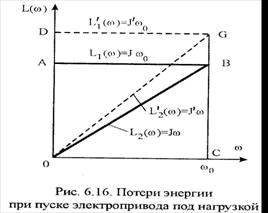
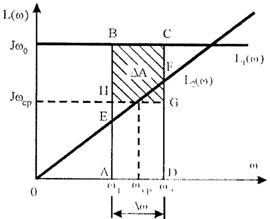
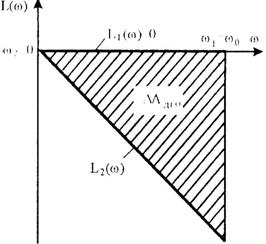
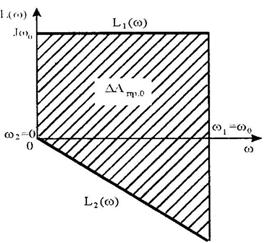
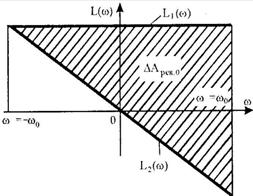
Где L₁(ω)=Jω₀, (6.132) L₂(ω)=Jω,

Соотношение (6.131) можно представить графически

Возьмем интегралы:

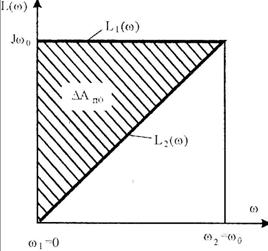
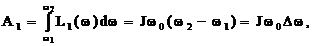(6.134) 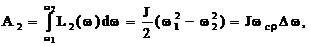(6.135) где Δω = ω₂ – ω₁ ω_сρ= ½(ω₂ + ω₁) В результате можем записать общую формулу для определения потерь энергии в якорной (роторной) цепи электропривода за время переходного процесса при ω₀=const и М_С=0: ΔА₀ = JΔω(ω₀ – ω_сρ) при ω₀=const и М_С=0.

Пуск вхолостую: ω₁=0; ω₂=ω₀; ω_сρ= ½(ω₂ + ω₁)= ½ ω₀; Δω = ω₂ – ω₁= ω₀. Находим А₁=Jω₀Δω=J 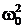; А₂=Jω_сρΔω= ½ J 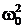; ΔА_по=А₁ – А₂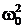=J – ½ J = .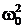

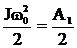Динамическое торможение вхолостую:

ω₁=ω₀; ω₂=0; ω_сρ= 0,5(ω₂ + ω₁)= 0,5ω₀; Δω = ω₂ – ω₁= –ω₀.

Так как при динамическом торможении якорь электродвигателя отключен от силовой цепи, то L₁(ω)=0; А₁=0.

Полная механическая мощность: А₂=Jω_сρΔω= –½ J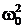

и потери энергии ΔА_дто=А₁ – А₂=0–(-½ J )= .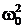

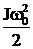Следовательно, при динамическом торможении вхолостую потери энергии равны запасу кинетической энергии электропривода, так как при динамическом торможении теряется вся накопленная механическая энергия (рис.6.13). поэтому при динамическом торможении вхолостую потери энергии равны потерям энергии при пуске вхолостую.

Торможение противовключением в холостую:

ω₁=ω₀; ω₂=0; ω₀<0; ω_сρ= 0,5(ω₂ + ω₁)= 0,5ω₀; Δω = ω₂ – ω₁=0–ω₀= –ω₀.

Вычисляем: А₁=Jω₀Δω=J(-ω₀)(-ω₀)=J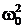; А₂=Jω_сρΔω= ½ J 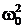(-ω₀)= –½J 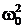; ΔА_пр.о=А₁ – А₂=J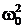–(–½ J )=

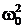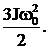
Реверс вхолостую:

ω₁=ω₀; ω₂= –ω₀; ω₀<0; ω_сρ= 0,5(ω₂ + ω₁)= 0; Δω = ω₂ – ω₁= –2ω₀.

Определяем: А₁=Jω₀Δω=J(-ω₀)(-2ω₀)=2J ;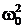

А₂=Jω_сρΔω= J·0·(-2ω₀)=0;

ΔА_рев.о=А₁– А₂=2J =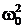

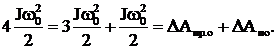
Полученные соотношения соответствуют потерям энергии в якоре ДПТ НВ и в роторе АД. Потери энергии ΔА₁ в статоре АД определяются через потери ΔА₂ в роторе таким образом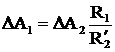

Теперь можно записать суммарные потери энергии в асинхронном двигателе в переходном процессе электропривода вхолостую: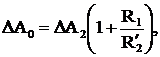

Где 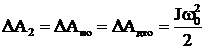(6.141) 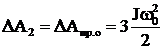(6.142)

17 ПОТЕРИ ЭНЕРГИИ В ПЕРЕХОДНЫХ ПРОЦЕССАХ ЭЛЕКТРОПРИВОДА(ω₀=const) .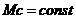

Потери энергии в переходных процессах электропривода зависят от системы электропривода и способа формирования переходного процесса :

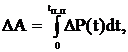
Главнейшим фактором, определяющим потери энергии в переходном процессе, является характер изменения скорости ω₀ идеального холостого хода.

Потери мощности в якорной цепи ДПТ НВ и в роторной цепи АД:

ΔР= Р_ЭМ – Р_МХ=М(ω₀–ω)

Соответственно потери энергии будут равны разности электромагнитной А₁ и полной механической А₂ энергий электропривода:

ΔА= А₁ – А₂

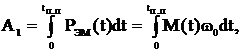
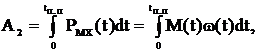
Примем допущение, что в переходном процессе электромагнитный момент эд равен его среднему значению М_СР.

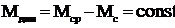
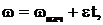
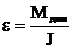М(t)=М_ср= М_с+ М_дин

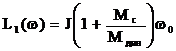
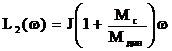
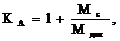
Пусть 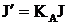тогда , ,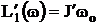

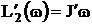Потери энергии в переходном процессе при допущении 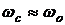будут равны:

,
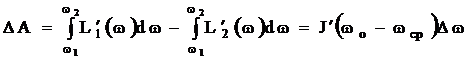