Кпд и коэффициент мощности нерегулируемого электропривода

Сначала рассмотрим к.п.д. и коэффициент мощности нерегулируемого электропривода. К.п.д. нерегулируемого электропривода представляет собой отношение мощности Р_р.0 на рабочем органе машины к мощности Р₁, потребляемой из сети:

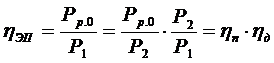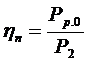где (6.54)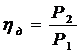

h_n, h_д – соответственно к.п.д. механической передачи и к.п.д. электродвигателя,

Р₂ – мощность на валу электродвигателя.

Если принять для рабочего участка естественной механической характеристики, где скорость незначительно изменяется, коэффициент загрузки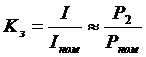

то, используя (6.17), к.п.д. электродвигателя можно записать таким образом:

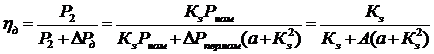, где ,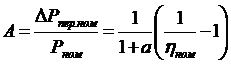

Подставив выражение коэффициента А через номинальный к.п.д. h_ном и коэффициент потерь а в (6.57), получим окончательное выражение для к.п.д. нерегулируемого электродвигателя 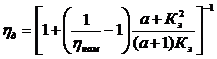(6.59)

Из (6.59) видно, что к.п.д. нерегулируемого электродвигателя является сложной функцией коэффициента загрузки К_з. Значение оптимального коэффициента загрузки, при котором к.п.д. достигает максимальной величины, определяем из решения уравнения

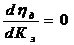, (6.60) т.е. 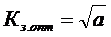Подставив (6.61) в (6.59), найдем максимум к.п.д. 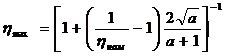Определим переменные потери мощности при оптимальном коэффициенте загрузки:

,

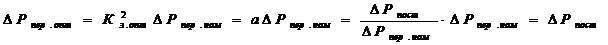следовательно, максимум к.п.д. достигается, когда постоянные потери становятся равными переменным.

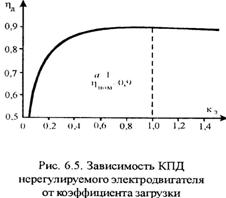
При а<1 максимум к.п.д. имеет место при нагрузке, меньше номинальной, а при а>1 – больше номинальной. Если а=1 то максимум к.п.д. соответствует номинальному к.п.д. (рис.6.5).

Обычно электродвигатели длительного режима (s1) проектируют таким образом, чтобы максимум к.п.д. был при коэффициенте загрузки К_з=0,75. этим самым учитывается возможность и наибольшая вероятность работы электродвигателя в режиме s1 с небольшой недогрузкой. С ростом мощности к.п.д. электродвигателя возрастает.

Для электрических двигателей переменного тока важным энергетическим показателем является коэффициент мощности, который при синусоидальных токах и напряжения cosj: ,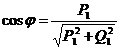

где Р₁ – потребляемая электродвигателем активная мощность.

Q₁ – “потребляемая” реактивная мощность из сети.

Для трехфазного асинхронного двигателя 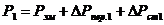,(6.65) 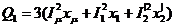, (6.66)

где 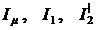– намагничивающий ток, ток статора и приведенный ток ротора,

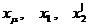– индуктивные сопротивления намагничивающего контура, рассеяния статора и ротора (приведенное).

Реактивную мощность Q₁ можно выразить через активную Р1, используя треугольник мощностей: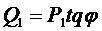

Для большинства асинхронных двигателей cosj_ном»0,8¸0,9, что дает

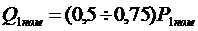
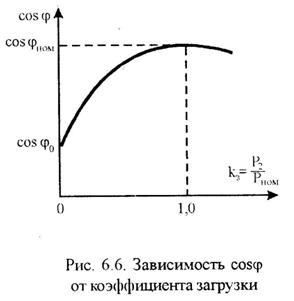Характер зависимости cosj от коэффициента загрузки показан на рис.6.6.

Поскольку потери мощности в активных сопротивлениях R источника, линии и приемника определяются полным током I, то при заданной активной мощности Р=Р_ср эти потери будут равны

,

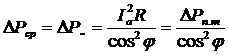где I_а – активная составляющая полного тока I,

DР_n.т – потери при передачи мощности Р постоянным током (I_а=I_n.т).

выражение (6.69) показывает, что cosj является энергетической характеристикой, определяющей экономичность потребления активной энергии на переменном токе, с увеличением cosj уменьшаются потери при передаче заданной активной мощности от источника приемнику электроэнергии.

В синхронном двигателе cosj зависит от нагрузки так же, как и в асинхронном.