Сложение вращений вокруг параллельных осей
Рассмотрим случай, когда относительное движение тела является вращением
с угловой скоростью 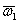 вокруг оси
вокруг оси 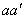 , закрепленной на кривошипе
, закрепленной на кривошипе 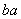 (рис.1а), а переносное – вращением кривошипа
(рис.1а), а переносное – вращением кривошипа 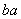 вокруг оси
вокруг оси 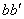 , параллельной
, параллельной 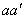 , с угловой скоростью
, с угловой скоростью 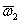 . Тогда движение тела будет плоскопараллельным по отношению к плоскости, перпендикулярной к осям.
. Тогда движение тела будет плоскопараллельным по отношению к плоскости, перпендикулярной к осям.
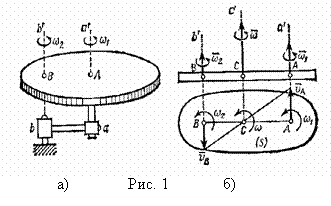
Примем, что вращения направлены в одну сторону. Изобразим сечение 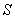 тела плоскостью, перпендикулярной осям (рис. 1 б). Следы осей в сечении
тела плоскостью, перпендикулярной осям (рис. 1 б). Следы осей в сечении 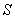 обозначим буквами
обозначим буквами 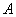 и
и 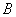 . Тогда
. Тогда 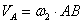 и
и 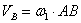 . При этом векторы
. При этом векторы 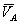 и
и 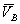 параллельны друг другу, перпендикулярны
параллельны друг другу, перпендикулярны 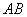 и направлены в разные стороны. Тогда точка
и направлены в разные стороны. Тогда точка 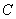 является мгновенным центром скоростей
является мгновенным центром скоростей 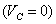 , а следовательно, ось
, а следовательно, ось 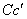 , параллельная осям
, параллельная осям 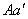 и
и 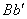 , является мгновенной осью вращения. Для определения угловой скорости
, является мгновенной осью вращения. Для определения угловой скорости 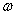 абсолютного вращения тела вокруг оси
абсолютного вращения тела вокруг оси 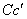 и положения самой оси, т.е. точки
и положения самой оси, т.е. точки 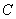 , воспользуемся свойством мгновенного центра скоростей
, воспользуемся свойством мгновенного центра скоростей
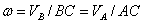 ,
,
откуда
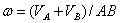 .
.
Подставив в эти равенства значения 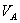 и
и 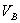 , окончательно получим
, окончательно получим
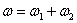 | (1) | |
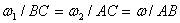 | (2) |
Итак, при сложении двух направленных в одну сторону вращений вокруг параллельных осей результирующее движение тела будет мгновенным вращением с абсолютной скоростью 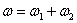 вокруг мгновенной оси, параллельной данным, положение которой определяется пропорциями (2).
вокруг мгновенной оси, параллельной данным, положение которой определяется пропорциями (2).
С течением времени мгновенная ось вращения  меняет свое положение, описывая цилиндрическую поверхность.
меняет свое положение, описывая цилиндрическую поверхность.
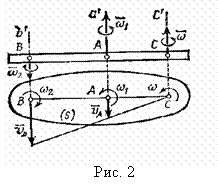
Рассмотрим теперь случай, когда вращения направлены в разные стороны (рис.2).
Допустим, что 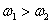 . Тогда, рассуждая, как в предыдущем случае, для угловой скорости
. Тогда, рассуждая, как в предыдущем случае, для угловой скорости 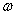 абсолютного движения тела вокруг оси
абсолютного движения тела вокруг оси 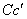 и положения самой оси, получим
и положения самой оси, получим
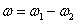 | (3) | |
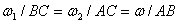 | (4) |
Таким образом, при сложении двух направленных в разные стороны вращений вокруг параллельных осей, результирующее движение тела будет мгновенным вращением с абсолютной угловой скоростью 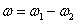 вокруг мгновенной оси, положение которой определяется пропорциями (4).
вокруг мгновенной оси, положение которой определяется пропорциями (4).
Заметим, что в этом случае точка 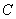 делит расстояние между параллельными осями внешним образом.
делит расстояние между параллельными осями внешним образом.
Рассмотрим частный случай, когда вращения вокруг параллельных осей направлены в разные стороны, но по модулю 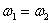 (рис.3).
(рис.3).
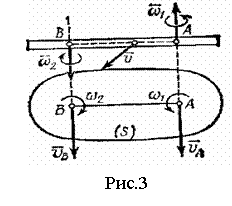
Такая совокупность вращений называется парой вращений, а векторы 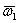 и
и 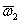 образуют пару угловых скоростей. В этом случае получим
образуют пару угловых скоростей. В этом случае получим 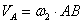 и
и 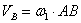 , то есть
, то есть 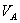 =
= 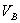 . Тогда мгновенный центр скоростей находится в бесконечности и все точки тела в данный момент времени имеют одинаковые скорости
. Тогда мгновенный центр скоростей находится в бесконечности и все точки тела в данный момент времени имеют одинаковые скорости 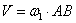 .
.
Следовательно, результирующее движение тела будет поступательным (или мгновенно поступательным) движением со скоростью, численно равной 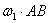 и направленной перпендикулярно плоскости , проходящей через векторы
и направленной перпендикулярно плоскости , проходящей через векторы 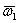 и
и 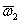 . Таким образом, пара вращений эквивалентна мгновенно поступательному движению со скоростью
. Таким образом, пара вращений эквивалентна мгновенно поступательному движению со скоростью 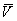 , равной моменту пары угловых скоростей этих вращений.
, равной моменту пары угловых скоростей этих вращений.
Примером пары угловых скоростей является движение велосипедной педали 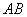 относительно рамы велосипеда (рис.4).
относительно рамы велосипеда (рис.4).
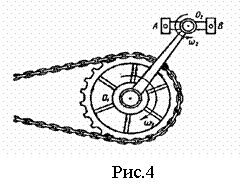
Это движение представляет собой совокупность переносного вращения вместе с кривошипом 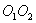 вокруг оси
вокруг оси 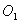 и относительного вращения педали по отношению к кривошипу вокруг оси
и относительного вращения педали по отношению к кривошипу вокруг оси 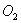 . Педаль
. Педаль 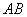 за все время движения остается параллельной своему первоначальному положению, т.е. совершает поступательное движение.
за все время движения остается параллельной своему первоначальному положению, т.е. совершает поступательное движение.
Рассмотрим несколько примеров.
Пример 1. Кривошип 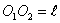 вращается вокруг оси
вращается вокруг оси 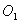 по часовой стрелке с угловой скоростью
по часовой стрелке с угловой скоростью 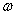 , а диск радиуса
, а диск радиуса 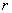 вращается вокруг оси
вращается вокруг оси 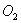 по часовой стрелке с той же угловой скоростью
по часовой стрелке с той же угловой скоростью 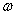 относительно кривошипа. Найти величину и направление абсолютных скоростей точек
относительно кривошипа. Найти величину и направление абсолютных скоростей точек 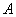 и
и 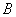 (рис.5).
(рис.5).
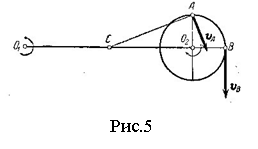
Решение. Так как угловые скорости переносного и относительного вращений равны по модулю и направлены в одну сторону, то мгновенный центр вращений 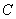 диска лежит посредине между
диска лежит посредине между 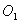 и
и 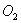 , т.е.
, т.е. 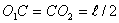 . Модуль абсолютной угловой скорости
. Модуль абсолютной угловой скорости 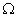 вращения диска вокруг точки
вращения диска вокруг точки 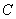 равен
равен 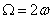 . Отсюда находим:
. Отсюда находим:
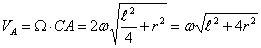 ,
, 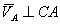 ,
,
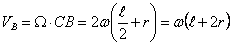 ,
, 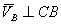 .
.
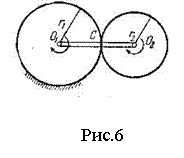
Пример 2. Кривошип 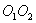 вращается вокруг оси
вращается вокруг оси 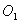 с угловой скоростью
с угловой скоростью 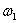 . На палец
. На палец 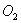 кривошипа свободно насажена шестерня радиуса
кривошипа свободно насажена шестерня радиуса 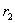 , сцепленная с неподвижным зубчатым колесом радиуса
, сцепленная с неподвижным зубчатым колесом радиуса 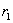 . Найти абсолютную угловую скорость
. Найти абсолютную угловую скорость 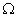 шестерни и ее угловую скорость
шестерни и ее угловую скорость 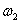 относительно кривошипа (рис.6).
относительно кривошипа (рис.6).
Решение. Так как шестерня сцеплена с неподвижным колесом, то абсолютная скорость точки 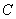 зацепления шестерни с этим колесом равна нулю, т.е. точка
зацепления шестерни с этим колесом равна нулю, т.е. точка 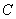 является для шестерни мгновенным центром вращения. Отсюда
является для шестерни мгновенным центром вращения. Отсюда 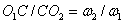 или
или 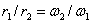 ,
,
откуда
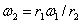 .
.
Заметим, что направление вращения шестерни совпадает с направлением вращения кривошипа.
Тогда абсолютную угловую скорость шестерни находим из равенства
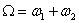
или
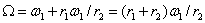 .
.
