Скорость и ускорение точки вращающегося тела

Следовательно, линейная скорость любой точки вращающегося тела равна произведению угловой скорости на расстояние от данной точки до оси вращения. Направлена эта скорость всегда по касательной к окружности, которую описывает данная точка при своем движении.

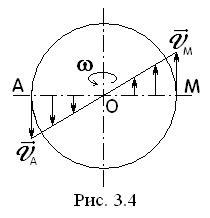В каждый данный момент времени угловые скорости точек вращающегося тела равны. Поэтому линейные скорости точек тела пропорциональны их расстоянию до оси (рис.3.4), т.е. скорость изменяется полинейному закону.

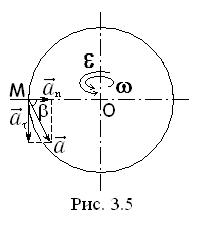Так как точки тела совершают криволинейное движение (траектории точек - окружности), то полное ускорение слагается из нормального и касательного ускорений 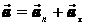, которыеопределяются ,

,

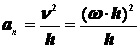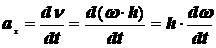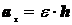(3.14)

Таким образом полное ускорение точки будет 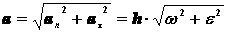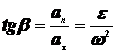(3.15)Из формул (3.15) следует, что полное ускорение точки вращающегося тела пропорционально ее расстоянию до оси вращения.

При вращательном движении тела вокруг оси нормальное ускорение 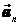называют еще центростремительным 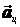(вектор направлен по радиусу к центру кривизны), касательное ускорение 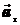называют и иначе – вращательным ускорением 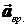(вектор ускорения направлен по касательной).

47.Скорость и ускорение точки при векторном способе заданиядвижения

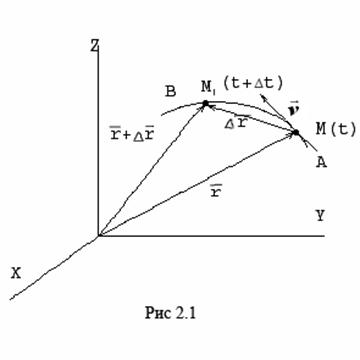Скорость точки – это величина, характеризующая как быстро и в каком направлении меняется положение точки в пространстве. Поскольку она определяет направление перемещения точки, скорость является величиной векторной. Пусть за время Δt радиус-вектор точки М изменился на величину Δ 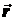.Тогда средней скоростью называется векторная величина 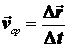(2.1)

Этот вектор направлен так же, как и 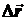. Предельное значение 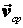, при стремящемся к нулю 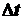, определит мгновенное значение скорости в данный момент времени

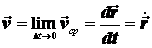(2.2)

При стремлении 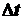к нулю хорда ММ₁, а значит и вектор 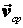поворачивается вокруг точки М, приближаясь к касательной к траектории в точке М и в пределе, совпадая с ней. Поэтому вектор 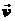направлен по касательной к траектории точки в сторону движения.

В общем случае криволинейного движения вектор скорости изменяется по величине и направлению в функции времени. Следовательно, за время 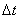вектор 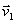можно представить в виде 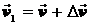. Ускорение точки в криволинейном движении характеризует быстроту изменения вектора 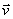по величине и направлению. Тогда средняя величина ускорения определится 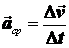, а мгновенное значение 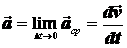, или

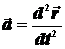(2.3)

48.Плоскопараллельное движение твердого тела. Уравнения плоскопараллельного движения.

Разложение движения на поступательное и вращательное

Плоскопараллельным (или плоским) называется такое движение твердого тела, при, котором все его точки перемещаются параллельно некоторой фиксированной плоскости П (рис. 1). Плоское движение совершают многие части механизмов и машин, например катящееся колесо на прямолинейном участке пути, шатун в кривошипно-ползунном механизме и др. Частным случаем плоскопараллельного движения является вращательное движение твердого тела вокруг неподвижной оси.

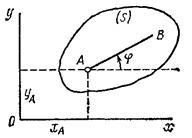
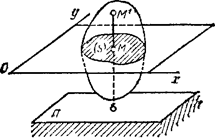
Рис.1 Рис.2

Рассмотрим сечение S тела какой-нибудь плоскости Оxy, параллельной плоскости П (рис.2). При плоскопараллельном движе­нии все точки тела, лежащие на прямой ММ’, перпендикулярной течению S, т. е. плоскости П, движутся тождественно.

Отсюда заключаем, что для изучения движения всего тела дос­таточно изучить, как движется в плоскости Оху сечение S этого тела или некоторая плоская фигура S. Поэтому в дальнейшем вместо плоского движения тела будем рассматривать движение плоской фигуры S в ее плоскости, т.е. в плоскости Оху.

Положение фигуры S в плоскости Оху определяется положением какого-нибудь проведенного на этой фигуре отрезка АВ (рис. 28). В свою очередь положение отрезка АВ можно определить, зная координаты x_A и y_A точки А и угол 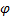, который отрезок АВ образует с осью х. Точку А, выбранную для определения положения фигуры S, будем в дальнейшем называть полюсом.

При движении фигуры величины x_A и y_A и 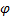будут изменяться. Чтобы знать закон движения, т. е. положение фигуры в плоскости Оху в любой момент времени, надо знать зависимости

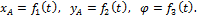
Уравнения, определяющие закон происходящего движения, называются уравнениями движения плоской фигуры в ее плоскости. Они же являются уравнениями плоскопараллельного движения твер­дого тела.

Первые два из уравнений движения определяют то движение, которое фигура совершала бы при 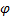=const; это, очевидно, будет поступательное движение, при котором все точки фигуры движутся так же, как полюс А. Третье уравнение определяет движе­ние, которое фигура совершала бы пр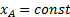и и 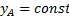, т.е. когда полюс А неподвижен; это будет вращение фи­гуры вокруг полюса А. Отсюда можно заключить, что в общем случае движение плоской фигуры в ее плоскости может рассматриваться как слагающееся из по­ступательного движения, при котором все точки фигуры движутся так же, как полюс А, и из вращательного движения вокруг этого полюса.

Основными кинематическими характеристиками рассматривае­мого движения являются скорость и ускорение поступательного движения, равные скорости и ускорению полюса 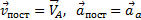, а также угловая скорость 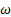и угловое ускорение 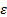враща­тельного движения вокруг полюса.