Предметы, из которых состоят соединения, называются элементами.

Предметы, из которых состоят соединения, называются элементами.

Различают три типа соединений: размещения, перестановки и сочетания.

Размещения

Размещениями из п элементов по т в каждом называются такие соединения, из которых каждое содержит т элементов, взятых из числа дан­ных n элементов, и которые отличаются друг от друга либо самими элементами (хотя бы одним), либо лишь порядком их расположения.

Число размещений из п элементов по т в каж­дом обычно обозначается символом А_n^m и вычисля­ется по следующей формуле*:

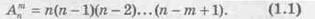
* Выводы формул для числа размещений, а в последующем изложении — для числа сочетаний, опускаются. Их можно найти в курсе элементарной алгебры.

Понятие факториала

Произведение п натуральных чисел от 1 до n обо­значается сокращенно п!, т. е. 1·2·3·...·(n -1)·n= n! (читается: п факториал). Например:

5!=1·2·3·4·5=120.

Считается, что0! = 1.

Используя понятие факториала, формулу(1.1)можно представить так:

где 0 „ т„ n.

Очевидно, что А_n¹= п (при m = 1) и А_n⁰=n (при m= 0).

Пример 1. Правление коммерческого банка вы­бирает из 10 кандидатов 3 человек на различныедолжности (все 10 кандидатов имеют равные шан­сы). Сколько всевозможных групп по 3 человека можно составить из 10 кандидатов?

Решение. В условии задачи речь идет о расчете числа комбинаций из 10 элементов по 3. Так как

группы по 3 человека могут отличаться и составом претендентов, и заполняемыми ими вакансиями, т. е. порядком, то для ответа необходимо рассчитать число размещений из 10 элементов по 3:

N=А³₁₀=10·9·8=720

Ответ. Можно составить 720 групп по 3 человека из 10.

Размещения с повторениями

Размещение с повторениями из n элементов по m(mn) элементов может содержать любой элемент сколько угодно раз от 1 до m включительно, или не содержать его совсем, т. е. каждое размещение с повторениями из n элементов по m элементов мо­жет состоять не только из различных элементов, но из m каких угодно и как угодно повторяющихся элементов.

Соединения, отличающиеся друг от друга хотя бы порядком расположения элементов, считаются различными размещениями.

Число размещений с повторениями из n элемен­тов по m элементов будем обозначать символом А_n^m_{(c повт.)} . Можно доказать, что оно равно n^m:

А_n^m_{(c повт.)} =n^m (1.3)

Пример 2. Изменим условие примера 1. Правле­ние коммерческого банка выбирает из 10 кандидатов 3 человек на 3 различные должности. Предпо­ложим, что один и тот же отобранный из 10 претендентов кандидат может занять не только одну, но и 2, и даже все 3 различные вакантные должности. Сколько в данном случае возможно комбинаций замещения 3 вакантных должностей?

Решение. Как и в предыдущей задаче, комби­нации замещения вакантных должностей могут отличаться и составом претендентов и заполняе­мыми ими вакансиями, т.е. порядком. Следовательно, и в этом случае для ответа на вопрос зада­чи необходимо рассчитать число размещений. Од­нако теперь вакантные должности могут замещать­ся одним и тем же претендентом, а значит, здесь речь идет о расчете числа размещений с повторе­ниями.

По условию задачи п = 10, т = 3. Следователь­но, А_n^m=10³=1000.

Ответ. Можно составить 1000 комбинаций.

Сочетания

Сочетаниями из п элементов по m в каждом называются такие соединения, из которых каж­дое содержит т элементов, взятых из числа дан­ных п элементов, и которые отличаются друг от друга по крайней мере одним элементом.

Число сочетаний из п элементов по m в каждом обозначается символом C_n^m и вычисляется так:

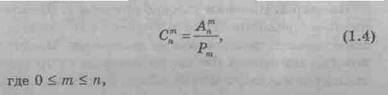
или

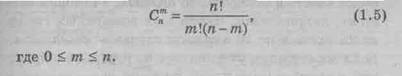
Пример 3. Правление коммерческого банка вы­бирает из 10 кандидатов 3 человек на одинаковые должности (все 10 кандидатов имеют равные шан­сы). Сколько всевозможных групп по 3 человека можно составить из 10 кандидатов?

Решение. Состав различных групп должен отли­чаться по крайней мере хотя бы одним кандидатом и порядок выбора кандидата не имеет значения, сле­довательно, этот вид соединений представляет собой сочетания. По условию задачи п = 10, т = 3. Подставив данные в формулу (1.5), получаем

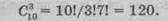
Ответ. Можно составить 120 групп из 3 человек по 10.

Замечание. Надо уметь различать сочетания от раз­мещений. Например: если в группе 25 студентов и 10 человек из них, выйдя из аудитории на перерыв, стоят вместе и беседуют, то порядок, в котором они стоят, несуществен. Число всех возможных групп из 25 человек по 10 в данном случае — сочетания. Если же студенты отправились на перерыве в буфет или в кассу за стипендией, то тогда существенно, в каком, порядке они стали, т. е. кто из них первый, второй и т. д. В этой ситуации при подсчете возможных групп из 25 человек по 10 необходимо состав­лять размещения.

Сочетания с повторениями

Сочетание с повторениями из n элементов по m (n Î m) элементов может содержать любой элемент сколько угодно раз от 1 до m включительно или не содержать его совсем, т. е. каждое сочетание из n элементов по m элементов может состоять не толь­ко из m различных элементов, но из m каких угод­но и как угодно повторяющихся элементов.

Следует отметить, что если, например, два со­единения по m элементов отличаются друг от друга только порядком расположения элементов, то они не считаются различными сочетаниями.

Число сочетаний с повторениями из n элементов по m будем обозначать символом (C_n^m)_{c повт} и вычислять по формуле

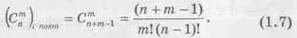
Замечание, т может быть и больше n.

Пример 4. Сколькими способами можно выбрать 6 пирожных в кондитерской, где есть 4 разных сорта пирожных?

Решение.

Ответ. Существует 84 различных способа выбора пирожных.

Перестановки

Перестановками из п элементов называются та­кие соединения, из которых каждое содержит все п элементов и которые отличаются друг от друга лишь порядком расположения элементов.

Число перестановок из п элементов обозначается символом P_n, это то же самое, что число размещений из п элементов по n в каждом, поэтому

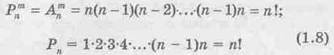
Пример 5. Менеджер ежедневно просматривает 6 изданий экономического содержания. Если порядок просмотра изданий случаен, то сколько суще­ствует способов его осуществления?

Решение. Способы просмотра изданий различа­ются только порядком, так как число, а значит, и состав изданий при каждом способе неизменны. Сле­довательно, при решении этой задачи необходимо рассчитать число перестановок.

По условию задачи п = 6. Следовательно,

Р_n = 6! =1·2·3·4·5·6 = 720.

Ответ. Можно просмотреть издания 720 способами.

Перестановки с повторениями

Число перестановок с повторениями выражает­ся формулой

Пример 6. Сколькими способами можно разде­лить т + п + s предметов на 3 группы, чтобы в одной группе было т предметов, в другой n пред­метов, в третьей — s предметов?

Решение.

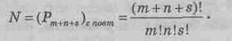
Вопрос 2

Вопрос 3

Вопрос4

Теорема сложения вероятностей несовместных событий. Следствие:Теорема сложения вероятностей совместных
событий.

Если события A и B несовместны, то вероятность суммы A+B равна сумме вероятностей этих событий: P(A+B)=P(A)+P(B).

Доказательство: Введем обозначения: n — общее число возможных элементарных исходов испытания; m1 — число исходов, благоприятствующих событию A; m2— число исходов, благоприятствующих событию В.

Число элементарных исходов, благоприятствующих наступлению либо события А, либо события В, равно m1 + m2. Следовательно,

Р (A + В) = (m1 + m2) / n = m1 / n + m2 / n.

Приняв во внимание, что m1 / n = Р (А) и m2 / n = Р (В), окончательно получим

Р (А + В) = Р (А) + Р (В).

Следствие:Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р (A1 + A2 + ... + An) = Р (A1) + Р (A2) + ... + Р (An).

Доказательство:Рассмотрим три события: А, В и С. Так как рассматриваемые события попарно несовместны, то появление одного из трех событий, А, В и С, равносильно наступлению одного из двух событий, A + В и С, поэтому в силу указанной теоремы

Р ( А + В + С) = Р [(А + В) + С] = Р (А + В) + Р (С) = Р (А) + Р (В) + Р (С).

Для произвольного числа попарно несовместных событий доказательство проводится методом математической индукции.

Вопрос 5

Следствие 1

Если событие А не зависит от события В, то и событие В не зависит от события А.

Доказательство:

Дано, что событие А не зависит от события В, т.е.

P(A) = P(A|B),

Требуется доказать, что и событие В не зависит от А, т.е.

P(B) = P(B|A),

При доказательстве будем предполагать, что P(A)№ 0.

Напишем теорему вероятностей в двух формах:

P(AB)=P(B)P(A|B),

P(AB)=P(A)P(B|A).

Откуда

P (A)P(B|A)=P(B)P(A|B)

Или так как событие А не зависит от В, т.е. P(A) = P(A|B), то

P(A)P(B|A)=P(B)P(A).

Разделим обе части равенства на P(A). Получим:

P(B|A)=P(B).

Что и требовалось доказать.

Итак, два события называются независимыми, если появление одного из них не изменяет вероятности появления другого.

Следствие2.

Вероятность произведения двух независимых событий равна произведению вероятностей этих событий.

При вычислении условной вероятности сужается пространство элементарных событий. Поясним это. Пусть задана некоторая полная группа событий w1, w2,w3,…,w n , несовместных и равновероятных между собой, и на основании ее установлены вероятности событий в множестве допустимых событий А,В и т.д. При вычислении условной вероятности решается вопрос, как должны измениться вероятности, если предположить, что станет достоверным наступление одного из допустимых событий, например А. Предположение, что стало достоверным событие А, нарушает заданную полную группу несовместных между событий w1, w2,w3,…,wn в том смысле, что благодаря этому предположению все события заданной группы уже не могут больше считаться равновероятными. А именно, предположение, что стало достоверным событие А, означает, что из всех событий w1, w2,w3,…,wn остаются возможными только те, на которые подразделяется А, остальные же становятся невозожными. z

4)Метод математической индукции позволяет обобщить эту формулу на случай n событий.

P(A₁A₂ x……x A_n)= P(A₁)P(A₂|A₁)x…x P(A_n|A₁A₂x…xA_n-1)

Вопрос 6

Формула полной вероятности

Пусть дана группа несовместных событий В1,В2…Вn и некоторое событие А, подразделяющееся на частные случаи АВ1, АВ2… АВn. И пусть даны вероятности P(В1), P(В2),…,P(Вn) и условные вероятности P(A|В1), P(A|В2),…,P(A|Bn). Требуется определить вероятность P(A).

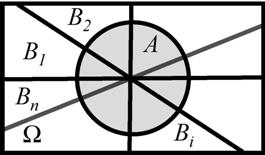
Рис. 2. Пояснение к формуле полной вероятности

Так как

A = АВ1 +АВ2 +…+ АВn,

То

P(A)= P(АВ1 + АВ2 +… +АВn ).

События В1, В2,…,Вn несовместные, следовательно, события АВ1,АВ2,…,АВn тоже несовместные. Воспользуемся теоремой сложения для несовместных событий.

P(A) = P(АВ1 + АВ2 +… +АВn) = P(АВ1)+ P(АВ2)+… +P(АВn )

По теореме умножения для каждого слагаемого имеем

P(ABi)=P(Bi)P(A|Bi).

Следовательно

P(A) = P(B1)P(A|B1) +P(B2)P(A|B2)+…+P(Bn)P(A|Bn).

Или

P(A) = 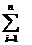P(B_i)P(A|B_i)

Вопрос 7

Теорема

Если производится n независимых испытаний, в каждом из которых событие А появится с вероятностью р, то вероятность того, что событие А появится ровноk раз в n испытаниях, выражается формулой

P_n(k) = C_n^kp^k (1 - p)^{n - k}

или

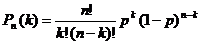
Эта формула называется формулой Бернулли.

Формула описывает, как распределяются вероятности между возможным числом появления событияA в n испытаниях.

Теорема

Если вероятность p появления события А в каждом испытании постоянна и отлична от нуля и единицы (0 < p < 1), то вероятность Pn(k) того, что событие А появится в n испытаниях ровно k раз, приближенно равна (тем точнее, чем больше n) значению функции

P(x)= 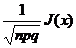, где

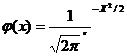
x=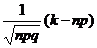

Значение функции 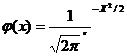находят по таблицам.

Функция j (x) четная, поэтому для отрицательных и положительных значений аргумента пользуются одними таблицами, т.е.

j (-x)=j (x).

Вопрос 8

Формула Пуассона

Часто интерес представляет случай большого числа n и малой вероятности p успеха в одном отдельном испытании. В этом случае удобно воспользоваться приближением Пуассона.

Теорема

Если вероятность p наступления события А в каждом испытании постоянна, близка к нулю, а число независимых испытаний n достаточно велико, то вероятность P_n(k) того, что в n независимых испытаниях событие А наступит k раз, приближенно равна:

P_n(k) = (l^ke^-l )/k!

где l = np.

Эта формула называется формулой Пуассона. Обычно приближенную формулу Пуассона применяют, когда р <0,1, а npq < 10.

Функция (l^k e^-l )/ k! затабулирована, т.е. имеет таблицу.

Значения функции (l^k e^-l )/ k!

k
	0,36	0,27	0,0337	0,0027
	0,18	0,27	0,084	0,0107
	0,06	0,18	0,14	0,028
	0,0031	0,036	0,175	0,0916

Формула Пуассона используется в задачах, относящихся к редким событиям.

Вопрос 9

Понятие случайной величины. Дискретная случайная величина. Закон распределения дискретной случайной
величины. Функция распределения дискретной случайной величины.

Понятие случайной величины

Случайной величиной (СВ) называют такую величину, которая в результате опыта может принимать те или иные значения, причем до опыта мы не можем сказать какое именно значение она примет. (Более точно, СВ - это действительная функция, определенная на пространстве элементарных событий W).

Строго понятие "случайная величина" определяется так:

Пусть имеется пространство элементарных событий U, на нем построено поле событий и для каждого события А из этого поля определена вероятность Р(А). Каждому элементарному событию gi из U сопоставим число ξi. Потребуем, чтобы для любого х (-∞ < x < +∞) множество А тех g, для которых ξ < x , принадлежало полю событий, т.е. для него определена вероятность Р{ξ < x} = P(A) = F(x). Тогда ξ называется случайной величиной, а F(x) - ее функцией распределения.

Проще можно сказать, что случайная величина - это величина, значение которой зависит от случая, если для всех х известна функция распределения F(x), т.е. вероятность того, что это значение меньше х.

В строгом определении задание пространства элементарных событий означает по существу задание условий, в которых возникают те или иные значения случайной величины, а если эти условия заданы, то тем самым определена и F(x). Например, нельзя сказать, что "температура - случайная величина". Но "температура воздуха, измеряемая на данной метеостанции в случайный момент времени в течение года" - случайная величина, "температура воздуха в случайно выбранной точке земного шара 1 января 2001г. в 12.00 по Московскому времени" - другая случайная величина.

Свойства функции распределения:

1) F(-∞) = 0

2) F(+∞) = 1

3) F(x) - не убывающая функция х

Случайные величины могут быть непрерывными, т.е. принимать любые значения в некотором интервале (например, упомянутые выше температуры). У них F(x) - непрерывная функция.

Дискретная случайная величина.

Случайные величины могут быть дискретными т.е. принимать только конечное или счетное множество определенных значений (например, число очков при бросании игральной кости; число телефонных звонков, поступающих конкретному абоненту в течение суток). У таких величин F(x) имеет разрывы в точках, соответствующих принимаемым значениям. Такие величины удобнее характеризовать указанием возможных значений и их вероятностей.

Пример 1: число очков при бросании кости

Значения х_i: 1 2 3 4 5 6

Вероятности р(х_i) 1/6 1/6 1/6 1/6 1/6 1/6

Функция распределения:

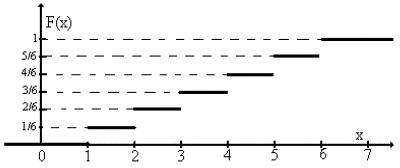
Рисунок 5.1 Функция распределения числа очков при бросании кости

Обратите внимание: Хотя случайная величина принимает только дискретные значения ее функция распределения определена для любых х.

Например: F(-1) = 0, F(0) = 0, F(0.999) = 0, F(1.001) = 1/6, F(3.5) = 3/6, F(7) = 1.

Для непрерывных случайных величин вводится понятие плотностираспределения р(х), которая есть производная от функци распределения.

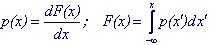
Вероятность того, что случайная величина ξ примет значение, лежащее в интервале (а,b) равна разности значений функции распределения на концах интервала

P{ a≤ ξ <b } = F(b) - F(a)

Для непрерывных случайных величин

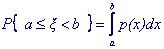
Важно помнить, что всегда для дискретных распределений сумма р(хi) по всем возможным значениям х_i равна 1;

для непрерывных распределений

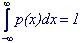
Закон распределения дискретной случайной
величины.

Пусть X - дискретная случайная величина, которая принимает значения х1, х2,..., xn,... с некоторой вероятностью pi, где i = 1, 2,..., n,... Тогда можно говорить о вероятности того, что случайная величина X приняла значение хi: рi=Р(Х=хi).

Значения xi и соответствующие Pi представляют в виде таблицы:

x_i x₁ x₂ x₃ ... x_n ...

p_i p₁ p₂ p₃ ... p_n ...

Эта таблица является одной из форм задания ДСВ.

Обычно случайные величины располагаются в возрастающем порядке.

Основное свойство таблицы заключено в том, что сумма вероятностей равна 1:

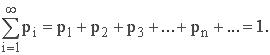
Дискретная случайная величина может также представляться в виде многоугольника распределения - фигуры, состоящей из точек (х_i, р_i), соединенных отрезками (рис. 6).

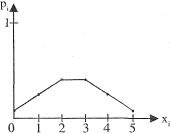
Рис. 6. Многоугольник распределения

Над случайными величинами устанавливаются операции сложения и умножения.

1) Суммой двух случайных величин X и Y называется случайная величина, которая получается в результате сложения всех значений случайной величины X и всех значений случайной величины Y, соответствующие вероятности перемножаются.

1) Произведением двух случайных величин X и Y называется случайная величина, которая получается в результате перемножения всех значений случайной величины X и всех значений случайной величины Y, соответствующие вероятности перемножаются.

Вопрос 10

Математическое ожидание дискретной случайной величины. Свойства математического ожидания. Дисперсия
дискретной случайной величины и ее свойства.

Вопрос 11

Основные законы распределения вероятностей дискретной случайной величины: Бернулли, биномиальное,
геометрическое, распределение Пуассона, (гипергеометрическое)

Распределение Бернулли

Если производится серия независимых испытаний, в каждом из который событие А может появиться с одинаковой вероятностью р, то число появлений события есть случайная величина, распределенная по закону Бернулли, или по биномиальному закону (другое название распределения).

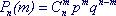
Здесь n - число испытаний в серии, m - случайная величина (число появлений события А), Р_n(m) - вероятность того, что А произойдет именно m раз, q = 1 - р (вероятность того, что А не появится в испытании).

Пример 1: Кость бросают 5 раз, какова вероятность того, что 6 очков выпадет дважды ?

n = 5, m = 2, p = 1/6, q = 5/6

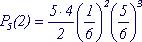
Параметры распределения: n , р

Биномиальный закон распределения. Случайная величина X принимает значения О, 1, 2, 3, 4, 5,..., n, с вероятностью, определяемой по формуле Бернулли (1.10.1):

xi				…	k	…	n
pi				…		…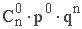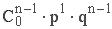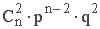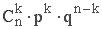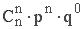

Вопрос 12

Вопрос 13

Вопрос 14

Вопрос 15

Числовые характеристики случайной величины: центральные и начальные моменты, среднее квадратическое
отклонение, мода и медиана, асимметрия и эксцесс, квантиль, процентная точка.

Начальный момент к-го порядка случайной величины Х есть математическое ожидание к-ой степени этой случайной величины:

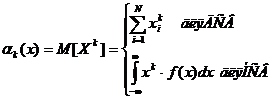
При К=0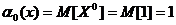

К=1 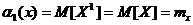- математическое ожидание;

К=2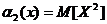

Центрированной случайной величиной 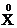называется случайная величина, математическое ожидание которой находится в начале координат(в центре числовой оси), т.е М[ 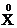]=0

Операция центрирования(переход от нецентрированной величины Х к центрированной )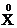

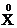=Х – m_x

Центральный момент порядка k случайной величины X есть математическое ожидние k-й степени центрированой случайной величины :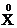

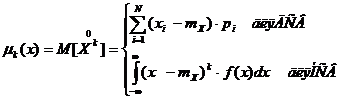
При К=0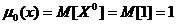

К=1 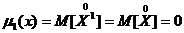- математическое ожидание;

К=2 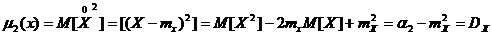-дисперсия.

Среднее квадратическое отклонениеслучайной величины Х характеризует ширину диапазона значений Х и равно:

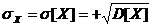
СКО измеряются в тех же физических единицах, что и случайная величины.

Правило 3 .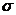

[ ]

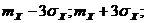Математическое ожидание и дисперсия (или СКО)- наиболее часто применяемые характеристики случайной величины. Они характеризуют наиболее важные черты распределения: его положение и степень разбросанности значений. Для более подробного описания используются начальные и центральные моменты высших порядков. Кроме математического ожидания на практике часто применяются и другие характеристики положения распределения значений.

Модаслучайной величины равна ее наиболее вероятному значению, т.е. то значение, для которого вероятность p_i (для дискретной случайной величины) или F(x) (для непрерывных случайных величины) достигает максимума:

F(x=max), p(X=M₀)= max

Распределение с одним максимумом плотности распределения называется «универсальным». Если многоугольник распределения или кривая распределения имеют более одного максимума, распределение называют «полимодальным». Если распределение обладает не максимумом, а минимумом, то оно называется «антимодальным».

Медианаслучайной величины Х равна такому ее значению, для которого выполняется условие p{X<Me}=p{X 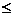Me}. Медиана , как правило, существует только для непрерывных случайных величин. Значение Me может быть определено как решение одного из следующих

Уравнений:

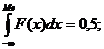
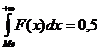
F(Me)= 0,5

В точке Me площадь, ограниченная кривой распределения, делится пополам.

Квантиль 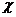_pслучайной величины Х- это такое ее значение, для которого выполняется условие

P{X<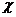 _p }=F( 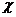_p )=p

Очевидно, что медиана – это квантиль 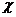_0,5.

Предметы, из которых состоят соединения, называются элементами.

Различают три типа соединений: размещения, перестановки и сочетания.

Размещения

Размещениями из п элементов по т в каждом называются такие соединения, из которых каждое содержит т элементов, взятых из числа дан­ных n элементов, и которые отличаются друг от друга либо самими элементами (хотя бы одним), либо лишь порядком их расположения.

Число размещений из п элементов по т в каж­дом обычно обозначается символом А_n^m и вычисля­ется по следующей формуле*:

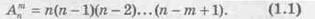
* Выводы формул для числа размещений, а в последующем изложении — для числа сочетаний, опускаются. Их можно найти в курсе элементарной алгебры.

Понятие факториала

Произведение п натуральных чисел от 1 до n обо­значается сокращенно п!, т. е. 1·2·3·...·(n -1)·n= n! (читается: п факториал). Например:

5!=1·2·3·4·5=120.

Считается, что0! = 1.

Используя понятие факториала, формулу(1.1)можно представить так:

где 0 „ т„ n.

Очевидно, что А_n¹= п (при m = 1) и А_n⁰=n (при m= 0).

Пример 1. Правление коммерческого банка вы­бирает из 10 кандидатов 3 человек на различныедолжности (все 10 кандидатов имеют равные шан­сы). Сколько всевозможных групп по 3 человека можно составить из 10 кандидатов?

Решение. В условии задачи речь идет о расчете числа комбинаций из 10 элементов по 3. Так как

группы по 3 человека могут отличаться и составом претендентов, и заполняемыми ими вакансиями, т. е. порядком, то для ответа необходимо рассчитать число размещений из 10 элементов по 3:

N=А³₁₀=10·9·8=720

Ответ. Можно составить 720 групп по 3 человека из 10.

Размещения с повторениями

Размещение с повторениями из n элементов по m(mn) элементов может содержать любой элемент сколько угодно раз от 1 до m включительно, или не содержать его совсем, т. е. каждое размещение с повторениями из n элементов по m элементов мо­жет состоять не только из различных элементов, но из m каких угодно и как угодно повторяющихся элементов.

Соединения, отличающиеся друг от друга хотя бы порядком расположения элементов, считаются различными размещениями.

Число размещений с повторениями из n элемен­тов по m элементов будем обозначать символом А_n^m_{(c повт.)} . Можно доказать, что оно равно n^m:

А_n^m_{(c повт.)} =n^m (1.3)

Пример 2. Изменим условие примера 1. Правле­ние коммерческого банка выбирает из 10 кандидатов 3 человек на 3 различные должности. Предпо­ложим, что один и тот же отобранный из 10 претендентов кандидат может занять не только одну, но и 2, и даже все 3 различные вакантные должности. Сколько в данном случае возможно комбинаций замещения 3 вакантных должностей?

Решение. Как и в предыдущей задаче, комби­нации замещения вакантных должностей могут отличаться и составом претендентов и заполняе­мыми ими вакансиями, т.е. порядком. Следовательно, и в этом случае для ответа на вопрос зада­чи необходимо рассчитать число размещений. Од­нако теперь вакантные должности могут замещать­ся одним и тем же претендентом, а значит, здесь речь идет о расчете числа размещений с повторе­ниями.

По условию задачи п = 10, т = 3. Следователь­но, А_n^m=10³=1000.

Ответ. Можно составить 1000 комбинаций.

Сочетания

Сочетаниями из п элементов по m в каждом называются такие соединения, из которых каж­дое содержит т элементов, взятых из числа дан­ных п элементов, и которые отличаются друг от друга по крайней мере одним элементом.

Число сочетаний из п элементов по m в каждом обозначается символом C_n^m и вычисляется так:

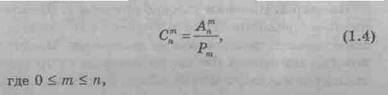
или

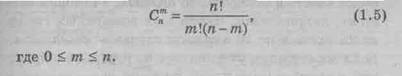
Пример 3. Правление коммерческого банка вы­бирает из 10 кандидатов 3 человек на одинаковые должности (все 10 кандидатов имеют равные шан­сы). Сколько всевозможных групп по 3 человека можно составить из 10 кандидатов?

Решение. Состав различных групп должен отли­чаться по крайней мере хотя бы одним кандидатом и порядок выбора кандидата не имеет значения, сле­довательно, этот вид соединений представляет собой сочетания. По условию задачи п = 10, т = 3. Подставив данные в формулу (1.5), получаем

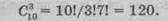
Ответ. Можно составить 120 групп из 3 человек по 10.

Замечание. Надо уметь различать сочетания от раз­мещений. Например: если в группе 25 студентов и 10 человек из них, выйдя из аудитории на перерыв, стоят вместе и беседуют, то порядок, в котором они стоят, несуществен. Число всех возможных групп из 25 человек по 10 в данном случае — сочетания. Если же студенты отправились на перерыве в буфет или в кассу за стипендией, то тогда существенно, в каком, порядке они стали, т. е. кто из них первый, второй и т. д. В этой ситуации при подсчете возможных групп из 25 человек по 10 необходимо состав­лять размещения.

Сочетания с повторениями

Сочетание с повторениями из n элементов по m (n Î m) элементов может содержать любой элемент сколько угодно раз от 1 до m включительно или не содержать его совсем, т. е. каждое сочетание из n элементов по m элементов может состоять не толь­ко из m различных элементов, но из m каких угод­но и как угодно повторяющихся элементов.

Следует отметить, что если, например, два со­единения по m элементов отличаются друг от друга только порядком расположения элементов, то они не считаются различными сочетаниями.

Число сочетаний с повторениями из n элементов по m будем обозначать символом (C_n^m)_{c повт} и вычислять по формуле

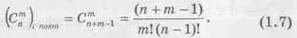
Замечание, т может быть и больше n.

Пример 4. Сколькими способами можно выбрать 6 пирожных в кондитерской, где есть 4 разных сорта пирожных?

Решение.

Ответ. Существует 84 различных способа выбора пирожных.

Перестановки

Перестановками из п элементов называются та­кие соединения, из которых каждое содержит все п элементов и которые отличаются друг от друга лишь порядком расположения элементов.

Число перестановок из п элементов обозначается символом P_n, это то же самое, что число размещений из п элементов по n в каждом, поэтому

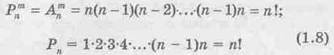
Пример 5. Менеджер ежедневно просматривает 6 изданий экономического содержания. Если порядок просмотра изданий случаен, то сколько суще­ствует способов его осуществления?

Решение. Способы просмотра изданий различа­ются только порядком, так как число, а значит, и состав изданий при каждом способе неизменны. Сле­довательно, при решении этой задачи необходимо рассчитать число перестановок.

По условию задачи п = 6. Следовательно,

Р_n = 6! =1·2·3·4·5·6 = 720.

Ответ. Можно просмотреть издания 720 способами.

Перестановки с повторениями

Число перестановок с повторениями выражает­ся формулой

Пример 6. Сколькими способами можно разде­лить т + п + s предметов на 3 группы, чтобы в одной группе было т предметов, в другой n пред­метов, в третьей — s предметов?

Решение.

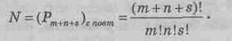
Вопрос 2