О случайных событиях с вероятностями близкими к 0 или к 1

При решении многих практических задач приходится иметь дело с событиями, вероятность которых очень мала, т.е. близка к нулю. На основании опыта в отношении таких событий принят следующий принцип. Если случайное событие имеет очень малую вероятность, то практически можно считать, что в единичном испытании оно не наступит, иначе говоря, возможностью его появления можно пренебречь. Ответ на вопрос,насколькомалойдолжна быть эта вероятность, определяется существом решаемых задач, тем, насколько важен для нас результат предсказания. Например, если вероятность того, что парашют при прыжке не раскроется равна 0,01, то применение таких парашютов недопустимо. Однако равная той же 0,01 вероятность того, что поезд дальнего следования прибудет с опозданием, делает нас практически уверенными в том, что он прибудет вовремя.

Достаточно малую вероятность, при которой (в данной конкретной задаче) событие можно считать практически невозможным, называют уровнем значимости.На практике уровень значимости обычно принимают равным 0,01 (однопроцентный уровень значимости) или 0,05 (пятипроцентный уровень значимости), намного реже он берется равным 0,001.

Введение уровня значимости позволяет утверждать, что если некоторое событие А практически невозможно, то противоположное событие 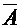- практически достоверно, т.е. для него Р( 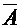) » 1.

Глава II. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Случайные величины, их виды

В математике величина – это общее название различных количественных характеристик предметов и явлений. Длина, площадь, температура, давление и т.д. – примеры разных величин.

Величина, которая принимает различные числовые значения под влиянием случайных обстоятельств, называется случайной величиной. Примеры случайных величин: число больных на приеме у врача; точные размеры внутренних органов людей и т.д.

Различаютдискретные инепрерывные случайные величины.

Случайная величина называется дискретной, если она принимает только определенные отделенные друг от друга значения, которые можно установить и перечислить.

Примерами дискретной случайной величиной являются:

– число студентов в аудитории – может быть только целым положительным числом: 0,1,2,3,4….. 20…..;

– цифра, которая появляется на верхней грани при бросании игральной кости – может принимать лишь целые значения от 1 до 6;

– относительная частота попадания в цель при 10 выстрелах – ее значения: 0; 0,1; 0,2; 0,3 …1

– число событий, происходящих за одинаковые промежутки времени: частота пульса, число вызовов скорой помощи за час, количество операций в месяц с летальным исходом и т.д.

Случайная величина называется непрерывной, если она может принимать любые значения внутри определенного интервала, который иногда имеет резко выраженные границы, а иногда – нет*. К непрерывным случайным величинам относятся, например, масса тела и рост взрослых людей, масса тела и объем мозга, количественное содержание ферментов у здоровых людей, размеры форменных элементов крови, рН крови и т.п.

Понятие случайной величины играет определяющую роль в современной теории вероятностей, разработавшей специальные приемы перехода от случайных событий к случайным величинам.

Если случайная величина зависит от времени, то можно говорить о случайном процессе.