Вероятность случайного события

Каждая наука, развивающая общую теорию какого-либо круга явлений, базируется на ряде основных понятий. Например, в геометрии – это понятия точки, прямой линии; в механике – понятия силы, массы, скорости и т.д. Основные понятия существуют и в теории вероятностей, одно из них – случайное событие.

Случайное событие – это всякое явление (факт), которое в результате опыта (испытания) может произойти или не произойти.

Случайные события обозначаются буквами А, В, С … и т.д. Приведем несколько примеров случайных событий:

А –выпадение орла (герба) при подбрасывании стандартной монеты;

В – рождение девочки в данной семье;

С – рождение ребенка с заранее заданной массой тела;

D – возникновение эпидемического заболевания в данном регионе в определенный период времени и т.д.

Основной количественной характеристикой случайного события является его вероятность. Пусть А – какое-то случайное событие. Вероятность случайного события А – это математическая величина, которая определяет возможность его появления. Она обозначается Р(А).

Рассмотрим два основных метода определения данной величины.

Классическое определение вероятности случайного событияобычно базируется на результатах анализа умозрительныхопытов (испытаний), суть которых определяется условием поставленной задачи. При этом вероятность случайного события Р(А)равна:

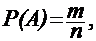(1)

где m – число случаев, благоприятствующих появлению события А; n – общее число равновозможных случаев.

Пример 1. Лабораторная крыса помещена в лабиринт, в котором лишь один из четырех возможных путей ведет к поощрению в виде пищи. Определите вероятность выбора крысой такого пути.

Решение: по условию задачи из четырех равновозможных случаев (n=4) событию А (крыса находит пищу)
благоприятствует только один, т.е. m = 1 Тогда Р(А) = Р (крыса находит пищу) = 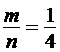= 0,25= 25%.

Пример 2. В урне 20 черных и 80 белых шаров. Из нее наугад вынимается один шар. Определите вероятность того, что этот шар будет черным.

Решение: количество всех шаров в урне – это общее число равновозможных случаев n, т.е. n = 20 + 80 =100, из них событие А (извлечение черного шара) возможно лишь в 20, т.е. m = 20. Тогда Р(А) = Р(ч.ш.) = 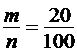= 0,2 = 20%.

Перечислим свойства вероятности следующие из ее классического определения – формула (1):

1. Вероятность случайного события – величина безразмерная.

2. Вероятность случайного события всегда положительна и меньше единицы, т.е. 0 < P (A) < 1.

3. Вероятность достоверного события, т.е. события, которое в результате опыта обязательно произойдет (m = n), равна единице.

4. Вероятность невозможного события (m = 0) равна нулю.

5. Вероятность любого события – величина не отрицательная и не превышающая единицу:
0 £ P (A) £ 1.

Статистическое определение вероятности случайного событияприменяется тогда, когда невозможно использоватьклассическое определение (1). Это часто имеет место в биологии и медицине. В таком случае вероятность Р(А) определяют путем обобщения результатовреально проведенных серий испытаний (опытов).

Введем понятие относительной частоты появления случайного события. Пусть была проведена серия, состоящая из N опытов (число N может быть выбрано заранее); интересующее нас событие А произошло в М из них (M < N). Отношение числа опытов М, в которых произошло это событие, к общему числу проведенных опытов N называютотносительной частотой появления случайного события А в данной серии опытов – Р^* (А)

Р^* (А) = .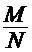

Экспериментально установлено, что если серии испытаний (опытов) проводятся в одинаковых условиях и в каждой из них число N достаточно велико, то относительная частота обнаруживает свойство устойчивости: от сериик серии онаменяетсямало,приближаясь c увеличением числа опытовк некоторой постояннойвеличине. Ееи принимают за статистическуювероятность случайного события А:

Р(А) = lim 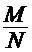, при N , (2)

Итак, статистической вероятностью Р(А) случайного события А называют предел, к которому стремится относительная частота появления этого события при неограниченном возрастании числа испытаний (при N → ∞).

Приближенно статистическая вероятность случайного события равна относительной частоте появления этого события при большом числе испытаний:

Р(А) ≈ Р^* (А) = 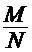(при больших N) (3)

Например, в опытах по бросанию монеты относительная частота выпадения герба при 12000 бросаний оказалась равной 0,5016, а при 24000 бросаний – 0,5005. В соответствии с формулой (1):

P(герб) = 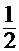= 0,5 = 50%

Пример. При врачебном обследовании 500 человек у 5 из них обнаружили опухоль в легких (о.л.). Определите относительную частоту и вероятность этого заболевания.

Решение: по условию задачи М = 5, N = 500, относительная частота Р^*(о.л.) = М/N = 5/500 = 0,01; поскольку N достаточно велико, можно с хорошей точностью считать, что вероятность наличия опухоли в легких равна относительной частоте этого события:

Р(о.л.) = Р^*(о.л.) = 0,01 = 1%.

Перечисленные ранее свойства вероятности случайного события сохраняются и при статистическом определении данной величины.