Синтез регулятора основного контура

Упростим передаточную функцию Wзам2(р) замкнутого подчиненного контура, отбросив в ней слагаемое 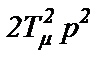с малым коэффициентом 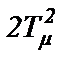из-за малости в нем Тμ

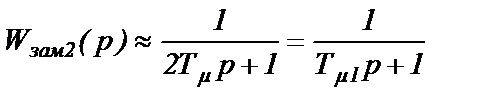, (3.7)

где Тμ1 – малая постоянная времени для основного контура, которая вдвое больше малой постоянной времени Тμ подчиненного контура.

Примем желаемую передаточную функцию разомкнутого контура вида

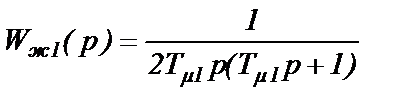(3.8)

В соответствии с (2.6) рассчитываем

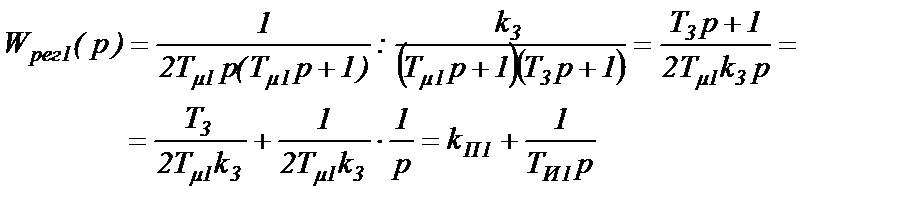(3.9)

Это ПИ-регулятор. Д-части в нем нет.

Динамические показатели качества для регулируемого сигнала у имеют значения

tp=4,7 Тμ1=9,4 Тμ , σ1=4,3 %, (3.10)

а статическая ошибка регулирования равна нулю.

Теперь нужно обосновать допустимость упрощения (3.7). Обоснование следующее: если рассчитать в синтезированной САУ переходный процесс для сигнала у, используя сначала точное значение Wзам2(р) (3.5), а затем приближенное (3.7), то окажется, что различие в показателях качества tp и σ1 обоих переходных процессов не превысит 5%. Такая погрешность вполне допустима в инженерных расчетах, и, поэтому, упрощение (3.7) обосновано.

Аналогичные расчеты нужно выполнить в случае настройки основного контура на симметричный оптимум, используя в качестве желаемой передаточной функции разомкнутого контура выражение (2.10).

Модель ЭП с двигателем постоянного тока

независимого возбуждения с жесткими связями

На функциональной схеме (рис.4.1а) показаны электрические цепи ДПТ и нагрузка с моментом сопротивления МС и моментом инерции J.

Далее будем рассматривать ДПТ с управлением им по цепи якоря с помощью напряжения uЯ при постоянстве напряжения uВ на обмотке возбуждения.

Система уравнений, описывающая элементы функциональной схемы:

uЯ=е+LЯрiЯ+ RЯiЯ - уравнение цепи якоря двигателя;

е=СФ·ω - определение э.д.с. вращения;

Jрω=М-МС - уравнение механики ЭП; (4.1)

М=СФiЯ - определение вращающего момента ДПТ.

Входными сигналами (сигналами-аргументами) модели ДПТ (4.1) являются uЯ и МС. Остальные сигналы е, iЯ, ω и М являются сигналами-функциями, зависящими от сигналов-аргументов. Так как при четырех сигналах-функциях имеем систему из 4-х уравнений, то любой из этих сигналов может быть однозначно выражен через сигналы-аргументы. Это можно сделать двумя способами: решив систему уравнений относительно заданного сигнала-функции, либо с использование структурных схем ЭП с ДПТ. Учитывая то, что в последующих вопросах будут активно использоваться структурные схемы, выберем второй способ.

Преобразуем систему уравнений (4.1) 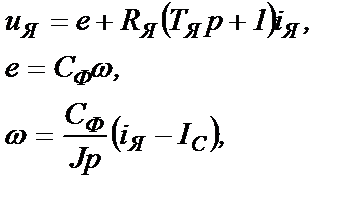(4.2)

где 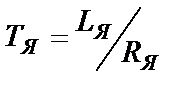- электрическая постоянная времени цепи якоря;

ІС – ток сопротивления нагрузки, определяемый из равенства МС=СФIC .

Структурная схема ЭП, построенная по уравнениям системы (4.2), приведена на рис.4.1б.

В исследованиях широко используется структурная схема на рис.4.1в. Для ее обоснования сначала преобразуем 3-е уравнение системы (4.2)

, (4.3)

где 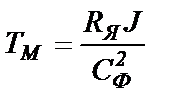- механическая постоянная времени ЭП.

По системе уравнений

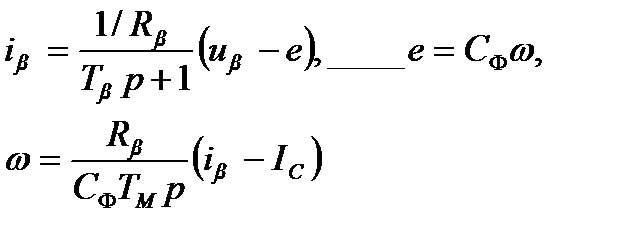(4.4)

составлена структурная схема, приведенная на рис.4.1в.

Сворачиваем структурную схему на рис.4.1в:

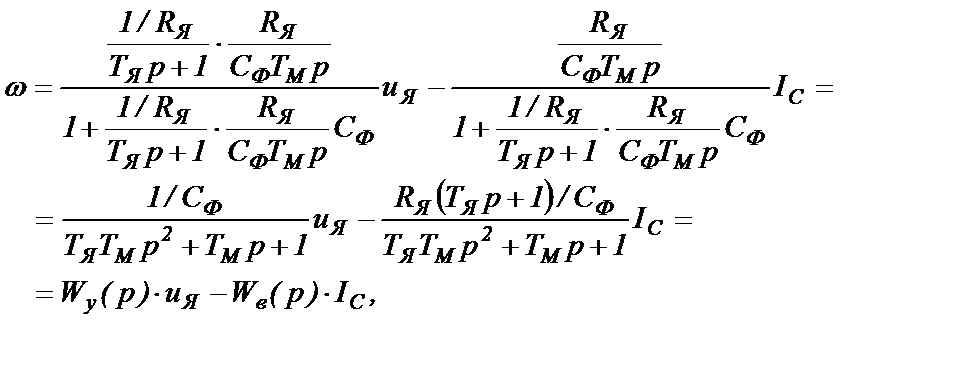(4.5)

где Wy(p) и Wв(p) – передаточные функции ЭП по управлению и возмущению.

Используя Wy(p) и Wв(p), можно рассчитать реакцию ЭП на изменения напряжения якоря uЯ и на изменения тока сопротивления IC нагрузки.

Переходный процесс при изменении только uЯ определяется из операторного выражения

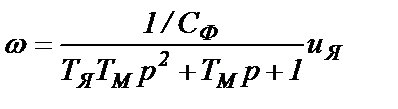(4.6)

Вид переходного процесса зависит от вида корней характеристического уравнения

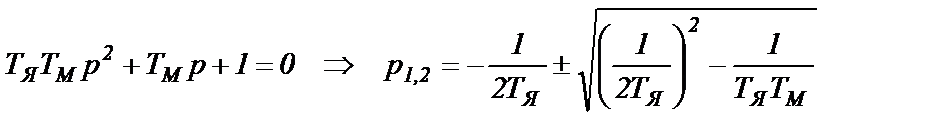(4.7)

При 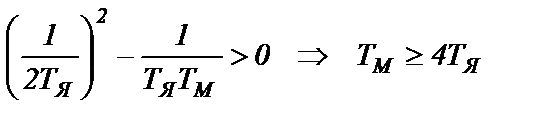(инерционный ЭП) переходный процесс апериодический 2-го порядка, а при 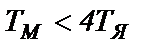(малоинерционный ЭП) переходный процесс колебательный.

Аналогичная реакция ЭП на изменения момента сопротивления нагрузки.

4.18. Поясните смысл координатных преобразований неподвижных обмоток трехфазной электрической машины к двухфазной электрической машине, обмотки которой вращаются с произвольной частотой. Приведите уравнения электрического состояния АД в осях α-β и выражения потокосцеплений обмоток. В чем преимущество двухфазной модели АД перед трехфазной?

Конструктивными электрическими компонентами АД являются три обмотки статора и обмотки ротора, которые для АД с фазным ротором содержат также три обмотки, а для АД с короткозамкнутым ротором количество обмоток может составлять несколько десятков.

Вычисляем составляющие потокосцепления Ψ1А через токи катушек

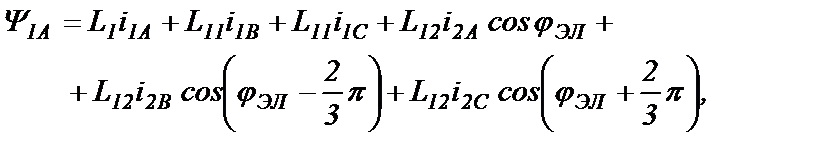(20.2)

где L1 – собственная индуктивность катушки фазы статора;

L11 – взаимная индуктивность катушек статора;

L12 – взаимная индуктивность между катушками статора и ротора при совпадении осей этих катушек.

Полные потокосцепления всех других катушек определяются по формулам подобным (20.2).

Выражение (20.2) является нелинейным из-за того, что в 4-м, 5-м и 6-м слагаемых содержатся произведения переменных – токов обмоток ротора i2 и тригонометрических функций от угла φЭЛ.

При известных полных потокосцеплениях всех обмоток и известных активных сопротивлениях обмоток статора R1 и ротора R2 система дифференциальных уравнений обмоток АД имеет вид

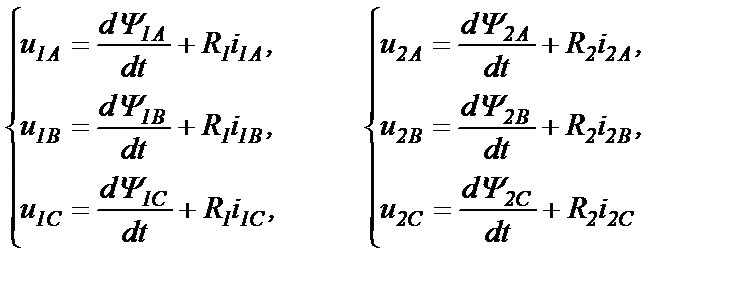
Недостатки математической модели АД в физических переменных:

1) минимальное число дифференциальных уравнений равно шести (20.3);

2) выражения полных потокосцеплений каждой обмотки содержат минимум по шесть слагаемых (20.2);

3) система дифференциальных уравнений (20.3) нелинейная.

1-й и 2-й недостатки математической модели АД в физических переменных устраняются путем перехода к модели АД, в которой статор и ротор представлены в виде двух взаимно перпендикулярных катушек.

В основе двухфазной модели лежит понятие вращающегося обобщенного вектора. Вектор некоторой совокупности физических сигналов называется обобщенным, если его проекции на выбранные оси являются мгновенными значениями физических сигналов.

На рис.21.1 в верхнем ряду показаны оси трех- и двухфазных обмоток, а в нижнем – эквивалентирование обмоток статора и ротора.

Двухфазные оси α-β статора неподвижны в пространстве, причем ось α совмещена с осью обмотки 1А статора. Двухфазные оси d-q ротора вращаются в пространстве вместе ротором с частотой ωЭЛ, причем ось d совмещена с осью обмотки 2А ротора. Обобщенный вектор потокосцепления 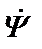(или напряжения, или тока) вращается в пространстве с частотой ω1 напряжения питания статора АД. Проекции 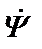на оси обмоток статора являются мгновенными значениями потокосцеплений этих обмоток, что доказывается вычислениями по построениям на рис.21.1:

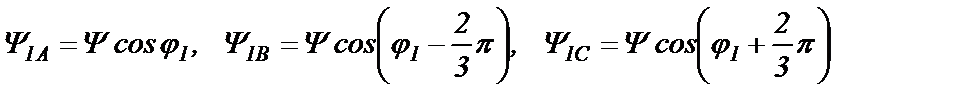(21.1)

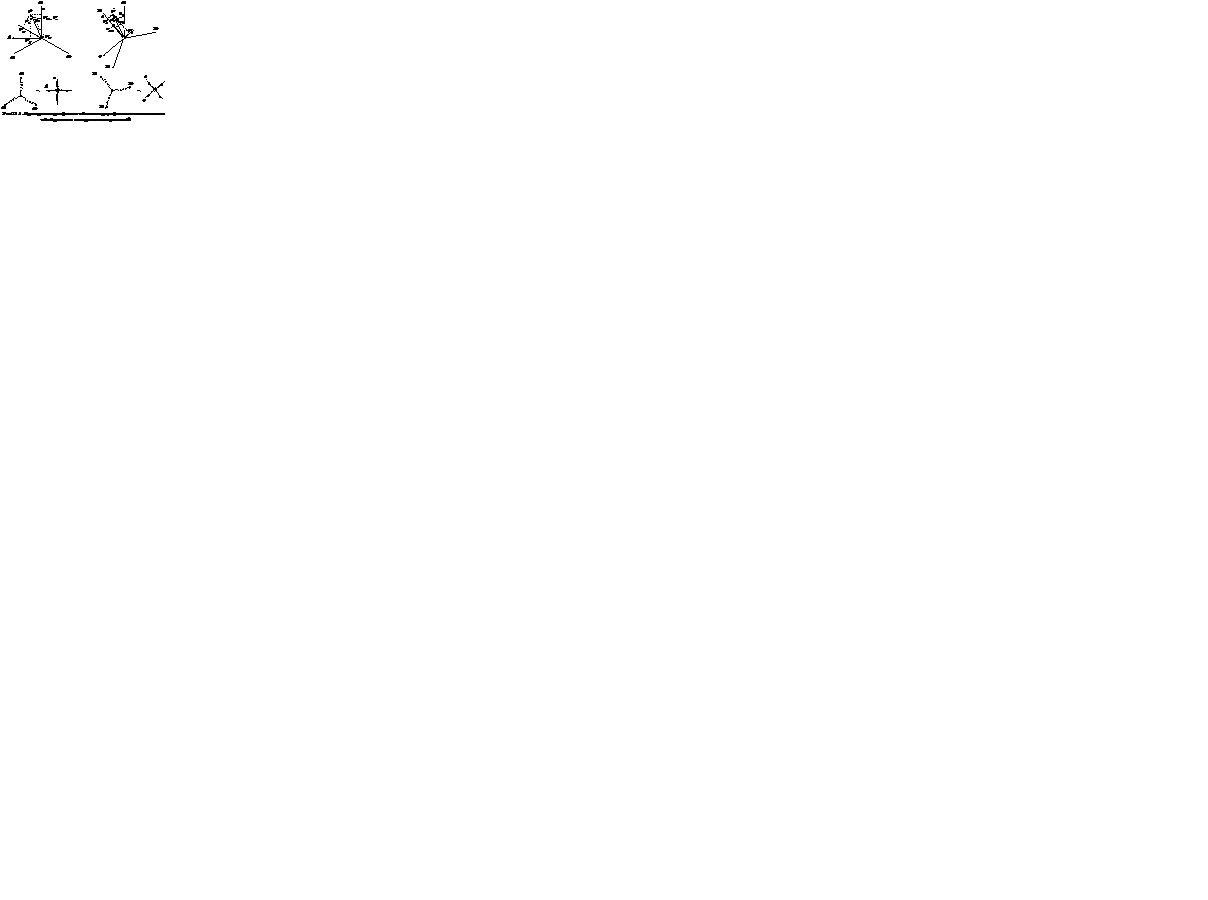
Проекции 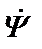на оси α-β являются мгновенными значениями потокосцеплений по этим осям, что доказывается вычислениями:

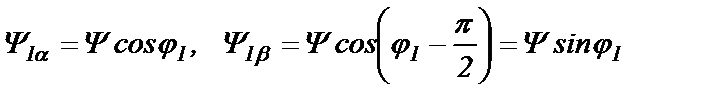(21.2)

Можно утверждать обратное, что потокосцепления трехфазных обмоток, определяемые формулами (21.1), и потокосцепления двухфазных обмоток, определяемые формулами (21.2), дают одно и то же результирующее потокосцепление 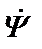статора. Значит, после подмены реальной трехфазной обмотки на двухфазную с взаимно-перпендикулярными осями α и β, результирующее потокосцепление статора, которое вращается в пространстве с частотой ω1, работа АД не изменится.

Точно также можно заменить трехфазную обмотку ротора, а также многофазную обмотку короткозамкнутого ротора, на двухфазную обмотку с взаимно-перпендикулярными осями d и q. Потокосцепления таких обмоток согласно рис.21.1 вычисляются по формулам:

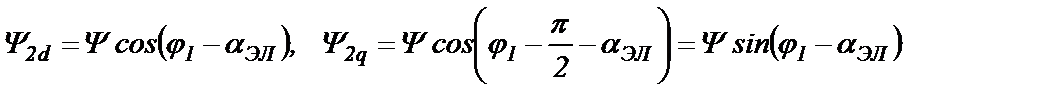(21.3)

Теперь можно составить систему дифференциальных уравнений для АД с двухфазными обмотками статора и ротора

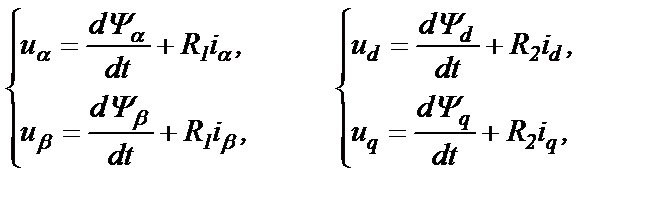(21.4)

где суммарные потокосцепления Ψα, Ψβ, Ψd и Ψq всех четырех двухфазных обмоток с учетом построений на рис.21.1 определятся формулами:

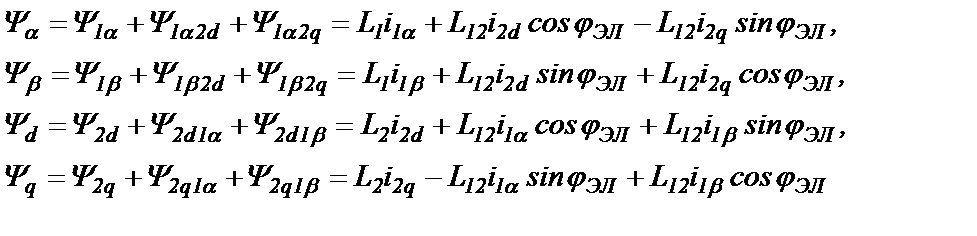(21.5)

Напряжения питания uα, uβ, ud и uq двухфазных обмоток изменяются с частотами трехфазного АД - в статоре с частотой ω1, в роторе с частотой ω2.

Преимущества двухфазной модели АД с раздельными осями статора (оси α-β) и ротора (оси d-q):

1) количество дифференциальных уравнений обмоток уменьшилось до 4-х (в трехфазной модели 6 уравнений);

2) количество слагаемых в выражениях полных потокосцеплений обмоток уменьшилось до 3-х (в трехфазной модели 6 слагаемых).

Недостаток только один: выражения потокосцеплений (21.5) являются нелинейными функциями, поэтому и дифференциальные уравнения (21.4) также нелинейные. Решить эти уравнения аналитически невозможно.

Устранить нелинейность в выражениях потокосцеплений и, следовательно, превратить дифференциальные уравнения АД в линейные можно путем:

1) замены обмоток в осях α-β, неподвижных относительно статора, и замены обмоток в осях d-q, неподвижных относительно ротора, на пары обмоток статора и ротора, которые неподвижны относительно осей u-v, вращающихся в пространстве с произвольной частотой;

2) изменением частоты напряжений, питающих обмотки статора и ротора в осях u-v.

Двухфазная модель с указанными свойствами приведена на рис.22.1. В исходном двухфазном АД с раздельными осями α-β и d-q:

- на статорную обмотку подаются напряжения uα и uβ с частотой ω1, в результате чего статором создается вращающееся магнитное поле с частотой вращения ω1;

- на роторную обмотку подаются напряжения ud и uq с частотой ω2=sω1, в результате чего в роторе создается вращающееся магнитное поле с частотой вращения sω1, а так ротор вращается с частотой ωЭЛ=ω1(1-s), то в пространстве поле ротора вращается с частотой ω2+ωЭЛ=ω1. Таким образом, поля статора и ротора вращаются в пространстве с одинаковой частотой ω1.

Если взять за основу синхронность вращения полей статора и ротора, то легко обосновать двухфазную модель АД в осях, общих для статора и ротора.

Пусть координатные оси u-v вращаются в пространстве с частотой ωК, и на этих осях расположены обмотки с витками w1u и w1v, заменяющие статор, и обмотки с витками w2u и w2v, заменяющие ротор. Для того, чтобы указанные пары обмоток создавали поля, вращающиеся в пространстве с частотой ω1, к ним нужно подвести напряжения u1u, u1v, u2u и u2v с частотой (ω1-ωК). Напряжения u1u и u1v должны быть сдвинуты между собой на 90о и также на 90о должны быть сдвинуты между собой напряжения u2u и u2v. Между напряжениями u1u и u2u сдвиг устанавливается в зависимости от требуемой величины вращающего момента АД.

Суммарные потокосцепления Ψ1u, Ψ1v, Ψ2u и Ψ2v всех четырех двухфазных обмоток с учетом построений на рис.22.1 определятся линейными относительно токов выражениями:

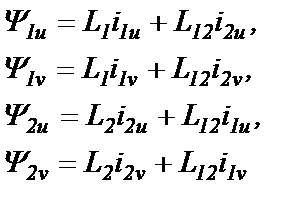(22.1)

Вывод дифференциальных уравнений обмоток в осях u-v производится ниже в теме 23.

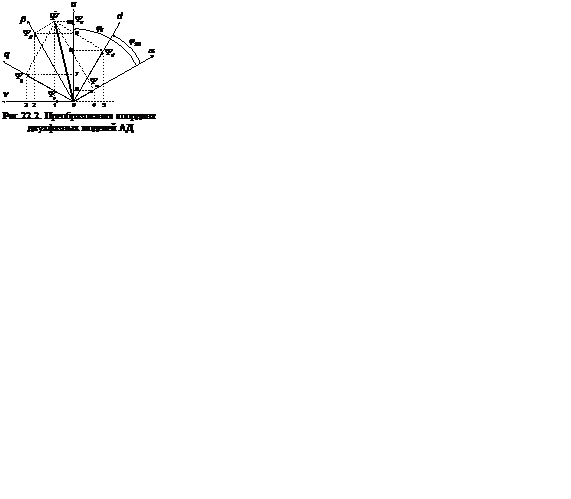
Если аналитически рассчитаны напряжения, токи и потокосцепления статора и ротора в осях u-v, то возникает задача перехода к этим же величинам, но в осях α-β статора и осях d-q ротора и наоборот. Такой пересчет выполняется с использованием формул преобразования координат, для вывода которых используем построения, приведенные на рис.22.2.

Вывод формул преобразования (u-v) ← (α-β)

Из чертежа следует равенство для проекций на оси u и v:

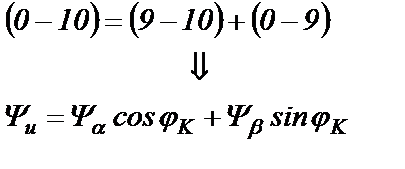
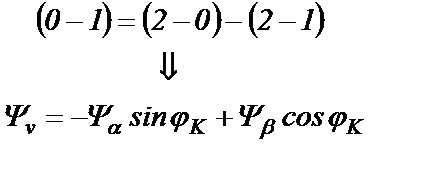(22.2)

В матричном виде

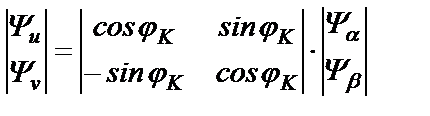(22.3)

Вывод формул преобразования (α-β) ← (u-v)

Решив (22.3) относительно Ψα и Ψβ , получим

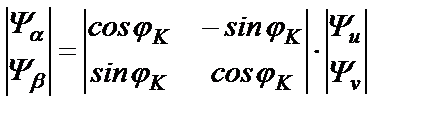(22.4)

Вывод формул преобразования (u-v) ← (d-q) и (d-q) ← (u-v)

Из чертежа следует равенство для проекций на ось u:

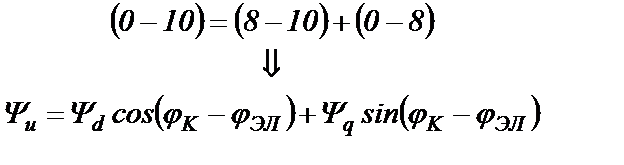
и на ось v: (22.5)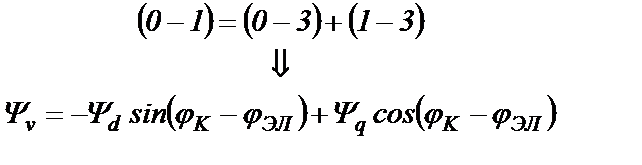

В матричном виде 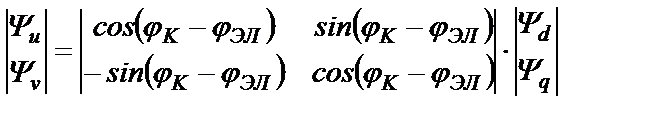(22.6)

и обратно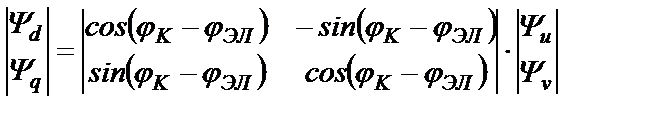

Асинхронно вентильный каскад электропривода, содержащего АД с фазным ротором. Как с помощью инвертора напряжения ведомого сетью регулируется частота вращения АД? Почему к.п.д. асинхронно-вентильного каскада выше к.п.д. электропривода с реостатами в цепи ротора АД?

В регулировочных режимах в сопротивлении RP выделятся тепло. Мощность тепловыделений равна произведению напряжения URP на сопротивлении RP и тока IRP через него (что и уменьшает КПД). Эту мощность можно с помощью инвертора напряжения преобразовать в мощность переменного тока и отдать (рекуперировать) ее в сеть. Наиболее простое решение рекуперации энергии достигается на ведомом сетью инверторе напряжения.

Схема асинхронно-вентильного каскада (АВК) содержит (рис.19.1) АД, в цепи фазного ротора которого имеется неуправляемый выпрямитель, и ведомый сетью инвертор напряжения на базе управляемого выпрямителя.

К инвертору от выпрямителя ВКД (вентильного комплекта двигателя) подведена э.д.с., пропорциональная скольжению s АД. Угол опережения β инвертора выбирается таким, чтобы между напряжениями ВКД и ВКИ соблюдалось соотношение 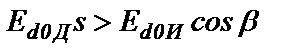. Инвертор, состоящий из вентильного комплекта ВКИ и согласующего трансформатора Тр, потребляет мощность постоянного тока 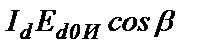и эта мощность, но уже на переменном токе, подведена к нижним (по схеме) обмоткам трехфазного трансформатора и затем трансформируется в обмотки, подсоединенные к сети. Таким образом, мощность цепи ротора АД, которая в схемах на рис.18.2 и рис.18.3 рассеивалась в виде тепловой мощности в регулировочном резисторе RР, в схеме АВК отдается в сеть. К.п.д. АВК во всем диапазоне частот вращения АД поддерживается на максимально достижимом уровне – порядка 0,85…0,95.

САР частоты вращения АД на базе АВК может быть вполне удовлетворительным даже, если она выполнена по схеме разомкнутого типа, так как механические характеристики схемы АВК близки к характеристикам частотного управления, приведенными на рис.13.3в, что доказывается ниже.

У АД, не используемого в АВК, существует только одно значение скольжения холостого хода на естественной характеристике sXXе=0, при котором вращающий момент АД нулевой. У АД, используемого в АВК, на искусственных механических характеристиках существует бесконечно много значений скольжения холостого хода sXXβ, при котором вращающий момент АД нулевой, и эти скольжения зависят от угла опережения β инвертора. Действительно, вращающий момент М АД обращается в ноль, если во всех его роторных обмотках токи нулевые и, следовательно, нулевой ток Id (рис.19.1). Ток Id согласно рис.19.1 равен 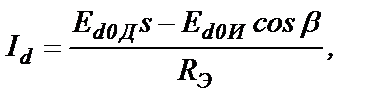(19.1)

где RЭ – эквивалентное сопротивление цепи протекания тока Id.

Ток Id обращается в ноль согласно (19.1) при скольжении 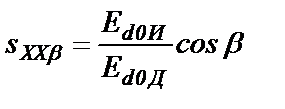(19.2)

Только при β=90О скольжение sXXβ=0 и совпадает с sXXе=0 для АД без АВК.

Жесткость искусственных механических характеристик, как показывают расчеты, уменьшается при увеличении скольжения sXXβ. Зная скольжения sXXβ холостого хода естественной или искусственных механических характеристик, можно рассчитать частоты вращения холостого ωХХ хода для этих характеристик по формуле

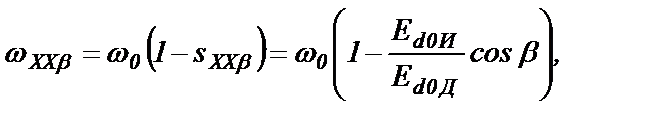(19.3)

где ω0 - частота вращения магнитного поля статора.

Механические характеристики АД, включенного в схему АВК, приведены на рис.19.2. Из них следует, что для повышения частоты вращения АД в схеме разомкнутого типа нужно увеличить угол опережения β. С увеличением β значение входного напряжения инвертора 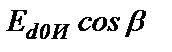уменьшится и при неизменном значении выходного напряжения 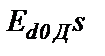ВКД ток Id согласно (19.1) увеличится, увеличится далее вращающий момент двигателя и частота вращения будет возрастать. Значение напряжение на кольцах ротора и, следовательно, 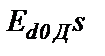будут уменьшаться.

Для уменьшения частоты вращения угол β нужно уменьшать, увеличив тем самым, входное напряжение 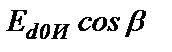ВКИ. Ток Id уменьшится, уменьшится вращающий момент М и частота вращения АД будет понижаться.

Более качественное регулирование частоты вращения АД с любой жесткостью механических характеристик АЭП и другими заданными показателями качества, например, показателями качества модального управления, может быть достигнуто при включении схемы АВК (рис.19.1) в контур регулирования скорости. Схема САР частоты вращения с использованием АВК приведена на рис.19.3. Она подобна схеме с рис.18.3 с тем отличием, что СИФУ управляет тиристорами вентильного комплекта ВКИ инвертора АВК.

Скалярные системы автоматического управления асинхронными двигателями базируются только на прямом учете параметров механических переходных процессов, но они не учитывают в полном объеме электрические и электромеханические процессы. Для мощных АД, имеющих значительную электрическую инерцию, а также для электроприводов, к которым предъявляются высокие требования к динамическим процессам, сложно реализовать качественный АЭП без учета электрических переходных процессов. Такие требования могут быть учтены, если использовать полные дифференциальные уравнения обмоток АД, что реализовано в системах векторного управления АД.