Пересечение поверхности вращения плоскостью
Форма сечения поверхности вращения плоскостью зависит от угла наклона секущей плоскости к оси вращения поверхности.
Если секущая плоскость:
1) перпендикулярна оси вращения, сечение – окружность;
2) наклонена к оси и пересекает все образующие – эллипс;
3) параллельна одной образующей – парабола;
4) параллельна двум образующим – гипербола;
5) проходит через вершину – две пересекающиеся прямые;
6) касается поверхности – прямая.
Вся совокупность этих линий может быть получена при пересечении конуса плоскостью. Поэтому их называют коническими сечениями, или кониками.
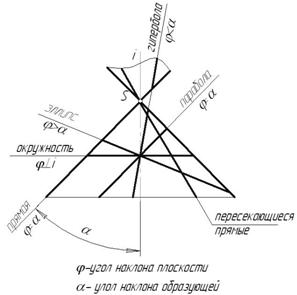
Рис. 6.14
Для построения линии пересечения необходимо найти общие точки поверхности и заданной плоскости. Для определения этих точек необходимо ввести дополнительные секущие плоскости, которые дают наиболее простые линии сечения – окружности или ломаные прямые.
Построение линии сечения начинают с нахождения характерных точек сечения, к которым относятся:
1) высшая и низшая точки;
2) крайняя левая и крайняя правая точки, в которых проекции линии сечения касаются очерковых образующих (точки, лежащие на границе видимости);
3) ближайшая и наиболее удаленная точки сечения.
Пример: Определить линию сечения конуса плоскостью общего положения Q(hÇf). Построить развертку нижней отсеченной поверхности конуса.
Анализ формы линии пересечения
Заданная плоскость пересекает только боковую поверхность конуса, следовательно, линией сечения q является эллипс.
Характерные точки линии пересечения:
1) Высшая и низшая точки сечения (А, В) определяют большую ось эллипса и лежат на линии наибольшего наклона плоскости 
к плоскости основания конуса. Эти точки определяются с помощью дополнительной плоскости 
.
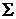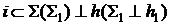
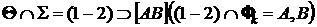
О – центр эллипса
2) Малая ось эллипса (С, D) перпендикулярна к линии наибольшего наклона (большой оси), т.е. лежит на горизонтали плоскости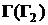 
.
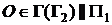
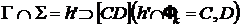
3) Точки границы видимости (E, F) сечения на 
лежат в плоскости 
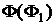, делящей конус на видимую и невидимую части по отношению к фронтальной плоскости проекций.
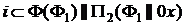
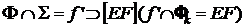
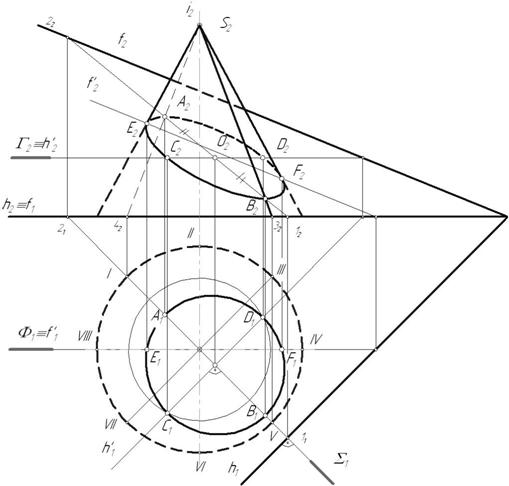
Рис. 6.15
Развертка
Полная развертка боковой поверхности конуса представляет собой угол кругового сектора. Ее можно построить двумя способами:
1. Нахождение угла кругового сектора.
Рис. 6.16
где d – диаметр окружности основания конуса,
l – длина образующей.
2. Способ малых хорд.
Графическое построение величины 
осуществляется способом малых хорд, при котором окружность основания конуса делится на 8 или 12 равных частей и полученная длина дуги приравнивается ее хорде.
Разрывать отсеченную боковую поверхность следует по наиболее короткой или длинной образующей, так чтобы развертка представляла собой симметричную фигуру и была единым целым.
Рис. 6.17
Пересечение поверхностей
Пересечение многогранников
Многогранники пересекаются по замкнутым пространственным ломаным линиям, которые могут быть найдены следующим образом:
1. Способ ребер. Находятся точки пересечения ребер одного многогранника с гранями другого.
2. Способ граней. Определяются отрезки прямых, по которым грани одного многогранника пересекаются с гранями другого.
Пример: Построить линию пересечения двух трехгранных призм, одна из которых проецирующая.
В результате пересечения заданных многогранников получается ломаная пространственная линии. Она соединяет соответствующие точки пересечения ребер одного многогранника с гранями другого. Так как одна из призм проецирующая относительно горизонтальной плоскости проекций, горизонтальная проекция линии пересечения совпадает с горизонтальным очерком этой призмы. Искомые точки сечения можно получить, решая задачу на пересечение прямой (ребра) с плоскостью (гранью).
, 
.
, 
.
Для построения точек пересечения ребра b с гранями призмы, используется горизонтально-проецирующая плоскость .
.
.
Рис. 6.18
Для определения видимости линии сечения строится диаграмма, на которой схематично в произвольных размерах изображаются грани заданных призм. Знаками ²+² и ²-² отмечается видимость граней многогранников. На соответствующих гранях и ребрах наносятся точки сечения, и соединяют их с учетом видимости. Видимыми считаются те звенья линии пересечения, которые лежат на видимых гранях обоих многогранников.
Лекция 11