Графический метод решения задач линейного программирования в случае двух переменных.

См. лекцию 3 (стр. 3-5) МатМетоды в экономике. Лекция 3 – графический метод

20. Постановка транспортной задачи. Построение первоначального плана перевозок с помощью методов северо-западного угла и наименьшей стоимости.

МатМетоды в экономике. Лекция 7 (конец)– постановка транспортной задачи.

Правильность составленного плана легко проверить:

1. подсчитав суммы чисел, стоящих в заполненных клетках по строкам и столбцам. Должна ровняться запасам/потребностям в закрытой задаче.

2. в таблице перевозок, представляющей опорный план, мы имеем 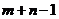заполненных и 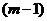* 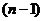пустых клеток.

Построение первоначального плана перевозок с помощью методов северо-западного угла.

При этом методе на каждом шаге построения первого опорного плана заполняется левая верхняя клетка (северо-западный угол) оставшейся части таблицы. При таком методе заполнение таблицы начинается с клетки неизвестного 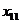и заканчивается в клетке неизвестного 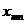, т. е. идет как бы по диагонали таблицы перевозок.

Заполнение таблицы начинается с ее северо-западного угла, т. е. клетки с неизвестным 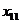. Первая база 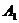может полностью удовлетворить потребность первого заказчика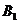 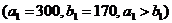. Полагая 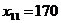, вписываем это значение в клетку 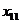и исключаем из рассмотрения первый столбец. На базе 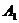остается измененный запас 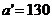. В оставшейся новой таблице с тремя строками 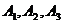и четырьмя столбцами 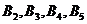; северо-западным углом будет клетка для неизвестного 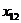. Первая база с запасом 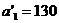может полностью удовлетворить потребность второго заказчика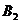 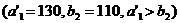. Полагаем 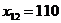, вписываем это значение в клетку 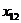и исключаем из рассмотрения второй столбец. На базе 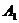остается новый остаток (запас) 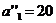. В оставшейся новой таблице с тремя строками 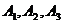и тремя столбцами 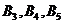северо-западным углом будет клетка для неизвестного 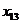. Теперь третий заказчик 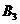может принять весь запас с базы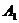 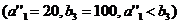. Полагаем 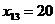, вписываем это значение в клетку 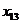и исключаем из рассмотрения первую строку. У заказчика из 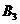осталась еще не удовлетворенной потребность .

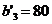Теперь переходим к заполнению клетки для неизвестного 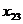и т.д.

Через шесть шагов у нас останется одна база 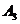с запасом груза (остатком от предыдущего шага) 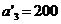и один пункт 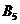с потребностью 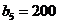. Соответственно этому имеется одна свободная клетка, которую и заполняем, положив 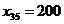. План составлен. Базис образован неизвестными .

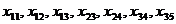Правильность составленного плана легко проверить:

1. подсчитав суммы чисел, стоящих в заполненных клетках по строкам и столбцам. Должна ровняться запасам/потребностям в закрытой задаче.

2. в таблице перевозок, представляющей опорный план, мы имеем заполненных и * пустых клеток.

Общий объем перевозок в тонно-километрах для этого плана составит

.

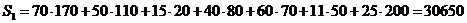Для получения оптимального опорного плана необходимо перебрать все возможные варианты и из них выбрать вариант перевозок с наименьшим S*.

Пункты Отправления	Пункты назначения	Запасы
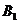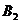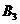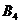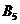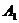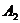Потребности

Метод наименьшей стоимости.

При этом методе на каждом шаге построения опорного плана первою заполняется та клетка оставшейся части таблицы, которая имеет наименьший тариф. Если такая клетка не единственная, то заполняется любая из них.

Пример:

Пункты отправления	Пункты назначения	Запасы
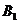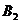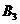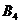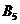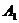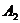Потребности

В данном случае заполнение таблицы начинается с клетки для неизвестного 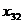, для которого мы имеем значение 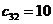, наименьше из всех значений 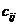. Эта клетка находится на пересечении третьей строки и второго столбца, соответствующим третьей базе 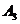и второму заказчику 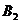. Третья база 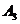может полностью удовлетворить потребность второго заказчика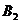 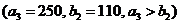. Полагая 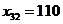, вписываем это значение в клетку 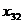и исключаем из рассмотрения второй столбец. На базе 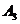остается изменённый запас 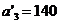. В оставшейся новой таблице с тремя строками 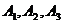и четырьмя столбцами 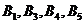клеткой с наименьшим значением 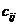клетка, где 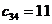. Заполняем описанным выше способом эту клетку и аналогично заполняем следующие клетки. В результате оказываются заполненными (в приведенной последовательности) следующие клетки:

.

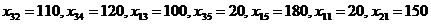На пятом шаге клеток с наименьшими значениями 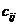оказалось две 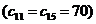. Мы заполнили клетку для 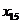, положив 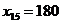. Можно было выбрать для заполнения другую клетку, положив 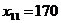, что приведет в результате к другому опорному плану. Общий объем перевозок в тонно-километрах для этого плана составит

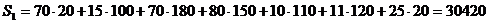
Замечание. В диагональном методе не учитываются величины тарифов, в методе же наименьшей стоимости эти величины учитываются, и часто последний метод приводит к плану с меньшими общими затратами (что и имеет место в нашем примере), хотя это и не обязательно.