Классическое определение вероятности. Геометрические вероятности. Операции над событиями. Вероятность суммы двух событий.

Самаров- ТЕОРИЯ ВЕРОЯТНОСТЕЙ.pdf - стр. 3 – 5

+

http://www.toehelp.ru/theory/ter_ver/

Классическое определение вероятности. Пусть события E1,E2, ..., En в одном опыте образуют полную группу равновероятных и попарно несовместных событий (к примеру бросание игральной кости). Будем называть их исходами испытания. Предположим, что событию A благоприятствуют M исходов испытания. Тогда вероятностью события A в данном опыте называют отношение M/N. Итак, мы приходим к следующему определению:

Вероятностью P(A) события в определенном опыте называется отношение числа M исходов опыта, благоприятствующих событию A, к общему числу N возможных исходов опыта, образующих полную группу равновероятных попарно несовместных событий:

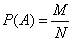
Это определение вероятности часто называют классическим. Можно сказать, что классическое определение удовлетворяет аксиомам вероятности.

Событие A может появиться k раз в n испытаниях в различных комбинациях, число которых равно количеству сочетаний из n элементов по k. Это количество сочетаний находится по формуле: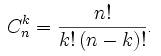

Геометрические вероятности. Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности — вероятности попадания точки в область (отрезок, часть плоскости и т. д.).

Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Это означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка L, вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L. В этих предположениях вероятность попадания точки на отрезок l определяется равенством

Р = Длина l / Длина L.

Операции над событиями.

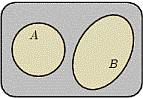
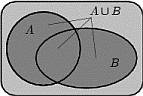
1. Объединением 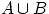(или суммой A+B) двух событий A и В называется событие С, заключающееся в том, что произойдет по крайней мере одно из событий A или В. Это событие обозначается так: С=А+В. Объединением нескольких событий называется событие, состоящее в появлении по крайней мере одного из них. Запись D=A+B+C означает, что событие D есть объединение событий A, В и С.

Объединением событий A и B называется событие, состоящее в том, что произошло либо A, либо B, либо оба события одновременно.

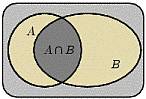
2. Совмещением 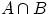(или произведением A*B) двух событий A и В называется событие, состоящее в совместном наступлении как события A, так и события В. Это событие будем обозначать АВ или ВА.

3. Разностью (дополнение 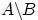) событий A-B называется событие C, состоящее из всех элементарных событий, входящих в A, но не входящих в B.

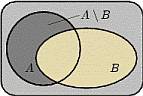
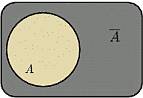
4. Противоположным к событию A называется событие 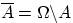, состоящее в том, что событие A в результате эксперимента не произошло. Т.е. множество 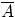состоит из элементарных исходов, не входящих в A.

5. События A и B называют несовместными, если 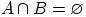, т.е. совмещение (произведение) А и В равно пустому множеству (нулю), они не могут произойти одновременно.