Если строки (столбцы) определителя пропорциональны, то он равен нулю. Определитель с нулевой строкой (столбцом) равен нулю.
2. ВЫПОЛНИТЬ ДЕЙСТВИЯ НАД МАТРИЦАМИ:
Даны матрицы А и В. Найти матрицу С.
| N варианта | Матрица А | Матрица В | Матрица С |
| 2.1 | 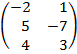 | 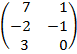 | С=2АТ 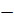 ВТ ВТ |
| 2.2 | 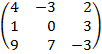 | 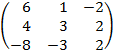 | С=ЕА 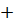 ВТ ВТ |
| 2.3 | 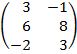 | 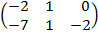 | С=АТ 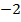 ВТ ВТ |
| 2.4 | 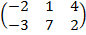 | 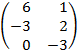 | С=2АТ 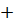 ВТ ВТ |
| 2.5 | 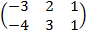 | 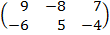 | С=АТ 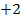 ВТ ВТ |
| 2.6 | 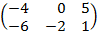 | 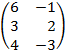 | С=3В 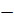 АТ АТ |
| 2.7 | 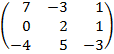 | 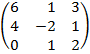 | С=А 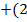 В)Т В)Т |
| 2.8 | 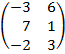 | 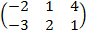 | С=АТ 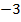 В В |
| 2.9 | 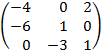 | 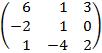 | С=2А 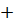 В В |
| 2.10 | 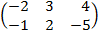 | 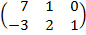 | С=2А 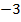 В В |
| 2.11 | 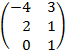 | 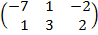 | С=3А 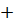 ВТ ВТ |
| 2.12 | 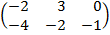 | 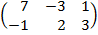 | С=3А 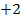 В В |
| 2.13 | 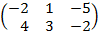 | 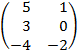 | С=2В  АТ АТ |
| 2.14 | 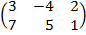 | 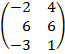 | С=А 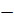 ВТ ВТ |
| 2.15 | 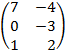 | 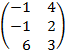 | С=3В 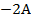 |
| 2.16 | 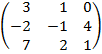 | 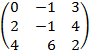 | С=(2В)Т 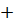 А А |
| 2.17 | 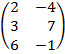 | 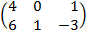 | С=2А 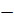 ВТ ВТ |
| 2.18 | 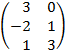 | 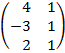 | С=АТ 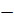 ВТ ВТ |
| 2.19 | 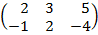 | 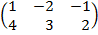 | С=2А 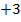 В В |
| 2.20 | 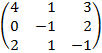 | 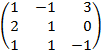 | С=(3А)Т 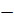 В В |
| 2.21 | 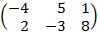 | 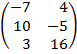 | С=В 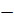 2АТ 2АТ |
| 2.22 | 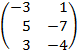 | 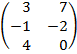 | С=2ВТ 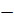 (2А)Т (2А)Т |
| 2.23 | 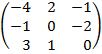 | 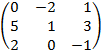 | С=(2А)Т  В В |
| 2.24 | 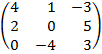 | 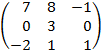 | С=3В  2АТ 2АТ |
| 2.25 | 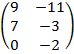 | 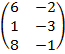 | С=А 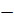 3В 3В |
ОБРАЗЕЦ ВЫПОЛНЕНИЯ 0-го варианта 2-го задания:
2. Действия над матрицами. Даны матрицы А и В. Найти матрицу С.
| N варианта | Матрица А | Матрица В | Матрица С |
| 2.0 |  | 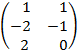 | С=2АТ 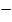 ВТ ВТ |
С=2АТ 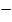 ВТ
ВТ
Для вычисления данного выражения необходимо транспонировать заданные матрицы, т.е. поменять строки и столбцы местами:
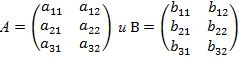 , т.е.
, т.е. 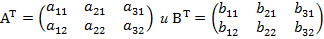 , затем умножить соответствующую матрицу на коэффициент, заданный в выражении, и произвести вычисления:
, затем умножить соответствующую матрицу на коэффициент, заданный в выражении, и произвести вычисления:
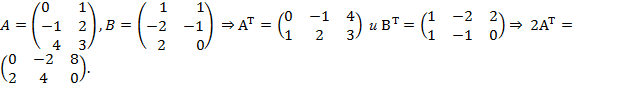
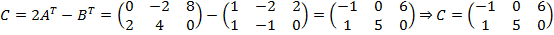 .
.
Ответ: 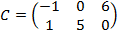
3.ВЫЧИСЛИТЬ ПРОИЗВЕДЕНИЕ МАТРИЦ А∙В. Проверить, существует ли произведение В∙А, если существует – вычислить.
| N варианта | Матрица А | Матрица В |
| 3.1 | 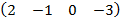 | 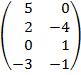 |
| 3.2 | 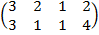 | 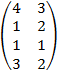 |
| 3.3 | 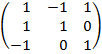 | 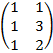 |
| 3.4 | 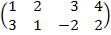 | 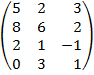 |
| 3.5 | 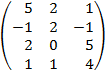 | 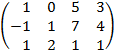 |
| 3.6 | 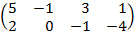 | 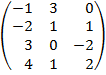 |
| 3.7 | 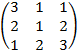 | 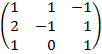 |
| 3.8 | 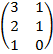 | 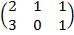 |
| 3.9 | 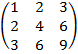 | 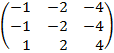 |
| 3.10 | 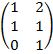 | 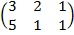 |
| 3.11 | 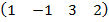 | 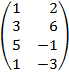 |
| 3.12 | 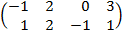 | 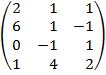 |
| 3.13 | 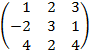 | 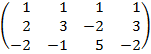 |
| 3.14 | 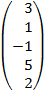 |  |
| 3.15 | 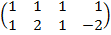 | 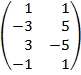 |
| 3.16 | 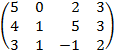 | 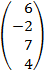 |
| 3.17 | 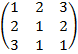 | 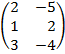 |
| 3.18 | 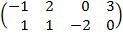 | 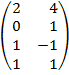 |
| 3.19 | 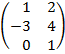 | 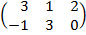 |
| 3.20 | 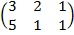 | 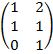 |
| 3.21 | 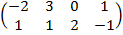 | 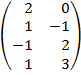 |
| 3.22 | 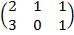 | 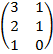 |
| 3.23 | 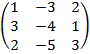 | 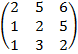 |
| 3.24 | 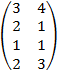 | 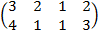 |
| 3.25 | 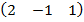 | 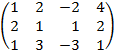 |
ОБРАЗЕЦ ВЫПОЛНЕНИЯ 0-го варианта 3-го задания:
3. Вычислить произведение матриц А∙В. Проверить, существует ли произведение В∙А.
| N варианта | Матрица А | Матрица В |
| 3.0 | 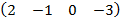 | 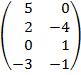 |
Условием существования произведения матриц является их согласованность», т.е. количество столбцов в первой матрице должно быть равно количеству строк во второй матрице. Матрица А имеет 1 строку и 4 столбца. матрица В – 4 строки и 2 столбца. Следовательно, произведение А∙В возможно, а В∙А посчитать невозможно:
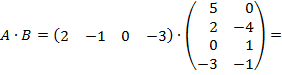
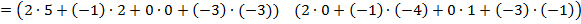
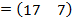
Ответ: 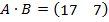
4. НАЙТИ ОБРАТНУЮ МАТРИЦУ ДЛЯ МАТРИЦЫ А. Сделать проверку.
| N варианта | Матрица А |
| 4. 1 | 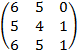 |
| 4. 2 | 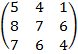 |
| 4. 3 | 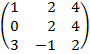 |
| 4. 4 | 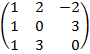 |
| 4. 5 | 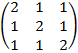 |
| 4. 6 | 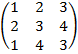 |
| 4. 7 | 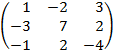 |
| 4. 8 | 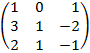 |
| 4. 9 | 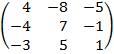 |
| 4. 10 | 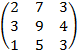 |
| 4. 11 | 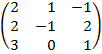 |
| 4. 12 | 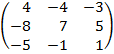 |
| 4. 13 | 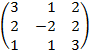 |
| 4. 14 | 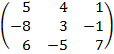 |
| 4. 15 | 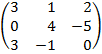 |
| 4. 16 | 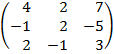 |
| 4. 17 | 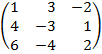 |
| 4. 18 | 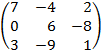 |
| 4. 19 | 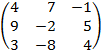 |
| 4. 20 | 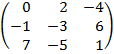 |
| 4. 21 | 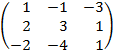 |
| 4. 22 | 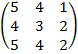 |
| 4. 23 | 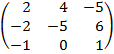 |
| 4. 24 | 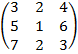 |
| 4. 25 | 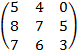 |
ОБРАЗЕЦ ВЫПОЛНЕНИЯ 0-го варианта 4-го задания:
4. Найти обратную матрицу для матрицы А. Сделать проверку.
| N варианта | Матрица А |
| 4.0 | 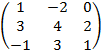 |
Найдите обратную матрицу для матрицы 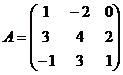 .
.
Решение. Находим определитель
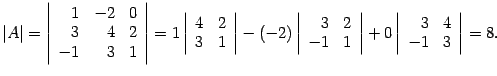
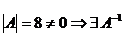 , т.е. матрица
, т.е. матрица 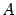 - невырожденная, и обратная для нее существует.
- невырожденная, и обратная для нее существует.
Находим алгебраические дополнения:
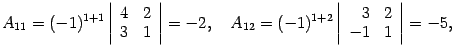
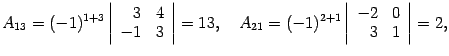
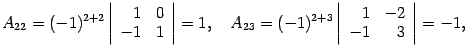
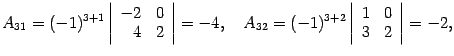
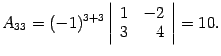 Составляем обратную матрицу, размещая найденные алгебраические дополнения так, чтобы первый индекс соответствовал столбцу, а второй – строке. Полученная матрица и служит ответом.
Составляем обратную матрицу, размещая найденные алгебраические дополнения так, чтобы первый индекс соответствовал столбцу, а второй – строке. Полученная матрица и служит ответом.
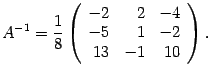
Для проверки правильности нахождения обратной матрицы, необходимо произвести умножение матрицы А на матрицу  . Их произведение должно быть равно матрице
. Их произведение должно быть равно матрице 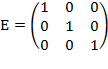 . В противном случае – обратная матрица найдена ошибочно, необходимо переделать задание.
. В противном случае – обратная матрица найдена ошибочно, необходимо переделать задание.
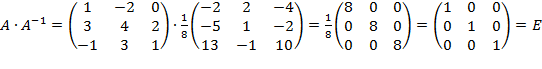 .
.
5. РЕШИТЬ МАТРИЧНОЕ УРАВНЕНИЕ:
| N варианта | Матричное уравнение |
| 5. 1 | 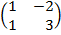 ∙Х = ∙Х = 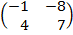 |
| 5. 2 | 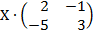 = = 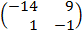 |
| 5. 3 | 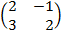 ∙Х = ∙Х = 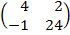 |
| 5. 4 | 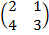 ∙Х = ∙Х = 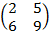 |
| 5. 5 | 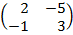 ∙Х = ∙Х = 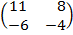 |
| 5. 6 | 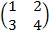 ∙Х = ∙Х = 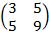 |
| 5. 7 | 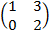 ∙Х = ∙Х = 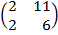 |
| 5. 8 | 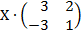 = = 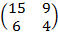 |
| 5. 9 | 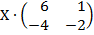 = = 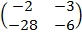 |
| 5. 10 | 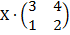 = = 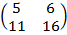 |
| 5. 11 | 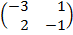 ∙Х = ∙Х = 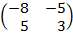 |
| 5. 12 | 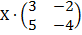 = = 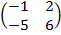 |
| 5. 13 | 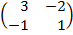 ∙Х = ∙Х = 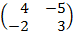 |
| 5. 14 | 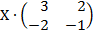 = = 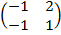 |
| 5. 15 | 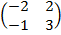 ∙Х = ∙Х = 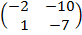 |
| 5. 16 | 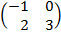 ∙Х = ∙Х = 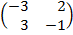 |
| 5. 17 | 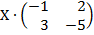 = = 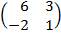 |
| 5. 18 | 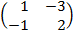 ∙Х = ∙Х = 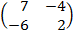 |
| 5. 19 | 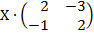 = = 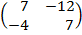 |
| 5. 20 | 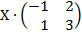 = = 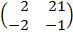 |
| 5. 21 | 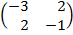 ∙Х = ∙Х = 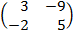 |
| 5. 22 | 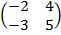 ∙Х = ∙Х = 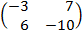 |
| 5. 23 | 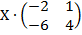 = = 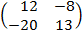 |
| 5. 24 | 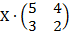 = = 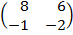 |
| 5. 25 | 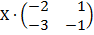 = = 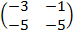 |
ОБРАЗЕЦ ВЫПОЛНЕНИЯ 0-го варианта 5-го задания:
5. Решить матричное уравнение:
| N варианта | Матричное уравнение |
| 5.0 | 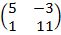 ∙Х = ∙Х = 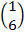 |
Матричные уравнения могут иметь вид:
АХ = В, ХА = В, АХВ = С, где А, В, С — задаваемые матрицы, Х- искомая матрица.
Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы.
Например, чтобы найти матрицу 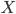 из уравнения
из уравнения 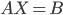 , необходимо умножить это уравнение на
, необходимо умножить это уравнение на 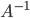 слева.
слева.
Тогда: 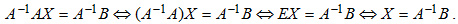
Следовательно, чтобы найти решение 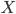 уравнения
уравнения 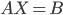 , нужно найти обратную матрицу
, нужно найти обратную матрицу 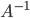 и умножить ее на матрицу
и умножить ее на матрицу 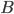 , стоящие в правой части уравнения.
, стоящие в правой части уравнения.
Аналогично решаются другие уравнения.
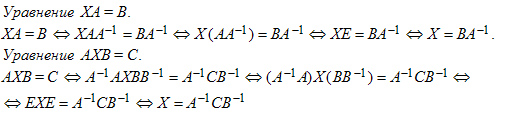
Дано уравнение 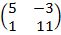 ∙Х =
∙Х = 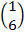 . Для решения данного уравнения необходимо найти обратную матрицу матрице
. Для решения данного уравнения необходимо найти обратную матрицу матрице 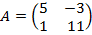 ;
;
1) первоначально найдем определитель матрицы А 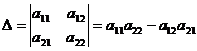 =55+3=58;
=55+3=58;
2) найдем элементы обратной матрицы:
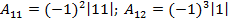
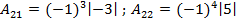 ;
;
3) найдем обратную матрицу: 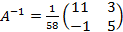 ;
;
4) найдем матрицу X по формуле 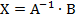 как произведение 2-х матриц:
как произведение 2-х матриц:
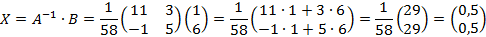
Ответ: 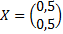
VI. ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ ПО ТЕМЕ:
- Что называется матрицей?
- Что называется матрицей-строкой, матрицей столбцом?
- Какие матрицы называются прямоугольными, квадратными?
- Какие матрицы называются равными?
- Что называется главной диагональю матрицы?
- Какая матрица называется диагональной?
- Какая матрица называется единичной?
- Какая матрица называется треугольной?
- Что значит транспонировать матрицу?
- Что называется суммой матриц?
- Что называется произведением матрицы на число?
- Как найти произведение двух матриц?
- В чем состоит обязательное условие существования произведения матриц?
- Что называется определителем матрицы?
- Как вычислить определитель третьего порядка по схеме треугольников?
- Что называется минором?
- Что называется алгебраическим дополнением элемента определителя?
- Как разложить определитель по элементам столбца или строки?
- Перечислите свойства определителя.
- Какая матрица называется невырожденной?
- Какая матрица называется обратной по отношению к данной?
- Каков алгоритм нахождения обратной матрицы?
VIII. СПИСОК ЛИТЕРАТУРЫ.
Основные источники:
1. Дадаян А.А. Математика: учебник для студ. учреждений СПО: учебник. - 3-e изд. - М.: Форум, 2013.
2. Балдин К.В. Краткий курс высшей математики: учебное пособие для вузов. - М. : Дашков и К°, 2013.
3. Березина Н.А. Высшая математика: учебное пособие для высших и средних учебных заведений. - Саратов: Научная книга, 2012.
4. Березина Н.А. Математика: учебное пособие для высших и средних учебных заведений/ Н.А. Березина, Е.Л. Максина. - М.: РИОР: Инфра-М, 2013.
5. Григорьев В.П. Математика: учебник для студ. учреждений СПО/ В.П.Григорьев, С.В.Иволгина; под ред. В.А.Гусева. - М.: Академия, 2014.
6. Майоровская С. В. Элементы высшей математики: учебник для студ. учреждений СПО/ С. В.Майоровская, О.Н.Поддубная, Л.В. Станишевская.- Мн.: Вышэйшая школа, 2010.
7. Шипачёв В.С. Высшая математика: учебник. - М.: ИНФРА-М, 2015.
8. Шипачёв В.С. Задачник по высшей математике: учебное пособие. - 10-e изд., стер. - М.: ИНФРА-М, 2015.
Дополнительные источники:
1. Балдин К.В. Высшая математика: учебное пособие для вузов.- М.: Флинта, 2010.
2. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи.- М.: Гардарики, 2002.
3. Богомолов Н.В. Практические занятия по математике: учебное пособие для средних проф. учеб. заведений.-М.: Высш. шк., 2009.
4. Григорьев В.П. Элементы высшей математики: учебник для студ. учреждений СПО/ В.П.Григорьев, Ю.А.Дубинский.—М.: Академия, 2009.
5. Б е к л е м и ш е в Д. В. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1971.
6. Е ф и м о в Н. В. Краткий курс аналитической геометрии. −М.: Наука, 1972.
7. К а г а н М. Л., С а м о х и н М. В. Алгебра и геометрия. –М.: Стройиздат, 2003.
8. К л е т е н и к Д. В. Сборник задач по аналитической геометрии. – М.: Наука, 1967.
Интернет-ресурсы:
1. Exponenta.ru: образовательный математический сайт [Электронный ресурс].- Режим доступа: http://www.exponenta.ru/, свободный.
2. MATH24.ru. Математический анализ: образовательный сайт. 2009-2013. [Электронный ресурс].- Режим доступа: http://www.math24.ru/, свободный.
3. Математика [Электронный ресурс]: интерактивный обучающий курс/ Институт менеджмента, маркетинга и финансов. - Режим доступа: http://math.immf.ru/, свободный.
