Понятие аналитической функции компл. переменного.
Аналитическое продолжение вдоль цепочки областей.
Пусть даны две области 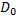 ,
, 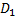 , и пусть их пересечение
, и пусть их пересечение 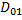 не пусто и является областью (рис.53). Пусть ф.
не пусто и является областью (рис.53). Пусть ф. 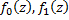 регулярны в областях
регулярны в областях 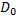 ,
, 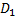 соответственно, и пусть эти ф. совпадают в области
соответственно, и пусть эти ф. совпадают в области 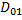 , т.е.
, т.е. 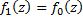 ,
, 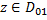 . Тогда ф.
. Тогда ф. 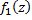 называется непосредственным аналитическим продолжением ф.
называется непосредственным аналитическим продолжением ф. 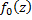 из области
из области 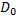 в область
в область 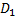 .
.

Всё аналогично и в случае 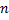 областей (рис.54). Ф.
областей (рис.54). Ф. 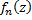 называется аналитическим продолжением ф.
называется аналитическим продолжением ф. 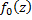 вдоль цепочки областей
вдоль цепочки областей 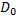 ,
, 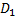 ,
, 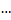 ,
, 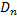 . Это продолжение единственно. Полученный набор регулярных ф.
. Это продолжение единственно. Полученный набор регулярных ф. 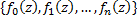 определяет некоторую ф.
определяет некоторую ф. 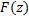 . Её значения определяются формулой:
. Её значения определяются формулой: 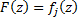 ,
, 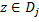 . Заметим, что
. Заметим, что 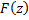 может оказаться неоднозначной, т.е.
может оказаться неоднозначной, т.е. 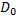 может пересечься с
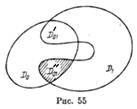
может пересечься с 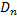 и цепочка областей замкнётся (Такое возможно даже на первом шаге! рис.55).
и цепочка областей замкнётся (Такое возможно даже на первом шаге! рис.55).
Аналитическое продолжение вдоль кривой.
Элементом в т. 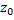 будем называть ф.
будем называть ф. 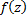 , регулярную в некоторой окрестности этой т.
, регулярную в некоторой окрестности этой т.
Определение: Пусть на кривой 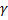 задана непрерывная ф.
задана непрерывная ф. 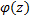 , в каждой т.
, в каждой т. 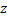 кривой
кривой 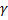 задан элемент
задан элемент 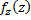 и этот элемент совпадает с
и этот элемент совпадает с 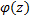 на некоторой дуге кривой
на некоторой дуге кривой 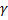 , содержащей т.
, содержащей т. 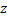 .
.
Тогда элемент 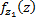 в конечной т.
в конечной т. 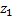 кривой
кривой 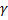 называется аналитическим продолжением вдоль кривой
называется аналитическим продолжением вдоль кривой 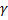 элемента
элемента 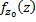 , заданного в нач. т.
, заданного в нач. т. 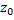 кривой
кривой 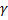 .
.
Определение аналитической функции.
Пусть в т. 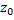 задан элемент
задан элемент 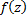 . Продолжим его аналитически по всем кривым с началом в т.
. Продолжим его аналитически по всем кривым с началом в т. 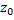 , по которым такое продолжение возможно; полученное множество элементов называется аналитической функцией, порождённой элементом
, по которым такое продолжение возможно; полученное множество элементов называется аналитической функцией, порождённой элементом 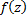 . Множество всех таких кривых называется множеством допустимых кривых.
. Множество всех таких кривых называется множеством допустимых кривых.
Точки и линии ветвления.
Риманова поверхность.
Рассмотрим случай неоднозначности продолжения (рис.55). Пусть ф. 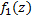 и
и 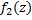 тождественно совпадают лишь на области
тождественно совпадают лишь на области 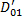 пересечения областей
пересечения областей 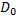 и
и 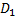 . Рассмотрим область
. Рассмотрим область 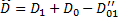 , где
, где 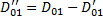 – та часть пересечения
– та часть пересечения 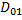 в которой ф.
в которой ф. 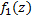 и
и 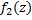 различны.
различны.
В области 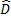 определена единственная аналитическая ф.
определена единственная аналитическая ф. 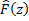 , являющаяся аналитическим продолжением
, являющаяся аналитическим продолжением 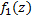 , заданной в области
, заданной в области 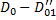 на область
на область 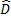 . Эта ф. тождественно совпадает с ф.
. Эта ф. тождественно совпадает с ф. 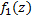 в области
в области 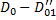 и с
и с 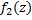 в области
в области 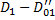 . Ф.
. Ф. 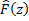 может быть аналитически продолжена на множество
может быть аналитически продолжена на множество 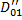 двумя способами:
двумя способами: 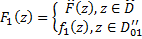 или
или 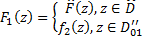 .
.
Это приводит к необходимости рассмотрения многозначной аналитической ф. 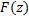 , определённой в области
, определённой в области 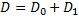 и принимающей различные значения в одних и тех же точках части
и принимающей различные значения в одних и тех же точках части 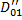 области
области 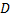 . В частности, получаем двухзначную аналитическую ф.
. В частности, получаем двухзначную аналитическую ф. 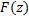 , принимающую в одной и той же т.
, принимающую в одной и той же т. 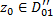 два различных значения, совпадающие со знач. ф.
два различных значения, совпадающие со знач. ф. 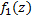 или
или 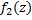 в этой т.
в этой т.
Работая с многозначной ф. 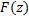 , встречаются трудности с выбором её значений в этой т. И для удобства пользуются понятием ветви аналитической ф. являющейся однозначной и непрерывной ф. в обл. опред. ф.
, встречаются трудности с выбором её значений в этой т. И для удобства пользуются понятием ветви аналитической ф. являющейся однозначной и непрерывной ф. в обл. опред. ф. 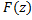 . Однако более удобным оказывается иное представление: будем рассматривать данную ф. как однозначную, но определённую на более сложном многообразии, чем обычная плоскость комплексной переменной.
. Однако более удобным оказывается иное представление: будем рассматривать данную ф. как однозначную, но определённую на более сложном многообразии, чем обычная плоскость комплексной переменной.
Будем считать, что обл. 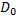 и
и 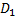 склеены по общей части
склеены по общей части 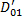 , в которой ф.
, в которой ф. 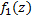 и
и 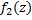 совпадают, а два экземпляра
совпадают, а два экземпляра 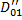 принадлежащие областям
принадлежащие областям 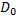 и
и 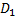 оставлены свободными. Тогда на полученном геометрическом многообразии, представляющем собой объединение областей
оставлены свободными. Тогда на полученном геометрическом многообразии, представляющем собой объединение областей 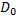 и
и 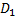 склеенных по
склеенных по 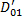 , ф.
, ф. 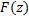 является однозначной аналитической ф.
является однозначной аналитической ф.
Построенное таким образом многообразие называется Римановой поверхностью аналитической ф. 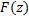 , являющейся аналит. продолжением ф.
, являющейся аналит. продолжением ф. 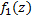 (или
(или 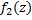 ), а отдельные экземпляры повторяющихся областей – различными листами римановой поверхности.
), а отдельные экземпляры повторяющихся областей – различными листами римановой поверхности.
Таким образом, вместо рассмотрения многозначной ф. на комплексной плоскости 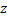 мы можем рассматривать однозначную ф. на Римановой поверхности.
мы можем рассматривать однозначную ф. на Римановой поверхности.
