Опр7. ( Собственный (несобственный) максимум (минимум) ф.)

Говорят, что ф. в т. имеет собственныймаксимум (минимум), если её можно окружить такой окрестностью: , чтобы для всех точек этой окрестности выполнялось неравенство: ( ). В противном случае имеем несобственный максимум (минимум).

Опр8. ( Необходимое условие существовании экстремума).

Если ф. в некоторой т. имеет экстремум, и если в этой т. 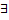конечные (частные) производные: , то все эти частные производные равны нулю.

Экстремум, как и в случае с ф. одной переменной, следует искать только в тех т., где . Такие точки называются стационарными.

Выпуклость и вогнутость функции.

Опр9 (выпуклость (вогнутость)).

Ф. , определена и непрерывная в промежутке Ω, называется выпуклой (выпуклой вниз), если для любых т. 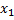и 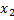из Ω выполняется неравенство: , каковы бы ни были положительные числа и , в сумме дающие единицу.

Ф. называется вогнутой (выпуклой вверх). если .

Свойства выпуклых функций.

1) Произведение выпуклой ф. на положительную постоянную есть выпуклая ф.

2) Сумма двух или нескольких выпуклых ф. тоже выпукла.

3) Если есть выпуклая и притом возрастающая ф., а также выпукла, то и сложная ф. будет выпуклой.

4) Есл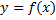и и 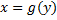однозначные взаимно обратные ф. (в соответствующих промежутках), то одновременно:

выпукла, возрастает выпукла, убывает вогнута, убывает	вогнута, возрастает выпукла, убывает вогнута, убывает

5)

Выпуклая в промежутке Ω ф. , отличная от постоянной, не может достигать наибольшего значения внутри этого промежутка.

6) Если промежуток , где , содержится в промежутке Ω, в котором ф. выпукла, то соотношением выполняется либо всегда со знаком равенства, либо всегда со знаком неравенства.

Условия выпуклости функции.

Т1. (Первая производная).

Пусть ф. определена и непрерывна в промежутке Ω и имеет в нем конечную производную . Для того, чтобы была выпуклой в Ω, необходимо и достаточно, чтобы её производная возрастала (в широком смысле).

Т2. (Вторая производная).

Пусть ф. определена и непрерывна вместе со своей производной в промежутке Ω и имеет внутри него конечную вторую производную . Для выпуклости ф. в Ω необходимо и достаточно, чтобы внутри Ω выполнялось: .

Т3. (Графический способ).

Пусть ф. определена и непрерывна в промежутке Ω и имеет в нем конечную производную . Для выпуклости ф. необходимо и достаточно, чтобы её график всеми точками лежал над своей касательной.

Точки перегиба.

Опр10 (Точка перегиба).

Т. кривой называют её точкой перегиба, если она отделяет участок кривой, где ф. выпукла (выпукла вниз), от участка, где эта ф. вогнута (выпукла вверх).

Асимптоты графика функции одной переменной.

Опр11 (Асимптота).

Пусть имеем кривую, ветвь которой в том или ином направлении удаляется в бесконечность. Если расстояние 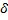от точки кривой до некоторой определённой прямой по мере удаления точки в бесконечность стремится к нулю, то эта пряма называется асимптотой кривой.