Т1. (Необходимое и достаточное условие дифф.-ти)

Для того чтобы ф. 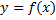являлась дифференцируемой в данной т. 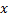, необходимо и достаточно, чтобы она имела в этой т. конечную производную.

Док-во:1)Необходимость. Пусть ф. 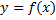дифф-ма в данной т. 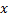, т.е. её приращение 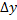в этой т. представимо в виде 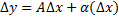. Предположив, что 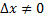и поделив это равенство на 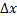, получим: 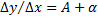. Из полученного равенства вытекает существование производной, т.е. предельного значения 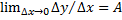. 2) Достаточность. Пусть ф. 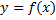имеет в данной т. 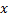конечную производную, т.е. 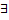предельное значение: 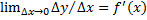. В силу определения предельного знач. ф.: 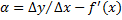аргумента 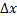является б.м. при 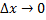, т.е. 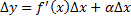, где . 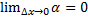Это представление совпадает с исходным, если обозначить через 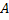не зависящее от 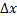число 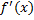. Ч.т.д.

Зам.:Т1 позволяет отождествлять понятие дифференцируемости ф. в данной т. с понятием существования у ф. в данной т. производной. Именно по этому операция нахождения производной называется дифференцированием.

Понятие дифференциала.

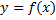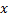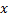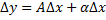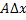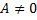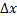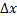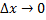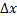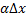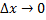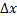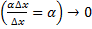Пусть ф. дифференцируема в т. , т.е. приращение этой ф. в т. может быть записано в виде: . Первое слагаемое при представляет собой функцию приращения аргумента , линейную и однородную относительно ; также оно представляет собой при б.м. такого же порядка, что и ; Второе слагаемое при является б.м. более высокого порядка, чем (т.к. при 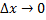). Таким образом, при 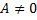первое слагаемое 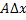является главной частью приращения дифф.-ой ф.

Сухой остаток: Дифференциалом функции называетсяглавная часть приращения дифференцируемой функции.

Производные высших порядков.

Понятие производной n– го порядка.

Производная 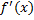ф. 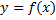, определённой и дифференцируемой на интервале 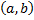, представляет собой ф., также определённую на интервале 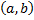. Может случится, что эта ф. 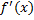сама является дифференцируемой в некоторой т. 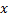интервала 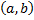, т.е. имеет в этой т. производную. Тогда указанную производную называют производной 2 – го порядка ф.

Обозначают так: , , , ,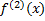

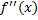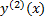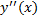После того как введено понятие второй произв., можно ввести понятие третей произв. и .т.д. Таким образом, понятие n – й произв. будет вводится индуктивно, переходя от перво к последующим.

Обозначают так: .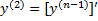

Что касается физ. смысла, если первая производная это скорость движущейся точки в момент времени 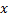, то вторая это скорость изменения скорости, т.е. ускорения точки.

Производные некоторых ф.

1) Степенной ф.

.

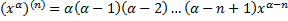2) Показательная ф.

.

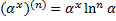3) n – я производная 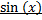(Аналогично )

.

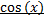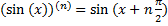4) Дробно – линейная ф.

.

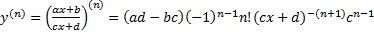5) Формула Лейбница для n – й производной произведения двух ф.

.

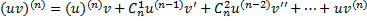Дифференциалы высших порядков.

Предположим, что ф. 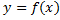дифференцируема в некоторой окрестности т. 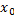. Тогда первый дифференциал 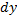этой ф. имеет вид 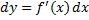и является ф. двух переменных: т. 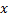и величины .

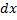Также предположим, что ф. 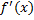также является дифференцируемой в т. 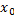и что вел. 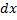имеет одно и тоже фикс. значение для всех точек 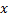рассматриваемой окрестности .

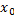При этих предположениях существует дифференциал ф. 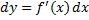в т. 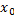, обозначаемый символом 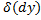, и определяемый формулой: .

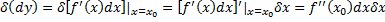Опр7 (Второй дифференциал).

Значение 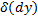дифференциала от первого дифференциала 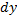, взятое при 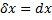, называют вторым дифференциалом ф. 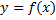( в т. 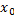) и обозначают символом .

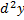Второй дифференциал записывают так: .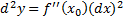

Аналогично, методом индукции, будут определяться дифференциалы высших порядков.

Дифференциал n– гопорядка записывают так: 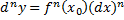.