Т5. (Сумма пред. равна пред. суммы)
Если каждое слагаемое алгебраической суммы ф. имеет пред. при  , то и алгеб. сумма имеет пред. при
, то и алгеб. сумма имеет пред. при  , причём пред. алгеб. суммы равен алгеб. сумме пред. т.е.
, причём пред. алгеб. суммы равен алгеб. сумме пред. т.е.
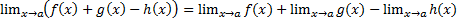 .
.
Т6. (Произведение под знаком предела).
Если каждый из сомножителей произведения конечного числа ф. имеет пред. при  , то и произв. имеет предел при
, то и произв. имеет предел при  , причём пред. произв. равен произведению пред. т.е.
, причём пред. произв. равен произведению пред. т.е.
 .
.
Т7. (Деление под знаком предела).
Если ф.  и
и 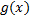 имеют предел при
имеют предел при  , причём
, причём 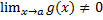 , то и их частное имеет предел при
, то и их частное имеет предел при  , причём предел частного равен частному пределов. т.е.
, причём предел частного равен частному пределов. т.е.
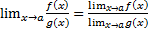 .
.
Замечательные пределы функции.
1) Первый замечательный предел.
Предельное значение ф. 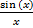 в точке
в точке 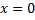 существует и равно единице. т.е.
существует и равно единице. т.е. 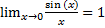 .
.
Второй замечательный предел.
Предельное значение ф. 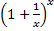 при
при  существует и равно e. т.е.
существует и равно e. т.е.
 .
.
Свойства эквивалентных бесконечно малых функций.
Опр6 ( б.м.ф.)
Ф. 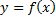 называется б.м. в т.
называется б.м. в т. 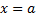 ( при
( при  ), если
), если 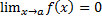 .
.
Зам.: Если ф. 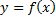 имеет равное
имеет равное 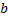 предельное значение в т.
предельное значение в т.  , то ф.
, то ф. 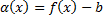 является б.м. в т.
является б.м. в т.  .
.
Опр7 (б.б. справа(слева))
Ф.  наз. б.б. в т.
наз. б.б. в т.  справа (слева), если для любой сход. к
справа (слева), если для любой сход. к  послед.
послед.  знач. аргумента
знач. аргумента 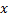 , элементы
, элементы 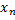 которой больше (меньше)
которой больше (меньше)  , соотв. послед.
, соотв. послед.  значений ф. являетсяб.б. послед определённого знака.
значений ф. являетсяб.б. послед определённого знака.
Обозначается так: 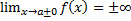 .
.
Сравнение б.м.ф.
Пусть 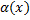 и
и 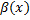 – две заданные на одном и том же мн-ве ф., являющиеся б.м. в т.
– две заданные на одном и том же мн-ве ф., являющиеся б.м. в т. 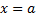 .
.
1) Ф. 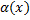 наз. б.м. более высокого порядка, чем
наз. б.м. более высокого порядка, чем 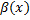 (имеет более высокий пор. малости), если пред. знач. ф.
(имеет более высокий пор. малости), если пред. знач. ф.  в т.
в т.  равно 0.
равно 0.
2) Ф. 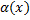 и
и 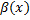 наз. б.м. одного порядка (имеют одинаковый порядок малости), если пред. знач. ф.
наз. б.м. одного порядка (имеют одинаковый порядок малости), если пред. знач. ф.  в т.
в т.  сущ. и
сущ. и 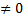 .
.
3) Ф. 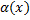 и
и 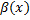 наз. эквивалентными б.м., если пред. знач. ф.
наз. эквивалентными б.м., если пред. знач. ф.  в т.
в т.  равно 1.
равно 1.
Свойства эквивалентных б.м.
1)  , и
, и  .
.
2) Если  и
и  , то
, то 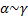 , и
, и 
3) Если  и
и  , то
, то  .
.
4) Если 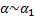 и
и 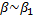 и
и 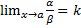 , то и
, то и 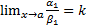 или
или 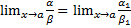 .
.
4-е свойство самое важное, т.к. на практике это означает, что предел отношения б.м. не меняется при замене их на эквивалентные б.м.
Непрерывность функции одной и нескольких переменных.
Свойства функций, непрерывных в точке и на отрезке. Равномерная непрерывность. Классификация точек разрыва.
Непрерывность функции одной и нескольких переменных.
Пусть т. 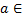 области задания ф.
области задания ф.  и
и 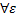 – окрестность т.
– окрестность т.  содержит отличные от
содержит отличные от  точки области задания этой ф.
точки области задания этой ф.
Опр1 (Непр. ф. одной пер.)
Ф.  называется непрерывной в т.
называется непрерывной в т.  , если предельное знач. этой ф. в т.
, если предельное знач. этой ф. в т. 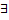 и равно частному значению
и равно частному значению 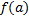 .
.
Обозначается так: 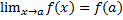 .
.
Опр2 (Непр. ф. неск. пер.)
Ф.  называется непрерывной в т.
называется непрерывной в т.  , если для
, если для 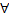 сход. к
сход. к  послед.
послед.  знач. аргумента
знач. аргумента 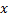 соответствующая послед.
соответствующая послед.  значений этой ф. сход. к числу
значений этой ф. сход. к числу 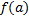 .
.
Опр3 (Непр. ф. справа (слева)).
Ф.  наз. непрерывной справа (слева) в т.
наз. непрерывной справа (слева) в т.  , если правое (левое) предельное значение этой ф. в т.
, если правое (левое) предельное значение этой ф. в т.  и равно частному значению
и равно частному значению 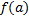 .
.
Обозначается так:
Справа: 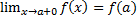 или
или  .
.
Слева: 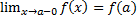 или
или 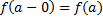 .
.
Зам.:Если ф.  непрерывна в точке
непрерывна в точке  и слева и справа, то она непрерывна в этой точке.
и слева и справа, то она непрерывна в этой точке.
Опр4 (Сложная ф.)
Ф., образованные в результате суперпозиции (т.е. последовательного применения) двух или неск. ф., будем наз. сложными.
Пусть ф. 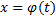 задана на некотором мн-ве
задана на некотором мн-ве 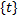 , и пусть
, и пусть 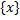 – множество знач. этой ф.
– множество знач. этой ф.
Предположим, что на указанном мн-ве 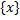 определена другая ф.
определена другая ф. 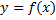 . Тогда, на мн-ве
. Тогда, на мн-ве 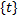 задана сложная ф.:
задана сложная ф.: 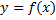 где
где 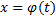 .
.
Обозначается так: 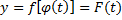 .
.
Опр5 (Непр. сложной ф.)
Если ф. 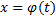 непр. в т.
непр. в т.  , а ф.
, а ф. 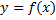 непр. в соотв. т.
непр. в соотв. т. 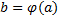 , то сложная ф.
, то сложная ф. 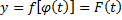 непр. в т.
непр. в т.  .
.
Опр6 (огр. сверху (снизу)).
Ф.  наз. ограниченной сверху (снизу) на мн-ве
наз. ограниченной сверху (снизу) на мн-ве 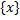 , если найдётся такое вещественное число
, если найдётся такое вещественное число 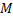 (число
(число 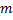 ), что для всех значений арг.
), что для всех значений арг. 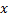 из мн-ва
из мн-ва 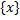 справедливо нерав.:
справедливо нерав.: 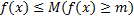 . При этом число
. При этом число 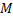 (число
(число 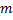 ) называется верхней (нижней) гранью ф.
) называется верхней (нижней) гранью ф.  на мн-ве
на мн-ве 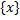 .
.
