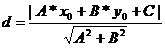Параметрическое уравнение прямой в плоскости.

Уравнение вида 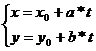- параметрическое уравнение прямой в плоскости.

Доказательство:

Для начала докажем, что любая точка прямой удовлетворяет .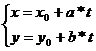

Проведем в плоскости прямую L, зададим на этой прямой точку Р с координатами (x,y) и вектор 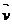, начинающийся в точке Р₀ с координатами (x0,y0), с координатами (a,b).

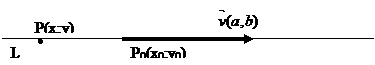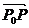=(x-x₀;y-y₀)

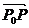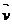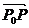// => =t*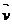

=>

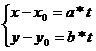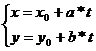
Теперь докажем, что любое решение системы является точкой принадлежащей L.

Теперь в отличие от первого случая возьмем точку Р с координатами (x,y), не принадлежащую прямой L.

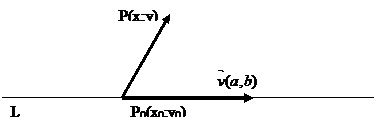Вектор 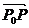не коллениарен вектору .

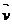Предположим, что для точки Р выполняется .=> => //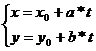

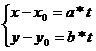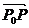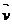
Противоречие => предположение неверно=> lдля точки не лежащей на прямой не выполняется.

=> система вида 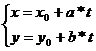, задаёт прямую.

Геометрический смысл параметрического уравнения прямой.

В системе 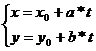x₀,y₀ – координаты некоторой точки на прямой, а a,b - координаты направляющего вектора.

Каноническое уравнение прямой в плоскости.

Уравнение вида 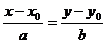называется каноническим уравнением прямой в плоскости.

Уравнение вида 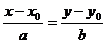задает прямую в плоскости.

Доказательство:

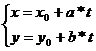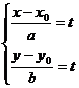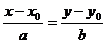=> => - каноническое уравнение прямой в плоскости.

В этом уравнение плоскости подразумевается не дробь, а отношение в котором снизу может быть ноль.

Геометрический смысл полностью следует из параметрического уравнения прямой.

Общее уравнение прямой.

Уравнение вида A*x + B*y + C=0 называется общим уравнением прямой.

Уравнение вида A*x + B*y + C=0 задает прямую в плоскости

Доказательство:

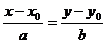=>b*(x-x₀)=a*(y-y₀)=>b*x – a*y + (a*y₀ - b*x₀)=0

Заменим b на A, -а на B, (a*y₀ - b*x₀) на С.

=> A*x + B*y + C=0.

Теорема

Уравнение A*x + B*y + C=0, где 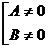, является уравнением прямой в плоскости с направляющим вектором (-В,А).

Доказательство:

Пусть (x₀,y₀) – решение уравнения, то есть A*x₀ + B*y₀ + C=0,

вычтем его из исходного уравнения,

получим: A*(x-x₀)+B*(y-y₀)=0 – полученное уравнение эквивалентно.

A*(x-x₀)=-B*(y-y₀)=> 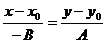- это уравнение прямой с направляющим вектором (-В,А).

Критерий коллинеарнности вектора прямой.

Вектор 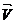с координатами (a,b) будет коллинеарен прямой L: A*x + B*y + C=0 тогда, и только тогда, когда A*a+B*b=0.

Доказательство:

Пусть точка P₀ с координатами (x_0,y₀) принадлежит прямой L.

(=>)Приложим вектор 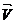к точке P₀. => P₁=( x₀+a, y₀+b)

=> A*(x₀+a) B*(y₀+b)+C=0 => A*x₀ + A*a + B*y₀ + B*b+C=0

A*a + B*b + (A*x₀ + B*y₀ + C)=0, A*x₀ + B*y₀ + C=0 т.к. P₁ принадлежит L

=> A*a+B*b=0

(<=) не дано надо стрясти.

Все сказанное относится к произвольной аффинной системе координат.

Геометрический смысл коэффициентов.

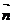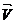( , )=A*B – B*A=0

В прямоугольной системе координат (А;В) – координаты вектора нормали.

Расстояние от точки до прямой в плоскости.

Пусть прямая L задана общим уравнением прямой, координаты точки Р=(x_0,y₀).

Тогда расстояние(d(P,L)) равняется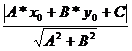

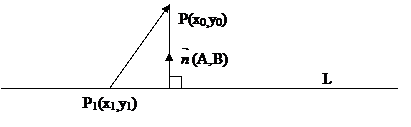
Доказательство:

Возьмем точку P₁ c координатами (x₁;y₁), лежащую на прямой L.

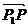=(x₀-x₁;y₀-y₁), 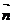=(A,B)

=

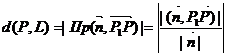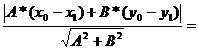
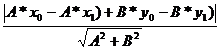
A*x₁ + B*y₁ + C=0 =>С= -A*x₁ - B*y₁

=>